Interférences,
trous d'Young, bac Asie Pacifique 2022.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
.
.
|
..
..
......
...
|
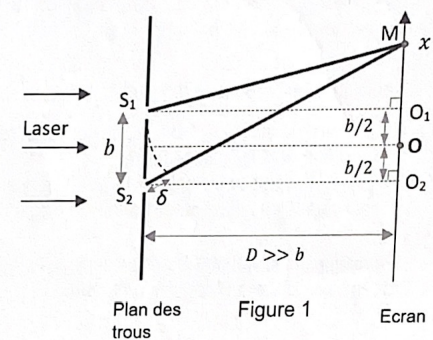
Relation entre interfrange et longueur d'onde.
1. Justifier que la différence de marche d peut être assimilée à S2M-S1M dans le cas où le milieu est l'air.
L'indice de réfractiondu milieu, l'air ,est n = 1.
2. Donner les expressions de S1M2 et S2M2 en fonction de D, x et ½b.
Triangle rectangle S1O1M : S1M2 =D2 +(x-½b)2.
Triangle rectangle S2O2M : S2M2 =D2 +(x+½b)2.
D >> b alors S2M2 -S1M2 = 2 D d.
3. En déduire que d =x b / D.
S2M2 -S1M2 =(x+½b)2 -(x-½b)2 =2bx.
2bx. =2 D d.
d =x b / D.
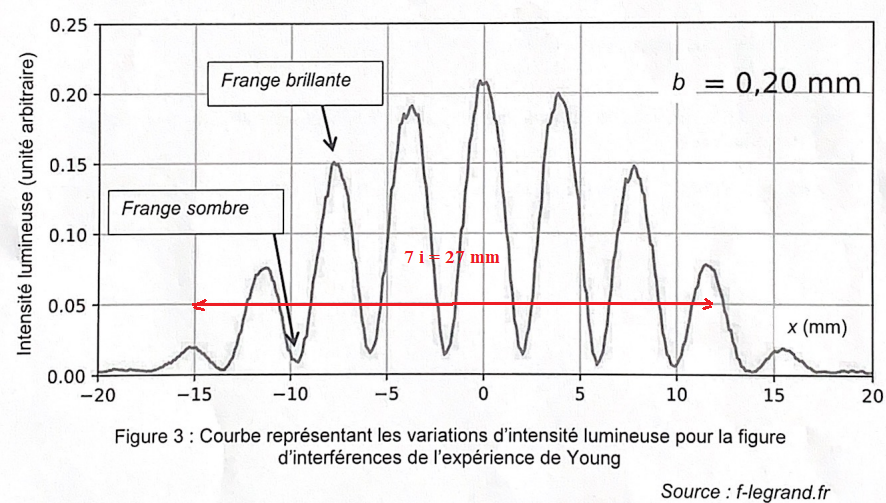
La figure suivante représente la figure d'interférences obtenue :
4. Montrer que x = k l D / b pour un point M situé au maximum d'intensité d'une frange brillante.
Interférences constructives d = k l.
k l = x b / D.
x = k l D / b.
5. Etablir l'expression de l'interfrange , notée i, distance entre deux franges de même nature consécutive.
k = 0 ; x = 0 ; k = 1 : x 1 = l D / b.
i = x1-0 = l D / b.
6. Déterminer précisément i à l'aide de la figure.
7 i = 27 mm ; i =3,9 mm.
7. En déduire la longueur d'onde de ce laser.
b = (2,0 ±0,1 )10-4 m. D = (119,0 ±0,5) cm.
l = i b / D=3,9 10-3 x 2,0 10-4 / 1,19 =6,6 10-7 m = 6,6 102 nm..
On considère que u(i) = 0,1 nm.
Incertitude sur l : u(l) = l [(u(b) / b)2+(u(i) / i)2+ (u(D) / D)2]½ .
u(l)= 6,6 102 [(0,1 /2 )2+(0,1 / 3,9)2+ (0,5) / 119)2]½ = 6,6 102 x 0,056 ~37 nm.
l = (6,6 102 ± 37) nm soit [ 623 ; 697 nm ]
Laser utilisés :
Rouge B ( 652 nm ; laser A rouge ( 632 nm ); laser rouge C ( 694 nm).
|
|