Mathématiques, géométrie dans l'espace, bac Nlle Calédonie 2022.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

.
. . .

.
.
.. ..
......


...
Une maison est constituée d’un parallélépipède rectangle ABCDEFGH surmonté d’un prisme
EFIHGJ dont une base est le triangle EIF isocèle en I.
Cette maison est représentée ci-dessous.

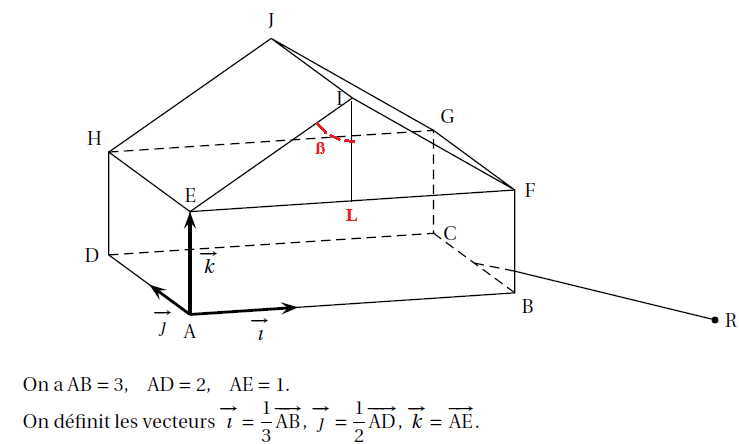1. Donner les coordonnées du point G.
G(3 ; 2 ; 1).
2. Le vecteur n de coordonnées (2 ; 0 ; −3) est vecteur normal au plan (EHI).
Déterminer une équation cartésienne du plan (EHI).
2x -3z+d = 0.
E(0 ; 0 ; 1) appartient à ce plan : 2xE -3zE+d = 0.
-3+d=0 ; d=3.
2x -3z+3 = 0.
3. Déterminer les coordonnées du point I.
Le triangle EIF est isocèle en I : xI = AB / 2 = 1,5.
I appartient à la façade avant de la maison : yI = 0.
I appartient au plan ( EHI ) : 2xI -3zI+3 = 0.
2 *1,5 -3zI +3 = 0 ; zI = 2.
I( 1,5 ; 0 ; 2).
4. Déterminer une mesure au degré près de l’angle EIF= 2 ß.
tan ß =EL / IL = 1,5 / 1 =2 ; ß ~56,3 ; 2 ß ~113°.
5. Afin de raccorder la maison au réseau électrique, on souhaite creuser une tranchée rectiligne depuis un relais électrique situé en contrebas de la maison.
Le relais est représenté par le point R de coordonnées (6 ; −3 ; −1).
La tranchée est assimilée à un segment d’une droite D passant par R et dirigée par levecteur u de coordonnées (−3 ; 4 ; 1). On souhaite vérifier que la tranchée atteindra la maison au niveau de l’arête [BC].
a. Donner une représentation paramétrique de la droite D.
x = -3t +xR =-3t+6.
y = 4t+yR = 4 t -3.
z = r+zR = t-1 avec t réel.
b. On admet qu’une équation du plan (BFG) est x = 3.
Soit K le point d’intersection de la droite D avec le plan (BFG).
Déterminer les coordonnées du point K.
K appartient au plan (BGF), donc xK = 3.
K appartient à la droite D : xK = 3=-3t+6 ; t =1.
yK = 4-3=1 ; zK =1-1=0.
K(3 ; 1 ; 0).
c. Le point K appartient-il bien à l’arête [BC] ?
 (xB+xC) / 2 =(3+3) / 2 = 3=xK.
 (yB+yC) / 2 =(0+2) / 2 = 1=yK.
 (zB+zC) / 2 =(0+0) / 2 = 0=zK.
K est le milieu du segment [BC].

...
....

 Une maison est modélisée par un parallélépipède rectangle ABCDEFGH surmonté d’unepyramide EFGHS.

1. Donner, sans justifier, les coordonnées des points B, E, F et G.
B(6 ; 4 ; 0) ; E(0 ; 4 ; 4) ; F(6 ; 4 ; 4) ; G(6 ; 0 ; 4).
2. Démontrer que le volume de la pyramide EFGHS représente le septième du volume total de la maison.
Volume du parallèlépipède : 4 x4 x6 = 96 m3.
Volume de la pyramide de base 24 m2 et de hauteur 2 m : 24 x2 / 3 = 16 m3.
Volume total : 96+16=112 m3.
16 /112=1 / 7.
3. a. Démontrer que le vecteur n de coordonnées(0 ; 1 ; 1)  est normal au plan (EFS).

b. En déduire qu’une équation cartésienne du plan (EFS) est y +z −8 = 0.
0 x +y + z +d = 0.
E(0 ; 4 ; 4 ) appartient à ce plan : yE + zE +d = 0.
4+4+d = 0 ; d = -8.
4. On installe une antenne sur le toit, représentée par le segment [PQ]. On dispose des
données suivantes :
● le point P appartient au plan (EFS) ;
● le point Q a pour coordonnées (2; 3; 5,5) ;
● la droite (PQ) est dirigée par le vecteur k .
a. Justifier qu’une représentation paramétrique de la droite (PQ) est :
x = 2 ; y = 3 ; z = 5,5+t (t ∈ R).
Le vecteur k( 0 ; 0 ; 1) est un vecteur directeur de cette droite et le point Q appartient à cette droite :
x = 0 t+xQ ; x = 2.
y = 0 t +yQ ; y = 3.
z = t +zQ = t +5,5.
b. En déduire les coordonnées du point P.
Le point P appartient au plan (EFS)  : yP+zP-8=0.
Le point P appartient à la droite (PQ) : xP = 2 ; yP = 3 ; zP = t+5,5.
3+t+5,5-8=0 ; t = -0,5.
P(2 ; 3 ; 5).
c. En déduire la longueur PQ de l’antenne.
PQ = [(2-2)2 +(3-3)2 +(5,5-5)2]½ =0,5.
Un oiseau vole en suivant une trajectoire modélisée par la droite D dont une représentation paramétrique est :
x = -4+6s ;
y = 7-4s ;
z = 2+4s avec s réel.
Déterminer la position relative des droites (PQ) et D.
Coordonnées d'un vecteur directeur de la droite (PQ) : (0 ; 0 ; 1).
Coordonnées d'un vecteur directeur de la droite (D) : (6 ; -4 ; 4).
Ces deux droites ne sont pas parallèles, elles sont donc sécantes.
L’oiseau va-t-il percuter l’antenne représentée par le segment [PQ] ?
Si l'oiseau percute l'antenne :
2 = -4+6s ; s =1.
7 -4s = 3.
2+4s =6 = t+5,5 soit t = 0,5.
Coordonnées du point de percussion ( point commun à ces deux droites) : (2 ; 3 ; 6).
Or P a pour côte z = 5 et Q a pour côte z = 5,5.
6 n'appartient pas à [5 ; 5,5], donc l'oiseau ne percute pas l'antenne ; il passe au dessus.


  
menu