Manoeuvres avec un gyropode, avertisseur sonore, bac Nlle Calédonie 2022. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... Un gyropode est un véhicule électrique monoplace constitué d’une plateforme munie de deux roues et d’un manche de conduite. L’objectif est d’étudier, de manière simplifiée, deux manoeuvres effectuées en conduisant un gyropode. La masse totale du système {gyropode et conducteur} a pour valeur 110 kg. Le conducteur d’un gyropode circule en ligne droite sur une grande place à la vitesse de 16 km·h-1. Avant de contourner une fontaine circulaire, il freine entre A et B, diminuant sa vitesse à 10 km·h-1 en 1,1 s. 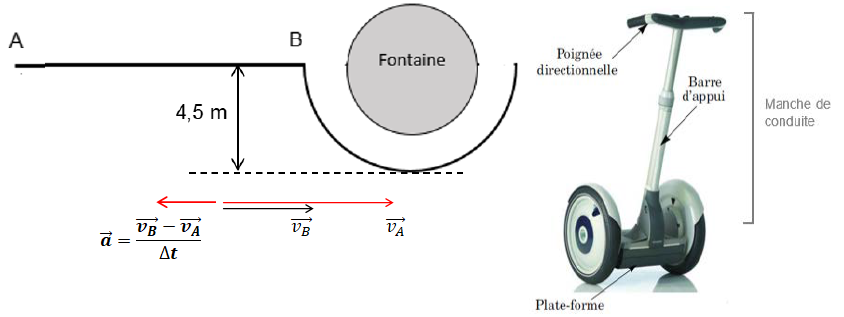Le vecteur accélération est considéré constant entre A et B. 1. Déterminer la direction et le sens du vecteur accélération entre A et B et montrer que sa valeur est environ 1,5 m·s-2. Le vecteur accélération est dirigé suivant  la droite (AB), de B vers A, de norme : a = (16 -10) / (3,6 x1,1) ~ 1,5 m·s-2. 2. Calculer la distance parcourue du point A au point B. Origines des temps et des distances : le point A. Sens de l'axe : A vers B. vA = 16 / 3,6 = 4,44 m /s. La vitesse est une primitive de l'accélération : v = at + vA = -1,5 t +4,44 ~ -1,5 t +4,4. La distance est une primitive de la vitesse : x = -½at2 +vAt = -0,75 t2 +4,4t. AB = -0,75 x1,12 +4,4 x1,1 ~ 4,0 m. On note FT l’ensemble des forces de frottement considéré constant quelle que soit la masse du conducteur et de ses équipements, et ceci durant la totalité de la phase de freinage entre A et B. 3. Déterminer, en détaillant le raisonnement, la valeur FT . L'énergie mécanique du système diminue du travail de la force de frottement. L'énergie mécanique est sous forme d'énergie cinétique. ½m vB2 -½m vA2 = - FT AB. vA = 16 / 3,6 =4,44 m /s ; vB = 10 / 3,6 =2,78 m /s. FT  =0,5 m(vA2 -vB2 ) / AB =55 x(4,442 -2,782) / 4,0 ~1,6 102  N. 4. À l’aide de la deuxième loi de Newton, discuter l’efficacité du freinage entre A et B si le conducteur avait porté un sac à dos de 10 kg, les forces de frottements n’ayant pas varié. Aucun calcul n’est attendu. Ecrire la seconde loi de Newton selon AB  ( le poids et l'action du plan se compensent) : -FT = m a ; a = - FT / m ; La valeur de l'accélaration diminue si FT reste constant  et si la masse augmente. La vitesse en B sera supérieure à 10 km / h : le freinage est moins efficace. Le conducteur cherche à contourner la fontaine en faisant un mouvement circulaire à la vitesse constante de 10 km·h-1. 5. Justifier l’existence d’un vecteur accélération du système alors que la valeur de la vitesse reste constante et donner les caractéristiques de ce vecteur accélération en précisant sa direction, son sens et sa valeur. La direction du vecteur vitesse change, donc il existe un vecteur accélération non nul. 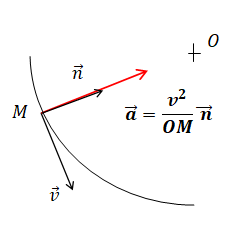a =v2 / OM =2,782 / 4,5 = 1,7 m s-2. Lors d’un mouvement circulaire avec ce gyropode, l’accélération ne doit pas dépasser 2,5 m.s-2 pour éviter tout basculement. 6. Préciser, en présentant un raisonnement, si le freinage entre A et B était nécessaire pour éviter un basculement. En absence de freinage entre A et B, v = 4,44 m /s et a = 4,442 / 4,5 = 4,4 m s-2. Valeur supérieure à 2,5 m s-2, en absence de freinage entre A et B, le gyropode bascule. ... .... Un gyropode, véhicule électrique monospace, est équipé d’un avertisseur capable d’émettre un signal sonore de fréquence 500 Hz et d’une puissance sonore de 80 mW. Lors de son utilisation, le niveau d’intensité sonore mesuré à 1,0 m devant le véhicule est de 100 dB. 1. Expliquer sans calcul ni formalisme mathématique l’origine de l’atténuation du niveau d’intensité sonore si la distance entre la source et l’émetteur augmente. Un schéma d’illustration simple est attendu. Pour une source ponctuelle, la puissance acoustique se répartit sur une surface sphérique. Si la distance de la source au récepteur croît, la surface de la sphère augmente. L'intensité sonore décroît avec le carré de la distance. 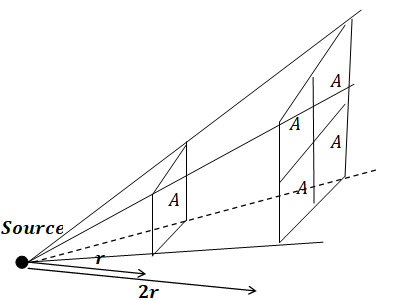Dans le cas d’une source sonore omnidirective (qui émet la même énergie dans toutes les directions), l’intensité sonore I à la distance d de la source est I = P / (4 p d2) où P est la puissance sonore de la source. 2. Calculer la puissance sonore associée à un niveau sonore de 100 dB à 1,0 m d’une source omnidirective. En déduire si l’avertisseur étudié est une source omnidirective. I = I0 1010 =10-12 x 1010 = 10-2 W m-2. P = 4 p d2 I = 4 x3,14 x12 x10-2 ~0,13 W= 1,3 102 mW. Cette valeur diffère de 80 mW. L'avertisseur n'est pas omnidirectif. Un promeneur, de dos par rapport au véhicule, écoute, avec un casque, de la musique à un niveau sonore de 85 dB. Il marche sur la chaussée quand le conducteur actionne l’avertisseur pour prévenir de son arrivée. On considère que l’intensité sonore due à l’avertisseur qui parvient aux oreilles du promeneur est de 8,0 × 10-5 W·m-2. Données : on admet qu’un son n’est pas perceptible par rapport à un autre si la valeur absolue de la différence de leurs niveaux d’intensité sonore est supérieure ou égale à 6 dB. 3. Déterminer si le promeneur entend distinctement le signal émis par l’avertisseur sonore. Niveau sonore du à l'avertisseur : L = 10 log ( 8,0 10-5 / 10-12) =79 dB. 85-79 = 6 dB, le promeneur entend distinctement le son de l'avertisseur. 4. Une personne située dans un bâtiment fermé à proximité n’entend pas du tout l’avertisseur sonore. Expliquer brièvement, en utilisant un vocabulaire scientifique rigoureux, le type d’atténuation mis en jeu. Les ondes acoustiques sont en partie réfléchies par le mur et en partie transmises à travers le mur. Si le mur est constitué d'isolant acoustique, la pesronne située dans le bâtiment fermé ne perçoit auncun son. Une autre personne située dans le même bâtiment entend très distinctement l’avertisseur sonore. Sa position dans la pièce est indiquée sur le schéma ci-dessous : 5. Nommer le phénomène physique qui intervient à travers l’ouverture et, à l’aide d’un calcul, justifier qu’il se produit. 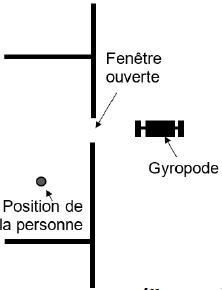Longueur d'onde du son de fréquence 500 Hz se propageant à la célérité c = 340 m /s.  l = c / f = 340 / 500 =0,68 m. La longueur d'onde est proche des dimensions des ouvertures du bâtiment. Le son sera donc diffracté par les ouvertures.

menu