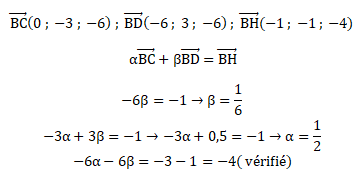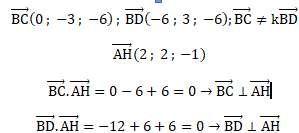L’espace
est muni d’un repère orthonormé .
On considère les points A(5 ; 0 ; −1), B(1 ; 4 ; −1), C(1; 0; 3),
D(5; 4; 3) et E(10; 9; 8).
1. a. Soit R le milieu du
segment [AB].
Calculer les coordonnées du point R ainsi que les coordonnées du
vecteur AB.
x
R= (x
A+x
B) / 2 = (5+1) / 2=3.
yR=
(yA+yB) / 2 = (0+4) / 2=2.
zR=
(zA+zB) / 2 = (-1-1) / 2= -1.
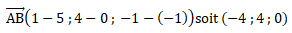
b. Ce
vecteur AB est normal au plan P
1 et E appartient à ce plan.
Donner l'équation cartésienne de ce plan.
-4x +4y +d = 0.
R(3 ; 2 ; -1) appartient à ce plan :
-4*3+4*2+d= 0 ; d = 4.
-4x +4y
+4 = 0 ou encore x-y-1=0.
c. Démontrer que
le point E(10 ; 9 ; 8) appartient au plan P
1 et que EA = EB.
x
E-y
E-1 =10-9-1 =0 est bien vérifiée, donc E
appartient au plan P
1.
EA= [(5-10)
2+(0-9)
2+(-1-8)
2]
½
=187
½.
EB= [(1-10)2+(4-9)2+(-1-8)2]½
=187½.
2. On considère le
plan P
2 d’équation cartésienne x − z −2 = 0.
a. Justifier que les
plans P
1 et P
2 sont sécants.
Coordonnées d'un vecteur normal à P
1 : (1 ; -1 ; 0).
Coordonnées
d'un vecteur normal à P2 : (1 ;0 ; -1).
Ces deux vecteurs n'étant pas colinéaires, les deux plans ne sont pas
parallèles.
b. On
note
D la droite
d’intersection de P
1 et P
2.
Démontrer qu’une représentation paramétrique de cette droite est
:
x = 2+ t
; y = 1+ t
; z = t
(t ∈ R).
Soit M(x, y z) un point de cette droite.
Si M appartient au plan P
1 : 2+t-1-t-1=0 est vérifiée quel
que soit t.
Si M appartient
au plan P2 : 2+t-t-2=0 est vérifiée quel que soit t.
Donc D est l’intersection de P1
et P2.
3. On considère le plan P
3
d’équation cartésienne y + z −3 = 0.
Justifier que la droite
D
est sécante au plan P
3 en un point
W dont on déterminera les
coordonnées.
Si la
droite D
est sécante au plan P3 , alors :
1+t+t-3 =0 ; t =1.
Coordonnées de W
: x = 2+t = 2+1 =3 ; y = 1+t = 1+1 = 2 ; z =t=1.
Si S et T sont deux points distincts de
l’espace, on rappelle que l’ensemble des points M de l’espace
tels que MS = MT est un plan, appelé plan médiateur du segment [ST]. On
admet que les plans P
1,
P
2 et P
3 sont les plans médiateurs respectifs des
segments [AB], [AC] et [AD].
4. a. Justifier que
WA =
WB = WC = WD.
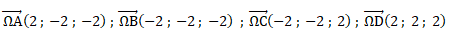
WA =[22+(-2)2+(-2)2
]½ =12½= 2*3½.
WB
=[(-2)2+(-2)2+(-2)2 ]½ =12½=
2*3½.
WC =[(-2)2+(-2)2+22
]½ =12½= 2*3½.
WD =[22+22+22
]½ =12½= 2*3½.
b. En
déduire que les points A, B, C et D appartiennent à une même sphère
dont on précisera
le centre et le rayon
W est équidistant de A, B, C
et D ; c'est le centre de la sphère de rayon 2*3
½.
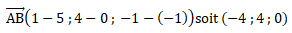
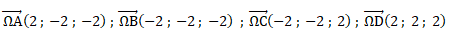
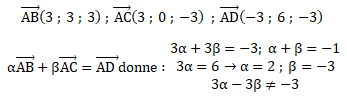
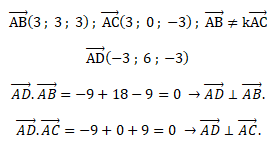
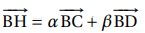 .
.