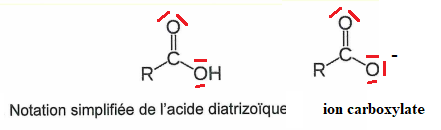
Dégradation d'un produit de contraste, bac Centres étrangers 2022. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . .. .. ...... ... Propriétés chimiques de l'acide diatrizoïque . Q1. Représenter le schéma de Lewis de cet acide et celui de l'ion carboxylate correspondant. Q2. Etablir l'équation de la réaction de cet acide avec l'eau et exprimer sa constante d'équilibre. RCOOH aq + H2O l = RCOO-aq +H3O+aq. Ka = [ RCOO-aq ]éq [H3O+aq ]éq / [ RCOOH aqéq]  Q3. Représenter le diagramme de prédominance de ce couple acide / base et identifier l'espèce prédominante dans les eaux usées ( pH compris entre 6,5 et 8). 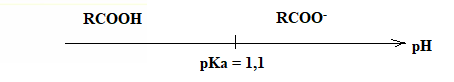A pH supérieur à pKa, la forme ion carboxylate prédomine. Cinétique de dégradation de produits de contraste. La figure suivante représente la variation de concentration des acides diatrizoïque etiotalamique en soutions aqueuse en fonction du temps. . 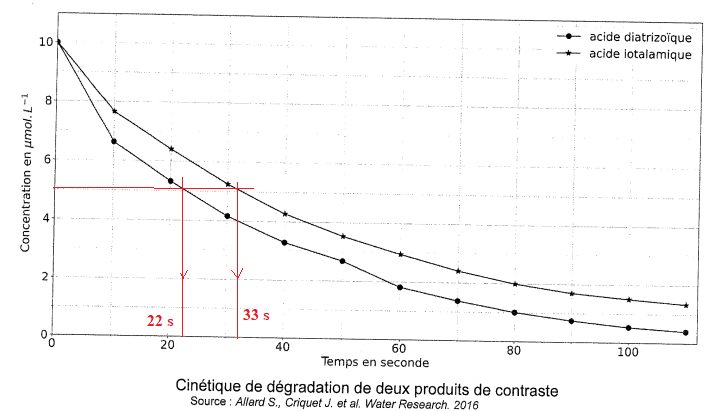Q4. Déterminer les temps de demi-réaction et indiquer le produit qui se dégrade le plus rapidement. L'acide diatrizoïque se dégrade plus rapidement que l'acide iotalamique. On s'intéresse à la dégradation de l'iopamidol en solution aqueuse. On note [Iop](t) la concentration de l'iopamidol à la date t. Q5. Donner la définition de la vitesse volumique de disparition de l'ioopamidol. v(t) = -d[Iop](t) / dt. Si cette cinétique est d'ordre 1, V s'écrit V = k [Iop](t) avec k une constante positive. Q6. En déduire que l'évolution temporelle de la concentration est modélisée par : d [Iop](t) / dt + k[Iop](t) =0. V = -d[Iop](t) / dt = k [Iop](t). D'où : d [Iop](t) / dt + k[Iop](t) =0. La solution de cette équation est de la forme : [Iop](t) = [Iop](0) exp(-kt). [Iop](0)=9,70 et k = 0,020. Q7. A partir de la courbe suivante, justifier que le modèle de cinétique d'ordre 1 est validé. 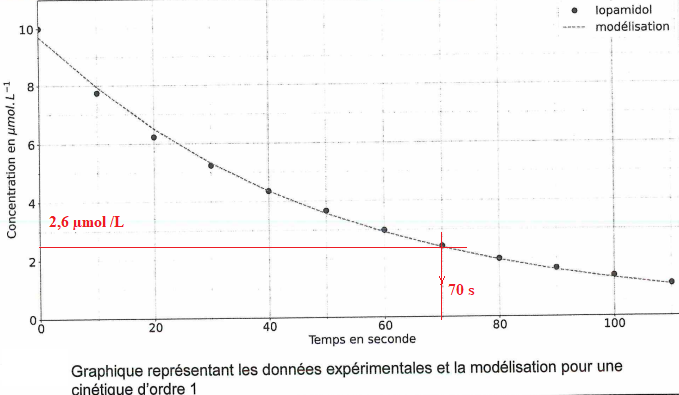Les points expérimentaux coincident avec le modèle cinétique d'ordre 1. Ce modèle est donc valide. Un établissement de santé souhaite traiter ses eaux usées à l'aide d'un rayonnement UV. La valeur de la concentration initiale en iopamidol est 10,0 µmol / L. Il souhaite de ne pas dépasser une concentration maximale de 2,0  mg / L pour l'eau traitée. Q8. Déterminer la durée minimum nécessaire au traitement. M(iopamidol) = 777 g / mol. 2,0 10-3 / 777 = 2,6 10-6 mol /L = 2,6 µmol / L. Le graphe donne 70 s.

menu