Mathématiques, suite, fonctions, Bac centres étrangers 2022. Arabie saoudite, Bahreïn, Chypre, Éthiopie, Grèce, Israël, Jordanie, Koweït, Qatar, Roumanie et Turquie En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... 1. Un récipient contenant initialement 1 litre d’eau est laissé au soleil. Toutes les heures, le volume d’eau diminue de 15 %. Au bout de quel nombre entier d’heures le volume d’eau devient-il inférieur à un quart de litre ?  a. 2 heures ; b. 8 heures ;  c. 9 heures  ; d. 13 heures. Volume restant au bout d'une heure : 0,85 litre. Au bout de n heures, volume restant 0,85n. 0,85n <0,25. n ln(0,85) < ln(0,25) ; -0,1635 n < -1,386 ; n > 8,47 soit n > 9 heures.  2. On considère la fonction f définie sur l’intervalle ]0 ; +∞[ par f (x) = 4ln(3x). Pour tout réel x de l’intervalle ]0 ; +∞[ , on a : a. f (2x) = f (x)+ln(24)−ln(1,5) ;  b. f (2x) = f (x)+ln(16) ;  c. f (2x) = ln(2)+ f (x) ; d. f (2x) = 2f (x). f(2x) = 4 ln(6x) = 4 ( ln(3x) +ln(2)) = f(x) +4 ln(2) =f(x) + ln(24) =f(x) + ln(16).  3. On considère la fonction g définie sur l’intervalle ]1 ; +∞[ par : g(x) = ln(x) /( x −1) . On note Cg la courbe représentative de la fonction g dans un repère orthogonal. La courbe Cg admet : a. une asymptote verticale et une asymptote horizontale.  b. une asymptote verticale et aucune asymptote horizontale.  c. aucune asymptote verticale et une asymptote horizontale.  d. aucune asymptote verticale .et aucune asymptote horizontale. g(x) = ln(x) / x * x / (x-1). Quand x tend vers plus l'infini : ln(x) / x tend vers zéro et x/(x-1) tend vers 1.  g(x) tend vers zéro et l'axe des abscisses est asymptote.  g(x) =  [ ln(x) -ln(1) ] / (x-1). Quand x tend vers 1+ : [ ln(x) -ln(1) ] / (x-1) tend vers la dérivée de ln(x) soit vers 1/x, c'est à dire 1. Il n'y a pas d'asymptote au voisinage de 1.  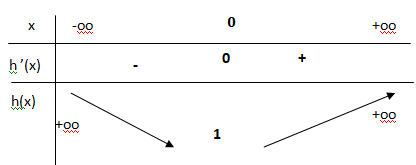Dans la suite de l’exercice, on considère la fonction h définie sur l’intervalle ]0; 2] par : h(x) = x2 (1+2ln(x)). On note Ch la courbe représentative de h dans un repère du plan. On admet que h est deux fois dérivable sur l’intervalle ]0; 2]. On note h ′ sa dérivée et h ′′ sa dérivée seconde. On admet que, pour tout réel x de l’intervalle ]0; 2], on a : h ′ (x) = 4x(1+ln(x)).  4. Sur l’intervalle ]1 /e ; 2] , la fonction h s’annule : a. exactement 0 fois ; b. exactement 1 fois ; c. exactement 2 fois ; d. exactement 3 fois. x2 (1+2ln(x)) = 0 soit x = 0 ( n'appartient pas à l'intervalle ]0; 2] et 1+2ln(x) =0 ; ln(x) = -0,5 ; x = e-0,5.  5. Une équation de la tangente à Ch au point d’abscisse e½ est : a. y =  6e0,5.x  ; b. y = 6e0,5.x +2e  ; c. y = 6e0,5 ; d. y = 6e0,5.x−4e. Coefficient directeur de la tangente : h ′ (e½) = 4e½(1+ln(e½))= 4e½(1+0,5)=6 e½. Le point de coordonnées (e½; f(e½)=e(1+2*0,5)=2e appartient à la tangente. Equation de la tangente : y = 6e½ x +b. 2e = 6e +b ; b = -4e. 6. Sur l’intervalle ]0; 2], le nombre de points d’inflexion de la courbe Ch est égal à : a. 0 ; b. 1 ; c. 2 ; d. 3. h ′ (x) = 4x(1+ln(x)). Calcul de h"(x) en posant u = 4x et v = 1+ln(x). u' = 4 ; v' = 1 /x. u'v+v'u = 4(1+ln(x) +4 = 4(2+ln(x)). h"(x) s'annule et change de signe pour ln(x) = -2 soit x = e-2.  7. On considère la suite (un) définie pour tout entier naturel n par un+1 = 0,5 un +3 et u0 = 6. On peut affirmer que : a. la suite (un) est strictement croissante. b. la suite (un) est strictement décroissante. c. la suite (un) n’est pas monotone. d. la suite (un) est constante. u1 = 6 ; u2 =6.... . Suite et fonction exponentielle. Partie A. On considère la fonction f définie pour tout réel x par : f (x) = 1+ x −e 0,5x−2 . On admet que la fonction f est dérivable sur R. On note f ′ sa dérivée. 1. a. Déterminer la limite de la fonction f en −∞. Le terme en exponentielle tend vers zéro et f(x) tend vers moins l'infini.  b. Démontrer que, pour tout réel x non nul, f (x) = 1+0,5x [ 2− e 0,5x/ 0,5x *e −2 ] . En déduire la limite de la fonction f en +∞. f(x) = 1+0,5x[ 2 -e0,5x-2 / 0,5x] . e0,5x-2  =e0,5x *e-2 ; par suite f (x) = 1+0,5x [ 2− e 0,5x/ 0,5x *e −2 ]. En plus l'infini, par croissance comparée : e 0,5x/ 0,5x tend vers plus l'infini. 2− e 0,5x/ 0,5x *e −2 tend vers moins l'infini. Par produit des limites, f(x) tend vers moins l'infini.  2. a. Déterminer f ′ (x) pour tout réel x. f '(x) = 1 −0,5 e 0,5x−2 .  b. Démontrer que l’ensemble des solutions de l’inéquation f ′ (x) < 0 est l’intervalle ]4+2ln(2) ; +∞[. 1 −0,5 e 0,5x−2 < 0 ; e 0,5x−2 > 2 ; 0,5x-2 > ln(2) ; 0,5x > ln(2)+2 ; x > 4 + 2ln(2). 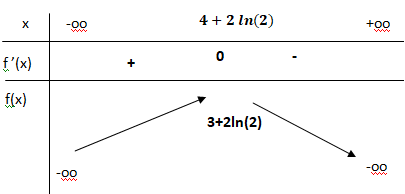3. Déduire des questions précédentes le tableau de variation de la fonction f sur R. On fera figurer la valeur exacte de l’image de 4+2ln(2) par f . f(4+2ln(2))=1+4+2 ln(2)- exp(2+ln(2)-2)=5+2ln(2)-2 = 3+2ln(2). 4. Montrer que l’équation f (x) = 0 admet une unique solution sur l’intervalle [−1 ; 0]. Sur cet intervalle, la fonction est strictement croissante de -e-2,5 ~-0,082 à 1-e-2 ~0,86. La fonction étant continue et dérivable, le théorème des valeurs intermédiaires indique qu'il existe une unique solution a sur [-1 ; 0] tel que f (a) =0.  Partie B On considère la suite (un) définie par u0 = 0 et, pour tout entier naturel n, un+1 = f (un) où f est la fonction définie à la partie A. 1. a. Démontrer par récurrence que, pour tout entier naturel n, on a : un < un+1 < 4. Initialisation : u0 = 0 ; u1 = f(0) =1-e-2 < 4. La propriété est vraie au rang 0. Hérédité : un < un+1 < 4 est supposée vraie. Sur [0 ; 4], la fonction f(x) est croissante, donc : f (un ) < f(un+1 )< f( 4) avec f(4) =4. un+1 < un+2 < 4. La propriété est vraie au rang n+1. Conclusion : la propriété est vraie au rang zéro et héréditaire, elle est vraie pour tout n entier naturel. b. En déduire que la suite (un) converge. On notera l la limite. La suite est croissante et majorée par 4, donc elle converge. 2. a. On rappelle que f vérifie la relation l= f (l). Démontrer que l = 4. l = 1+ l −e 0,5l−2 . 1=e 0,5l−2 ; ln(1) = 0,5 l-2 ;2 = 0,5 l ; l = 4. b. On considère la fonction valeur écrite cicontre dans le langage Python : def valeur (a) :  u = 0 n = 0  while u < a: u=1 + u - exp(0.5*u - 2)  n = n+1  return n  L’instruction valeur(3.99) renvoie la valeur 12. Interpréter ce résultat dans le contexte de l’exercice. L'algorithme calcule les premiers termes de cette suite jusqu'à celui qui est supérieur à 3,99. u12 est le premier terme supérieur à 3,99. ... .... 1. On considère la fonction f définie pour tout réel x par f (x) = ln ( 1+ x2 ) . Sur R, l’équation f (x) = 2022.  a. n’admet aucune solution ; b. admet exactement une solution ;  c. admet exactement deux solutions ;  d. admet une infinité de solutions. 2022 = ln(1+x2) ; e2022 = 1+x2 ; x2 = e2022-1. x = ±(e2022-1)½.  2. Soit la fonction g définie pour tout réel x strictement positif par : g(x) = x ln(x)− x2 . On note Cg sa courbe représentative dans un repère du plan.  a. La fonction g est convexe sur ]0 ; +∞[ . b. La fonction g est concave sur ]0 ; +∞[ .  c. La courbe Cg admet exactement un point d’inflexion sur ]0 ; +∞[. d. La courbe Cg admet exactement deux points d’inflexion sur ]0 ; +∞[. Calcul de la dérivée de x ln(x) : u = x ; v = ln(x) ; u' = 1 ; v' = 1 / x ; u'v+v'u =ln(x) +1. g'(x) = 1 +ln(x) -2x. g"(x) = 1 /x-2 = (1-2x) / x. g"(x) s'annule et change de signe pour x = 0,5.  3. On considère la fonction f définie sur ]−1 ; 1[ par f (x) = x / (1− x2). Une primitive de la fonction f est la fonction g définie sur l’intervalle ]−1 ; 1[ par : a. g(x) = − 1/ 2 ln( 1− x 2) ;  b. g(x) = 1+ x 2 / ( 1− x 2)2 ;  c. g(x) =0,5 x2/ (x-x3/3) ;  d. g(x) = x 2 /2 ln( 1− x 2 ). On dérive -0,5  ln( 1− x 2) : -0,5(-2x) /(1− x 2) = x / (1− x2). 4. La fonction f(x)= ln( −x 2 − x +6 ) est définie sur  a. ]−3 ; 2[  ; b. ]−∞ ; 6] ; c. ]0 ; +∞[; d. ]2 ; +∞[. −x 2 − x +6 > 0 ; discrilinant D =(-1)2 -4 (-1)*6 =25 = 52. x1 = (1 +5) / (-2) = -3 ; x2 = (1 -5) / (-2) =2. f(x) est définie sur ]−3 ; 2[. 5. On considère la fonction f définie sur ]0,5 ; +∞[ par f (x) = x 2 −4x +3ln(2x −1). Une équation de la tangente à la courbe représentative de f au point d’abscisse 1 est : a. y = 4x −7  ; b.  y = 2x −4;  c. y = −3(x −1)+4;  d. y = 2x −1. f '(x) = 2x-4+6/(2x-1). f '(1) =2-4+6 =4. Equation de la tangente : y = 4x+b. Le point de coordonnées (1 ; f(1) =-3) appartient à la tangente : -3 = 4 +b ; b = -7. 6. L’ensemble S des solutions dans R de l’inéquation ln(x +3) < 2ln(x +1) est :  a. S =]−∞ ; −2[∪]1 ; +∞[ ; b. S =]1 ; +∞[ ; c. S aucune solution ;  ; d. S =]−1 ; 1[.  x doit être strictement supérieur à -1. ln(x +3) < ln(x +1)2 ; x+3 < (x+1)2. x+3 < 1+2x+x2. x2+x-2 >0. D =12-4(-2) =9=32. x1 = (-1+3) / 2 =1 ; x2 = (-1-3) / 2 =-2. x appartient à ]-oo ; -2[ union ]1 : +oo[. Fonction exponentielle et suite. Partie A : Soit h la fonction définie sur R par h(x) = e x − x.  1. Déterminer les limites de h en −∞ et +∞. h(x) = ex(1-x / ex). En plus l'infini, par croissance comparée x / ex tend vers zéro et h(x) tend vers plus l'infini. En moins l'infini, ex tend vers zéro et h(x) tend vers plus l'infini.  2. Étudier les variations de h et dresser son tableau de variation. h'(x) = ex-1 s'annule pour x =0. h'(x) >0 si x >0 ; h(x) est croissante. h'(x) <0 si x <0 ; h(x) est décroissante.  3. En déduire que : si a et b sont deux réels tels que 0 < a < b alors h(a)−h(b) < 0. Sur R+, h(x) est strictement croissante. si 0 < a < b alors h(a)<h(b) . Or h(0) = 1, donc 1 < h(a) < h(b) soit h(a)−h(b) < 0.  Partie B : Soit f la fonction définie sur R par f (x) = e x .On note Cf sa courbe représentative dans un repère orthonormé. 1. Déterminer une équation de la tangente T à Cf au point d’abscisse 0. f '(x) = ex ; f '(0) = 1. Equation de la tangente y = x+b. Le point de coordonnées (0 ; f(0) =1) appartient à la tangente. 1 = 0+b ; b =1. y = x+1. Dans la suite de l’exercice on s’intéresse à l’écart entre T et Cf au voisinage de 0. Cet écart est défini comme la différence des ordonnées des points de T et Cf de même abscisse. On s’intéresse aux points d’abscisse 1/ n , avec n entier naturel non nul. On considère alors la suite (un) définie pour tout entier naturel non nul n par : un = exp( 1/ n) − 1/ n −1.  2. Déterminer la limite de la suite (un). Quand n tend vers plus l'infini : 1 /n tend vers zéro ; ex(1/n) tend vers1 et un tend vers zéro. 3. a. Démontrer que, pour tout entier naturel non nul n, un+1 −un = h (1 /( n +1))  −h ( 1/ n) où h est la fonction définie à la partie A. un+1 −un =exp( 1/ (n+1)) − 1/ (n+1) −1 -[exp( 1/ n) − 1/ n −1] =exp( 1/ (n+1)) − 1/ (n+1)-[exp( 1/ n) − 1/ n ]=  h (1 /( n +1))  −h ( 1/ n).  b. En déduire le sens de variation de la suite (un). Pour n >0, la fonction h(n) est strictement croissante. 0 < n < n+1 ; 1/(n+1) < 1 /n. h ( 1/ n) >h (1 /( n +1)) ; un+1 −un < 0, la suite (un) est décroissante.  4. Le tableau ci-dessous donne des valeurs approchées à 10−9 des premiers termes de la suite (un). Donner la plus petite valeur de l’entier naturel n pour laquelle l’écart entre T et Cf semble être inférieur à 10−2 . u8 = 0,0081 < 0,01. Pour x = 1 /8, l'écart entre la courbe et la tangente est inférieur à 0,01.

menu