Synthèse du 2-méthylpropan-2-ol, bac Mayotte 2022.

Le 2-méthylpropan-2-ol est utilisé comme solvant dans les dissolvants pour peintures, dans le carburant pour augmenter l’indice d’octane et comme intermédiaire dans la synthèse d'autres produits chimiques comme les parfums. On se propose d’étudier la synthèse du 2-méthylpropan-2-ol à partir d’un halogénoalcane : le 2- chloro-2-méthylpropane.
Le 2-chloro-2-méthylpropane (noté RCl par la suite) réagit avec l’eau et cette hydrolyse conduit à la formation de 2-méthylpropan-2-ol (noté ROH) et d’acide chlorhydrique modélisée par une réaction dont l'équation est la suivante :
RCl(ℓ) + 2 H₂O(ℓ) --> ROH(ℓ) + H₃O⁺(aq) + Cl^– (aq)
La transformation chimique est supposée totale.
Le protocole expérimental, décrit ci-après, est mis en œuvre.
Dans une fiole jaugée de 100,0 mL, introduire 4,0 mL de 2-chloro-2-méthylpropane et compléter avec de l'acétone jouant le rôle de solvant afin d'obtenir un volume de 100,0 mL d'une solution S.
Dans un bécher, introduire 8,0 mL de solution S à l’aide d’une pipette graduée de 10,0 mL.
Immerger la sonde conductimétrique dans un bécher contenant 32,0 mL d'eau distillée et la relier à une carte d’acquisition.
Verser la solution S dans le bécher contenant l'eau et déclencher en même temps l'acquisition.
Arrêter l'acquisition lorsque la conductivité n'augmente plus.
Suivi temporel de la transformation par conductimétrie.
1. Justifier qu’un suivi temporel de la transformation peut se faire à l’aide de mesures conductimétriques.
Les réactifs ne sont pas sous forme ionique. Deux des produits sont des ions. On peut donc suivre la transformation par conductimétrie.
2. Donner l’expression littérale reliant la conductivité s(𝑡) de la solution et les concentrations en quantité de matière des espèces chimiques concernées.
s(𝑡) =[H₃O⁺] l _H3O+ +[Cl^-] l _Cl-.
À chaque instant, on calcule la concentration en 2-chloro-2-méthylpropane par la relation : [RCl](𝑡) = C₀ × (1 − s(𝑡) / s_finale) . s_finale est la valeur de la conductivité de la solution lorsque la transformation est achevée et C₀ la concentration initiale en RCl.
Cette relation permet de tracer les graphiques donnant l’évolution à 25 °C et à 30 °C de la concentration en RCl en fonction du temps. Ces courbes sont représentéesci-dessous.
3. Déterminer la valeur de la vitesse volumique de disparition du réactif RCl à la date t = 1 min et à 25 °C. Justifier la réponse par un tracé graphique.

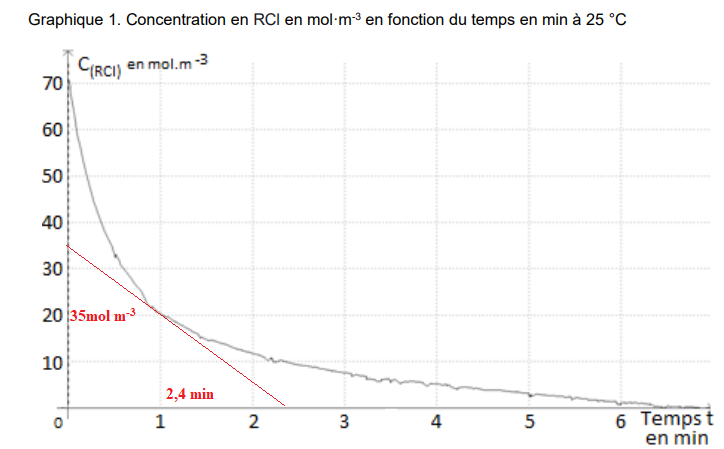
Valeur absolue du coefficient diirecteur de la tangente à la courbe à la date t = 1 min.
35 / 2,4 = 14,6 mol m^-3 min^-1.
4. Déterminer la valeur du temps de demi-réaction à 30 °C, en explicitant la démarche suivie, et la comparer à celle de l’expérience à 25 °C. Proposer une interprétation.

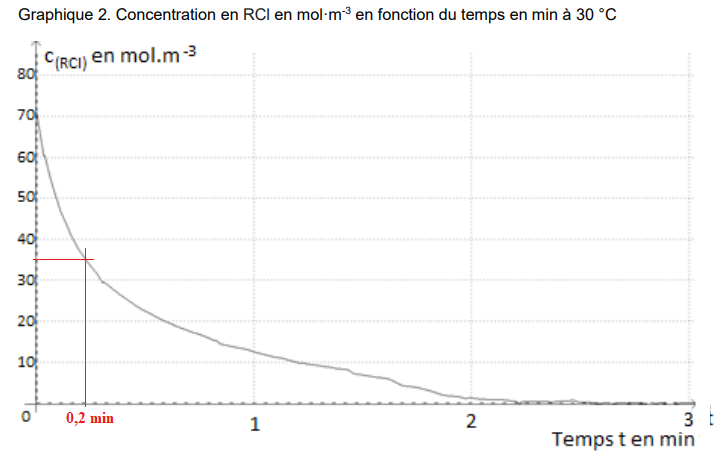
Temps de demi-réaction à 25°C : environ 0,6 min.
Temps de demi-réaction à 30°C : environ 0,2 min.
La température est un facteur cinétique.

B2. Hypothèse sur l’ordre de la réaction par rapport à l’espèce chimique RCl.
Si l’eau est en large excès, la vitesse volumique v de disparition de RCl s'écrit : v = 𝑘 × [RCl](𝑡), où [RCl](𝑡) est la concentration en 2-chloro-2-méthylpropane à la date 𝑡, 𝑘 est la constante de vitesse à la température de l’expérience.
5. 5.1. Donner la définition de la vitesse volumique v de disparition de RCl.
v = - d[RCl](t) / dt.
5.2. Déduire l’expression de l’équation différentielle du premier ordre vérifiée par [RCl](𝑡).
v = 𝑘 × [RCl](𝑡) = - d[RCl](t) / dt.
d[RCl](t) / dt + k [RCl](𝑡) =0.
La solution de cette équation s’écrit [RCl](𝑡) = [RCl]₀ ⋅ exp(−𝑘 ⋅ 𝑡) où [RCl]₀ est la concentration du composé RCl à la date 𝑡 = 0.
5.3. En déduire l’expression du temps de demi-réaction en fonction de la constante de vitesse 𝑘.
[RCl](t½) =½ [RCl]₀₌ [RCl]₀ ⋅ exp(−𝑘 ⋅ 𝑡½)
0,5 = exp(−𝑘 ⋅ 𝑡½)
ln(0,5) = -ln(2)= -k t½ ; t½ = ln(2) / k.
6. On souhaite comparer, à 30 °C, le temps de demi-réaction expérimental déterminé graphiquement à la question 4 et le temps de demi-réaction calculé dans le cadre du modèle de la question précédente.
6.1. La vitesse initiale de disparition de RCl à 30 °C, déterminée sur le graphique 2, étant égale à 3,9 mol·m^-3 ·s^-1 , déterminer la valeur de 𝑘 dans l’hypothèse d’une loi de vitesse d’ordre 1.
v = 𝑘 × [RCl](0) =3,9 ; k = 3,9 / 70 =0,0557 ~0,056 s^-1.
6.2. En déduire la valeur du temps de demi-réaction calculée dans le cadre du modèle de la question 5. Commenter.
t½ = ln(2) / 0,056 =12,4 s ou environ 0,21 min.
Cette valeur est en accord avec la valeur expérimentale. La réaction est donc d'ordre 1.