La stéréophonie se
réfère à un mode de reproduction sonore visant à reconstituer la
répartition dans l'espace des sources d'origine.
On crée la stéréo en utilisant plusieurs canaux audios indépendants
reliés à au moins deux
enceintes, de manière à reconstituer l’espace sonore voulu par
l’artiste. Par exemple, un
signal distribué en quantité égale sur deux enceintes en phase et de
même sensibilité
semblera provenir d’un point virtuel situé entre les enceintes.
Le but de cet exercice est d’étudier l’altération de l’enregistrement
en stéréophonie dans
certaines conditions d’écoute.
Données :
− intensité sonore au seuil d’audibilité à 1 kHz : 𝐼
0 = 1,00 × 10
−12 W
∙ m
2
;
− célérité du son dans l’air dans les conditions de l’exercice : 𝑣
= 340 m ∙ s
−1
.
On considère deux enceintes acoustiques identiques dans un espace
libre, c’est-à-dire sans
parois pouvant créer une réverbération par réflexion. Chaque enceinte
acoustique est
modélisée par une source sonore ponctuelle (S
1 et S
2) pouvant émettre
dans toutes les
directions tout le spectre audible entre 20 Hz et 20 000 Hz avec une
intensité sonore
constante.
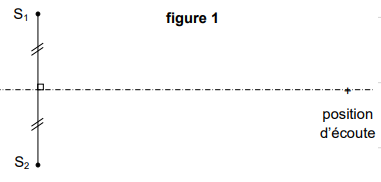
La position d’écoute est située sur la médiatrice du segment formé par les deux sources S
1
et S
2 . Lorsque seule la source 1 est branchée, le niveau
d’intensité sonore à la position d’écoute est 𝐿
1.
1. S
2 délivre le même signal sonore que S
1. En l’absence d’interférences entre les deux
sources, déterminer l’expression 𝐿
1+2 du niveau d’intensité sonore en fonction de 𝐿
1.
I
1 =I
2 = I
0 10
0,1 L1 ; I
total = 2 I
1.
L
1+2 = 10 log (2I
1 / I
0) =10 log
(I1 / I0) + 10 log 2 = L1 +3 dB.
2. On s’intéresse maintenant au phénomène d’interférences entre les ondes issues des
deux sources supposées identiques et émettant des signaux de même fréquence et
en phase. Préciser s’il y a interférences constructives ou destructives dans cette
position d’écoute. Justifier.
La différence de marche entre les ondes étant nulle et les signaux
étant en phase, les interférences son constructives à la position
d'écoute.
3. Donner la condition nécessaire pour que la position d’écoute soit un lieu
d’interférences destructives.
La différence de marche entre les deux signaux doit être un multiple impair de la demi-longueur d'onde à la position d'écoute.
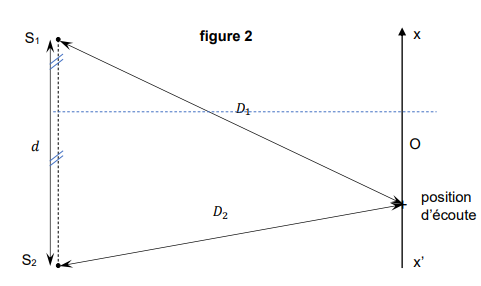
La position d’écoute est maintenant telle que 𝐷
1 = 3,34 m, 𝐷
2 = 3,00 m et 𝑑 = 2,00 m
comme indiquée sur la figure ci-dessous.
 4.
4. Exprimer et calculer la longueur d’onde 𝜆
1 la plus grande pour laquelle les
interférences sont destructives.
Différence de marche :
d = D
1-D
2 = 3,34 -3,00 = 0,34 m.
l1 = (
D1-D2) / (2k+1) avec k = 0.
l1 =0,34 m.
5. Déterminer les quatre premières fréquences pour lesquelles le niveau d’intensité
sonore perçu est diminué par le phénomène d’interférence. On introduira au besoin un
entier 𝑘.
Le niveau d’intensité
sonore perçu est diminué par les’interférences destructives.
l1 = (D1-D2) / (2k+1) = v / f.
f = (2k+1) v / (D1-D2).
k =0 ; f 0=340 / 0,34 = 1,00 kHz.
k =1 ; f 1=3 * 340 / 0,34 = 3,00 kHz.
k =2 ; f 2=5 * 340 / 0,34 = 5,00 kHz.
k =3 ; f 3= 7 * 340 / 0,34 = 7,00 kHz.
6. Un auditeur se déplace sur l’axe (x’x) représenté sur la figure 2 de la position d’écoute
précédente vers le point O. Décrire qualitativement comment évoluent les fréquences
perturbées par le phénomène d’interférence. Justifier.
La différence de marche diminue jusqu'à s'annuler.
Les longueurs d'onde précédentes diminuent et les fréquences correspondantes augmentent.
7. Expliquer avec des considérations physiques issues des questions précédentes en
quoi l’écoute d’une séquence audio en stéréophonie peut être altérée.
La séquence n'est pas altérée si l'auditeur se place à l'un des sommets
d'un triangle équilatéral, les deux enceintes étant situées aux deux
autres sommets.