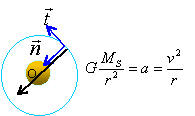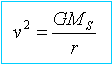D’après
la troisième loi de Kepler, la période de révolution d’une planète
autour du Soleil dépend uniquement de la valeur du demi-grand axe de sa
trajectoire elliptique. Dans le cas des planètes du Système solaire, on
constate ainsi que, plus elles sont proches du Soleil, plus la période
de révolution est faible. Pourtant, certains objets semblent ne pas
vérifier la
troisième loi de Kepler.
Le satellite SOHO est chargé d’observer en continu le Soleil afin d’en
étudier la structure interne, les processus produisant le vent solaire
ainsi que la couronne solaire. Le satellite est placé sur une orbite
circulaire centrée sur le Soleil ; le Soleil, le satellite et la Terre
sont alignés à tout instant. La position du satellite sur l’axe
Terre-Soleil est constante au cours
du temps et se situe à une distance de la Terre d’environ 1,496 ×10
6
km. L’orbite de la Terre autour du Soleil est considérée comme
circulaire.
Données :
• constante de gravitation universelle : G = 6,674×10
-11 m
3∙kg
-1∙s
-2 ;
• masse du Soleil : M
S = 1,989×10
30 kg ;
• masse de la Terre : M
T = 5,974×10
24 kg ;
• distance moyenne Soleil-Terre : R
T = 1,496×10
8 km ;
• distance entre le Terre et le satellite SOHO : d = 0,015×10
8 km ;
• rayon de l’orbite de SOHO autour du Soleil : r = 1,481×10
8 km ;
• période de révolution terrestre : T
T = 365,2 jours.
L’étude est conduite dans le reférentiel héliocentrique dont l’origine
est confondue avec le centre du Soleil et dont les axes pointent vers
des étoiles lointaines. Il est supposé galiléen.
Q1. Justifier, à l’aide d’une analyse conduite dans le repère de Frenet, que le mouvement du satellite SOHO est uniforme.
La seule force appliquée est la force gravitationnelle exercée
par le soleil.
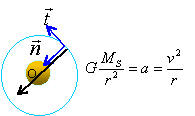
Le vecteur accélération est dirigé vers le centre du soleil.
La composante de l'accélération étant nulle suivant le vecteur
t de la base de Frenet, la norme du vecteur vitesse ne change pas
(mouvement uniforme)
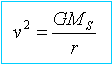
Q2. À l’aide d’un
argument géométrique, montrer que la période de révolution du satellite
SOHO autour du Soleil est la même que celle de la Terre autour du
Soleil.
Le satellite est placé sur une orbite
circulaire centrée sur le Soleil ; le Soleil, le satellite et la Terre
sont alignés à tout instant. La position du satellite sur l’axe
Terre-Soleil est constante au cours du temps
Q3. Énoncer la
troisième loi de Kepler, l’exprimer dans le cas de la Terre. Montrer
alors, à l’aide de la question 2, que la troisième loi de Kepler n’est
pas vérifiée dans le cas de l’étude du mouvement du satellite SOHO
autour du Soleil.
Le carré de la période de révolution est proportionnelle au cube du rayon de l'orbite.
T
T2 / R
T3 = 4
p2 / (GM
S).
Pour le satellite Soho :
TT2 / r3 diffère de 4 p2 / (GMS).
La période de SoHO est égale à la période de révolution de la Terre autour du Soleil soit environ 365 jours.
La période de révolution
T' d'un satellite soumis à la seule force gravitationnelle exercée par
le Soleil ne dépend que du rayon r de l'orbite ( T² = K . r3 ).
Le rayon de la
trajectoire de SoHO devrait être égal à celui de l'orbite de la Terre ;
ce n'est pas le cas, donc il y a au moins une autre force à considérer.
On cherche désormais à comprendre pourquoi, dans le cas de l’étude du
mouvement du satellite SOHO, la troisième loi de Kepler n’est pas
vérifiée.
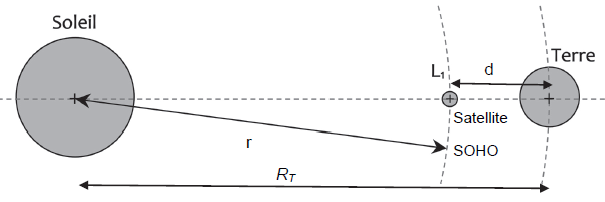
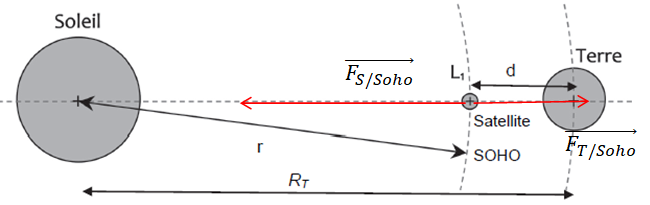
Q4. Reproduire sur
la copie le schéma de la figure 1 ci-dessus et y représenter
qualitativement les forces gravitationnelles exercées respectivement
par le Soleil sur le satellite et la Terre sur le satellite. Ce tracé
se fera sans souci d’échelle.
 Q5.
Q5. Compte tenu de
la trajectoire du satellite, déterminer laquelle des deux forces est la
plus intense. Justifier précisément la réponse.
Q6. Déterminer la valeur du rapport FS/Soho / FT/Soho .Commenter.
F
S/Soho = GM
S m / r
2 ;
FT/Soho = GMT m / d2 ;
r ~ 100 d ; MS ~ 3 105 MT :
FS/Soho ~ G *3 105 MT / (100d)2 ~30 GMT m / d2 ~30 FT/Soho .
Q7. Proposer une
explication qualitative au fait que la troisième loi de Kepler soit
valable dans le cas de l’étude du mouvement des planètes du Système
solaire, mais pas dans le cas de l’étude du mouvement du satellite SOHO
autour du Soleil.
Les planètes du système solaire sont suffisamment éloignées les unes
des autres. L'action d une planète sur une autre est négligeable devant
l'action du soleil sur cette même planète, ainsi seule l'action du
soleil peut être prise en compte.
L'action exercée par la terre su Soho n'est pas négligeable devant
l'action exercée par le soleil sur Soho. La troisième loi de Kepler
n'est pas appliquable dans le cas de Soho.
Q8. Justifier de l’interêt de placer le satellite SOHO à cet endroit particulier du système Terre-Soleil.
Soit un objet orbitant autour du Soleil, plus près de celui-ci que la Terreet situé sur une même ligne. Cet objet subit l'attraction solaire supérieure à celle de la Terre ; il tourne donc plus rapidement autour du Soleil que la Terre.
Mais la gravité terrestre contrecarre en partie la gravité du Soleil : ce qui ralentit cet objet.
Plus l'objet est proche de la Terre, plus cet effet est important.
À un certain point, le point L1 ( point de Lagrange ), l'objet et la Terre ont la même vitesse angulaire.
Soho est donc immobile par rapport à la terre et au soleil.
SOHO peut ainsi observer en continu le Soleil.