Les douanes s’intéressent aux importations de casques audio portant le logo d’une certaine
marque. Les saisies des douanes permettent d’estimer que :
- 20 % des casques audio portant le logo de cette marque sont des contrefaçons ; -
2 % des casques non contrefaits présentent un défaut de conception ;
- 10 % des casques contrefaits présentent un défaut de conception.
L’agence des fraudes commande au hasard sur un site internet un casque affichant le logo
de la marque. On considère les évènements suivants :
- C : « le casque est contrefait »;
- D : « le casque présente un défaut de conception ».
Dans l’ensemble de l’exercice, les probabilités seront arrondies à 10
−3
si nécessaire.
Partie 1
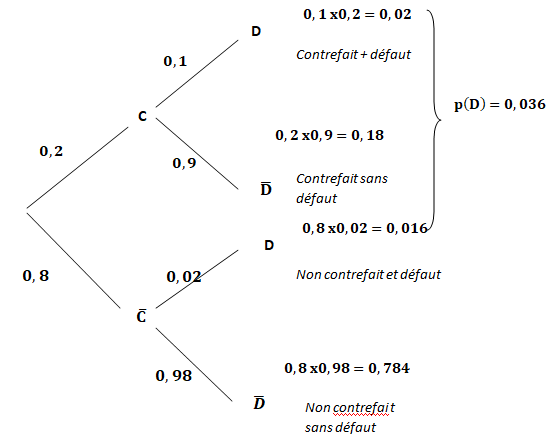 1.
1. Calculer P(C ∩D). On pourra s’appuyer sur un arbre pondéré.
2. Démontrer que P(D) = 0,036.
3. Le casque a un défaut. Quelle est la probabilité qu’il soit contrefait ?
P(C n D) / P(D) = 0,02 / 0,036 =0,556.
Partie 2.
On commande n casques portant le logo de cette marque. On assimile cette expérience à un
tirage aléatoire avec remise. On note X la variable aléatoire qui donne le nombre de casques
présentant un défaut de conception dans ce lot.
1. Dans cette question, n = 35.
a. Justifier que X suit une loi binomiale B(n, p) où n = 35 et p = 0,036.
On répète 35 fois une épreuve de Bernoulli, de façon indépendante.
Probabilité du succès ( casque avec défaut) est p = 0,036.
b. Calculer la probabilité qu’il y ait parmi les casques commandés, exactement un
casque présentant un défaut de conception.
P(X=1)=(
35 1)x0,036
1x(1-0,036)
34=0,362.
c. Calculer P(X
< 1).
P(X < 1).= P(X=0) + P(X=1)=0,277 +0,362=0,639.
2. Dans cette question, n n’est pas fixé.
Quel doit être le nombre minimal de casques à commander pour que la probabilité
qu’au moins un casque présente un défaut soit supérieur à 0,99 ?
P(X
>1) =1-P(X=0) =1-(
n0) x0,036
0 x0,964
n = 1-
> 0,99.
0,01
>0,964n .
ln(0,01) > n ln(0,964).
-4,605 > -0,0367 n.
n > 126.