La physique du son sur un téléphone portable, bac Métropole 2022

L’application phyphox dispose de modules acoustiques très utiles pour mener des expériences sur les ondes à l’aide d’un téléphone portable. Le module Générateur de son permet de produire une onde sonore sinusoïdale à une fréquence déterminée, tandis que le module Intensité sonore permet de déterminer l’intensité sonore d’un son. Il s’agit dans cet exercice d’étudier des phénomènes ondulatoires à l’aide de téléphones portables munis de l’application phyphox .
Donnée : − directivité : le microphone et le haut-parleur d’un mobile multifonction sont directifs, c’est-àdire qu’ils sont d’autant plus efficaces que la direction de propagation de l’onde reçue ou émise est perpendiculaire au microphone ou au haut-parleur.

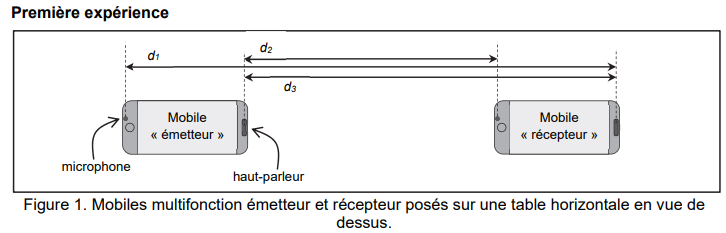
Le mobile multifonction « émetteur » produit une onde sonore sinusoïdale de fréquence f = 2,00×10³ Hz.
Q1. L’intensité sonore mesurée par le mobile « récepteur » vaut I₁ = 2,0×10^–7 W·m^-2. Calculer la valeur du niveau d’intensité sonore L₁ correspondant.
L₁ = 10 log(I₁ / I₀) = 10 log(2,0 10^-7 /10^-12) =53 dB.
Dans le modèle d’atténuation géométrique de l’intensité sonore, on considère le cas d’une source sonore qui émet de la même manière dans toutes les directions. On montre alors que l’intensité sonore varie proportionnellement à l’inverse du carré de la distance à la source.
Q2. Dans le cadre du modèle d’atténuation géométrique et au moyen d’une approche énergétique, expliquer qualitativement à l’aide d’un schéma l’emploi du terme « géométrique » pour rendre compte de la baisse de l’intensité sonore lorsque la distance à la source augmente.
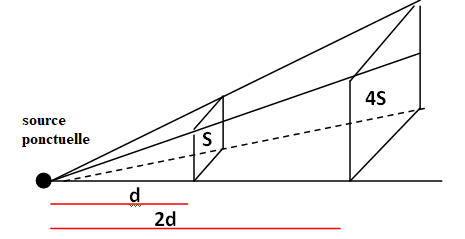
L'énergie E₀ de la source est répartie de la même manière dans toutes les directions.
A la distance d, une partie de cette énergie traverse la surface S.
A la distance 2d, cette même énergie est répartie sur une surface 4 fois plus grande. l'onde sonore paraît moins forte. Elle s'atténue pour des raisons géométriques.

Q3. Identifier parmi les expressions suivantes celle qui exprime d’, distance pour laquelle l’intensité sonore vaut la moitié de celle mesurée à la distance d. Justifier.
a. d’ = d / 2^½ ; b. d’ = 2×d c. d’ =2^½d . d. d’ = d /2 e. d’ = 4×d.
I = Cste / d² ; I' = 0,5 I = Cste / d'².
0,5 / d² = 1 / d '² ; 0,5 d'² =d² ; d'² = 2 d² ; d' = 2^½d.
Q4. Des mesures, non présentées ici, effectuées dans les conditions décrites dans la question Q3 sont en contradiction avec le modèle présenté en introduction de la question Q2. Proposer au moins une hypothèse expliquant l’écart entre les prévisions du modèle et les mesures.
Le son du haut-parleur n'est pas émis de la même manière dans toutes les directions.
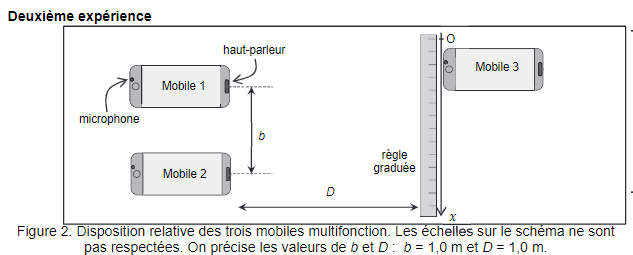
Deux mobiles multifonction sont disposés côte à côte (numérotés 1 et 2) comme l’indique la figure suivante. Chacun d’eux dispose du module « Générateur de son » de phyphox. Les modules sont activés afin de produire un son sinusoïdal de fréquence f = 2,00×10³ Hz.

Q5. Déterminer la valeur de la longueur d’onde des ondes émises.
l = c / f = 340 / 2000 =0,17 m.
Q6. Identifier et nommer le phénomène physique en jeu lorsque les mobiles multifonction 1 et 2 émettent simultanément des ondes sonores sinusoïdales de même fréquence. Justifier à l’aide d’un schéma reprenant les éléments de la figure.
Interférences sonores.
En certains points les interférences sont constructives, le son est plus fort.
En d'autres points les interférences sont destructives, le son est moins fort.
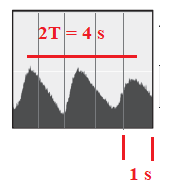
L’expérimentateur déplace le mobile multifonction 3 le long de la règle graduée (suivant l’axe Ox) à une vitesse constante d’environ v = 0,10 m·s^–1, pendant que le son est enregistré à l’aide du dictaphone. On constate que l’amplitude du son varie périodiquement comme l’indique la figure suivante.

Q7. L’interfrange i est définie comme la distance entre deux maxima le long de l’axe Ox. Estimer la valeur de l’interfrange à partir de la figure .
Distance parcourue en 2 secondes : i = v t = 0,1 x2 = 0,2 m = 20 cm.
L’interfrange i est liée à la distance b entre les deux sources, à la distance D entre les deux sources et le récepteur et à la longueur d’onde l du signal selon la relation :
i = l × D / b[1 +b² / (4D²)]^½.
Q8. Établir le sens d’évolution de l’interfrange i lorsque la fréquence augmente et que les autres paramètres restant constants. En déduire l’évolution de la période temporelle de l’enregistrement de la figure du mobile multifonction 3, pour la même vitesse de déplacement du mobile multifonction.
Si la fréquence augmente, la longueur d'onde diminue. l'interfrange i diminue.
Les pics seront plus proches et la période temporelle sera plus courte.
Q9. Calculer la valeur de l’interfrange à l’aide de la relation donnée ci-dessus et la comparer avec celle déterminée graphiquement à la question Q7. Conclure.
i = 0,17x 1,0 / 1 x[1+1² / (4 x1²)]^½ = 0,17 x1,25^½ =0,19 m.
En accord avec la valeur trouvée à la question Q7 ( écart relatif 5 %).