Les panneaux photovoltaïques sont
recouverts d’une plaque de verre trempé pour résister
aux impacts tels que ceux provoqués par la grêle.
Pour répondre aux normes fixées par la Commission Électrotechnique Internationale, les
panneaux photovoltaïques sont soumis, selon la norme internationale CEI 61215 pour
modules photovoltaïques au silicium cristallin, à des tests durant lesquels ils sont
bombardés par des billes de glace de 25 mm de diamètre, de masse 7,53 g et de vitesse
83 km·h
-1.
La grêle se forme dans les cumulonimbus situés entre 1 000 m et 10 000 m d’altitude où la
température peut descendre en dessous de 0 °C. Un grêlon tombe lorsqu’il n’est plus
maintenu par les mouvements de l’air au sein du nuage. Certains d’entre eux peuvent
atteindre des vitesses avoisinant 100 km·h
-1 lorsqu’ils arrivent au sol.
On étudie la chute d’un grêlon de masse m = 7,53 g qui tombe d’un point O d’altitude
h = 1 500 m sans vitesse initiale. Le point O sera pris comme origine d’un axe (Oz) orienté
positivement vers le bas. La masse du grêlon est supposée constante au cours de la
chute.
Partie A - Chute libre
1. En appliquant la deuxième loi de Newton, déterminer les coordonnées cartésiennes
des vecteurs accélération, vitesse et position du centre de masse G du grêlon, si l’on
considère qu’il tombe en chute libre.
Le gêlon n'est soumis qu'à son poids.
La seconde loi de Newton écrite sur l'axe vertical orienté vers le bas donne : a = g.
La vitesse est une primitive de l'accélération et la vitesse initiale est nulle.
v = g t
La position est une primitive de la vitesse et la position initiale est z = h.
z = ½gt
2 +h.
2. Calculer, en expliquant la démarche, la valeur de la vitesse du grêlon lorsqu’il atteint le
sol. Indiquer si le résultat obtenu est vraisemblable et discuter les hypothèses du
modèle retenu.
Variation de l'énergie cinétique = travail moteur du poids en descente.
½mv2 -0 = mgh ; v
2 = 2gh =2 x9,8 x1500 =2,94 10
4.
v =1,7 10
2 m /s ou 1,7 10
2 x3,6 =180 km / h.
Cette valeur est trop grande ; le grêlon n'est pas en chute libre.
Partie B - Vitesse limite.
Données : masse volumique de l’air à 0 °C :
rair = 1,29 kg·m
-3 ; coefficient de frottement de l’air : k = 1,40 × 10
-4 kg·m
-1.
En réalité, le grêlon de masse m = 7,53 g, assimilé à une sphère de rayon R = 12,5 mm,
est soumis à deux autres forces, la force de frottement de l’air, opposée au vecteur vitesse
du grêlon, et la poussée d’Archimède.
On modélise la valeur f de la force de frottement exercée par l’air sur le grêlon par
l’expression : f = k × v
2, où K sera appelé coefficient de frottement de l’air et v la
vitesse du centre de masse du grêlon.
La poussée d’Archimède exercée par l’air sur le
grêlon est une force verticale, orientée vers le haut, dont la valeur a pour expression : F
A =
rair V g où V est le volume du grêlon.
À cause des frottements de l’air, la vitesse du grêlon cesse d’augmenter après quelques
secondes et devient constante. On dit que le grêlon atteint sa vitesse limite.
3. Calculer la valeur de la poussée d’Archimède exercée par l’air sur le grêlon et la
comparer à la valeur du poids du grêlon. Conclure.
Volume du grêlon : V = 4 /3
p R
3 = 4 / 3 x3,14 x(12,5 10
-3)
3 =8,2 10
-6 m
3.
FA = rair V g =1,29 x8,2 10-6 x9,8=1,0 10-4 N.
Poids = mg = 7,53 10-3 x9,8 =7,4 10-2 N >> poussée d'Archimède.
4. En tenant compte de la conclusion précédente, déterminer par le calcul la valeur de la
vitesse limite du centre de masse du grêlon. Vérifier si ce résultat est cohérent avec la
vitesse des billes de glace utilisées pour tester la résistance des panneaux.
La vitesse limite étant atteinte, la force de frottement compense le poids.
mg = k v
lim2 ;
vlim2 =7,4 10-2 / (1,40 10-4) =527 ; vlim =23 m /s ou 23 x3,6 =83 km / h.
Il s'agit de la vitesse à laquelle sont éffectués les tests.
5. Les évolutions temporelles de la vitesse et de la position du centre de masse G du
grêlon étant données.
Déterminer à quelle hauteur se trouve le grêlon
lorsque sa vitesse atteint 95 % de sa vitesse limite.
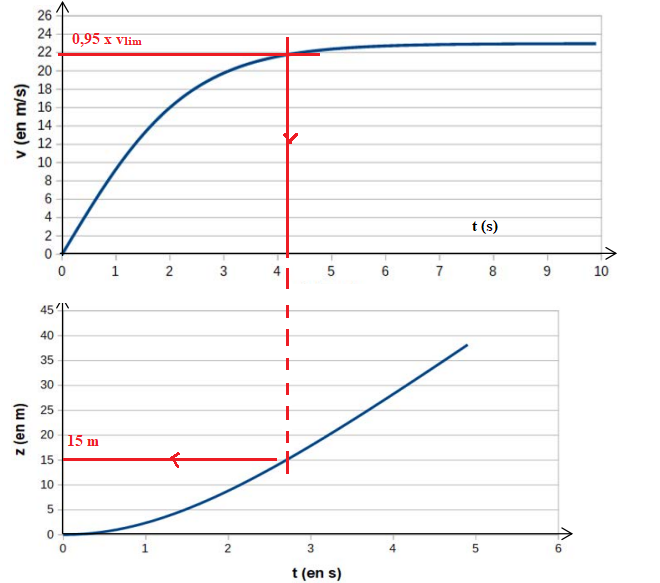
Le grêlon aparcouru 15 m et se trouve à l'altitude de 1500-15 =1485 m.