L'airbag,
dipole RC, étude d'un crash-test, charge explosive, bac G
Amérique du Sud 2022.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
L’AIRBAG
Un airbag, ou coussin gonflable de sécurité, est une
membrane ou enveloppe flexible dans laquelle un gaz est très rapidement
injecté par une transformation chimique explosive pour gonfler
l'enveloppe et ainsi amortir un choc.
Les airbags sont principalement utilisés dans les automobiles pour
protéger les passagers lors d'une collision et ainsi leur éviter une
décélération excessive en percutant certains accessoires de la voiture.
Partie 1. Étude d’un
circuit RC et application à un détecteur de choc
Les airbags sont déclenchés par une chaîne électronique utilisant un
capteur d’accélération, tel que l’accéléromètre MEMS (Micro-Electro-Mechanical-System).
Le but de cette partie est de montrer qu’un MEMS se comporte comme un
circuit RC.
1. On s’intéresse à la réponse d’un circuit RC soumis à un signal
d’entrée uG(t) ayant la forme d’une tension en créneaux.
Cette tension en créneaux prend alternativement des valeurs E et 0 V,
sa période est notée T.
1.1. À l’aide de la figure, déterminer la valeur de E ainsi que
celle de la fréquence f de la tension en créneau uG(t).
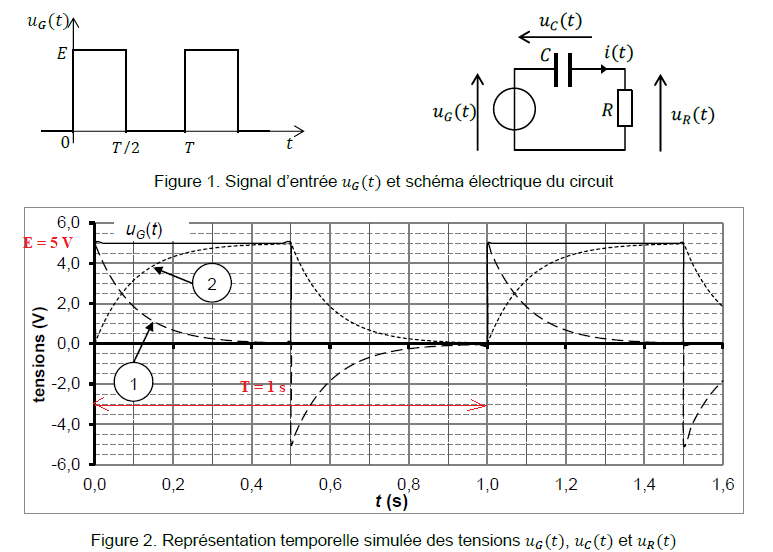
E = 5 V ; T = 1 s ; f = 1/ T =1 Hz.
1.2. Établir l’expression de l’intensité i(t) du courant circulant dans
le circuit en fonction de et duC(t)/dt.
Q(t) =C UC(t) ; i(t) = dq(t) / dt = C duC(t)/dt.
1.3. À t=0 s, la tension uG(t) passe de 0 V à 𝐸. Le condensateur
est initialement déchargé. On étudie dans cette question la phase de
charge du condensateur entre t=0 s et t=0,5 T.
1.3.1. Établir l’équation différentielle vérifiée par la tension uC(t) aux bornes du condensateur lorsque uG(t)=E.
Additivité des tensions : E = uR(t) + uC(t) = R i(t) +uC(t) =RCduC(t)/dt + uC(t).
1.3.2. Vérifier que uC(t)=E(1−exp(−t /(RC)) est solution de
l’équation différentielle.
duC(t)/dt =E / (RC) exp(−t /(RC)).
Repport dans l'équation différentielle :
RC E / (RC) exp(−t /(RC)) + E(1−exp(−t /(RC)) = E est vérifié quel que soit t.
1.3.3. À partir de l’expression de uC(t), montrer que uR(t)=E exp(−t /(RC)).
i(t) = C duC(t)/dt = E / R exp(−t /(RC)).
uR(t)=Ri(t) = E exp(−t /(RC)).
1.4. Associer les courbes 1 et 2 de la figure aux tensions uC(t)
et uR(t). Justifier.
Durant la charge du condensateur :
uR(0) = E et uR(t) tend vers zéro si t est assez grand : courbe 1.
uC(0)=0 et uC(t)= tend vers E si t est assez grand : courbe 2.
1.5. Les représentations temporelles de ces tensions ont été simulées
avec C=1 μF. Estimer la valeur de la résistance en explicitant la
méthode.
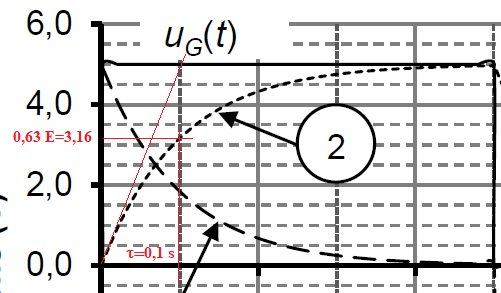
t=RC = 0,1 s ; R = 0,1 / 10-6 = 105 ohms.
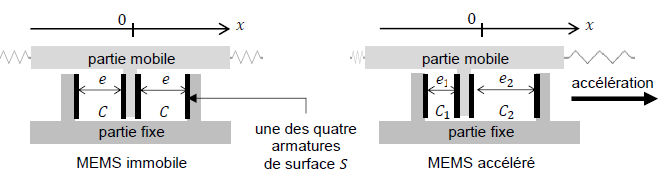
2. L'accéléromètre MEMS est constitué d'une partie mobile qui, soumise
à une accélération, entraîne le déplacement de l’armature commune aux
deux condensateurs. En l’absence d’accélération, chaque condensateur a
une capacité C. On considère un déplacement de l’accéléromètre MEMS
suivant Ox, lorsqu‘il est soumis à une accélération, leurs capacités
prennent respectivement les valeurs C1 et C2 comme l’illustrent les
schémas de la figure.
2.1. La capacité d’un condensateur plan dont les armatures ont une
surface S et sont séparées d’une distance e est donnée par la
relation :
C=eS / e où e est une constante.
Comparer C1 et C2 en justifiant la réponse.
e et S étant constants : C1 croît car e 1 < e ; C2 décroît car e 2 > e.
On suppose que les capacités sont reliées à l’accélération par les
relations suivantes :
C1= C(1+k⋅ax) et C2= C(1-k⋅ax) où k est une constante positive et ax est la composante de l’accélération suivant l’axe Ox.
2.2. Donner le signe de ax qui permet de rendre compte de la
situation schématisée sur la figure. Commenter.
C1 > C, k >0, donc ax est positif en cas d'accélération.
Un circuit électrique non décrit permet de délivrer une tension de
sortie continue Vout reliée à la composante de l’accélération ax
par la fonction affine : Vout=V0+S ax où V0 est une tension
continue et S est appelée sensibilité du capteur d’accélération.
2.3. Pour un accéléromètre dédié à la détection d’un accident frontal
et au déclenchement d’un airbag, S=27 mV / g avec g=9,8 m⋅s-2. Donner
la signification physique de V0 et calculer la variation de la valeur
de la tension de sortie pour une accélération suivant Ox de 40 g.
Commenter.
V0 est la tension correspondant à un mouvement rectiligne uniforme.
Vout-V0=S ax =0,027 x40 =1,08 V.
|
...
|
....
|
Partie 2. Étude d’un crash-test
Un essai de choc (crash-test) est une opération réalisée en laboratoire
consistant à tester le comportement des véhicules en cas de choc ou de
collision. Le véhicule testé est projeté à une vitesse donnée sur un
obstacle massif de façon à reconstituer les conditions d'un choc et de
mesurer les déformations du véhicule et les dommages causés aux
passagers. Ceux-ci sont remplacés par des mannequins.
La figure 4 présente trois images issues de la vidéo d’un crash-test.
Le chronométrage est indiqué en millisecondes en haut à gauche sur
chaque photo.
L’impact a lieu à la date 𝑡=0 s. Toutes les photos sont à la même
échelle.

1. Lors du crash-test, la voiture arrive à vitesse donnée sur
l’obstacle.
À partir des images, évaluer cette vitesse en km⋅h–1. Détailler la
démarche.
40 cm sont parcourus en 24 ms ; v = 0,40 / 0,024 ~17 m/ sou 17 x3,6 ~60 km / h.
2. L’analyse de la vidéo permet de représenter les vitesses d’une des
mires de la portière arrière de la voiture et de la tête du mannequin
simulant le conducteur.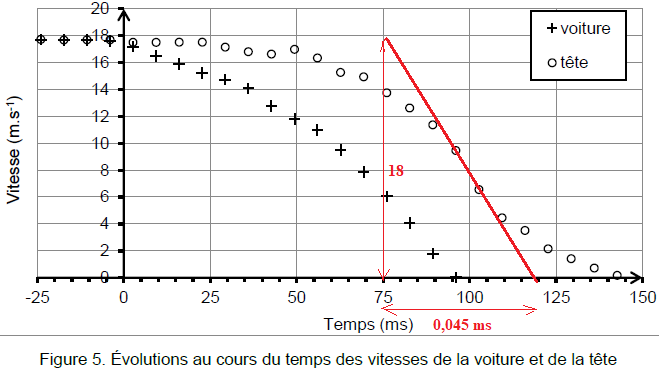
2.1. Caractériser le mouvement de la tête pendant les 25 ms suivant la
date de l’impact qui a lieu à la date t=0 s.
La vitesse de la tête étant constante, son mouvement est rectiligne uniforme.
2.2. Schématiser sommairement la voiture à la date t=75 ms et
représenter sans souci d’échelle ses vecteurs vitesse et accélération.
La vitesse diminue, le vecteur accélération a le sens contraire du vecteur vitesse.
2.3. Estimer la valeur maximale de l’accélération subie par la tête du
mannequin au cours du choc. Détailler la démarche.
Pente de la tangente à la courbe à t = 100 ms, date de la variation maximale de la vitesse de la tête.
Valeur de l'accélération : 18 / 0,045 = 400 m s-2 ou 400 / 9 ,81~ 41 g.
La courbe suivante délimite la zone de forte probabilité d'apparition
d'une commotion cérébrale en fonction de la valeur et de la durée de
l’accélération subie par la tête.
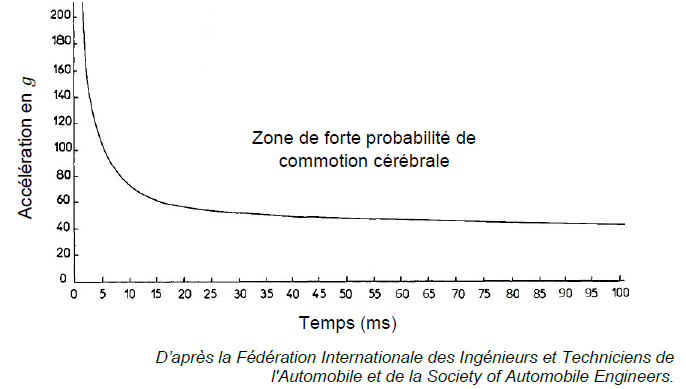
2.4. La probabilité d’apparition d’une commotion cérébrale est-elle
importante pour un conducteur lors d’un choc similaire à celui réalisé
lors du crash-test étudié ? Justifier.
Non, l'accélération n'est que de 41 g. Quel que soit le temps, cette
valeur est en dehors de la zone de forte probabilité de commotion
cérébrale.
Partie 3. Charge explosive.
Données :
Espèce chimique
NaN3 : M =65 g / mol ;
KNO3 : M = 101,1 g / mol.
Pression atmosphérique : P0=101 kPa ;
Constante des gaz parfaits : R=8,31 J·mol–1·K–1 ;
Lorsqu’une accélération excessive est détectée, un mélange constitué
d’azoture de sodium (NaN3) et de nitrate de potassium (KNO3) contenu
dans une cartouche est mis à feu.
Cette mise à feu produit du diazote, gaz nécessaire au gonflage de
l’airbag. La modélisation de cette transformation chimique, supposée
totale, conduit à la réaction dont l’équation est la suivante :
10 NaN3(s) + 2 KNO3(s) → 16 N2(g) + K2O(s) + 5 Na2O(s)
1. Rappeler l’équation d’état du gaz parfait en précisant les unités de
chacune des grandeurs.
PV = n RT.
P : pression en pascal ; V : volume en m3 ; n : quantité de matière (mol) ; T température en K.
2. Dans le cadre du modèle du gaz parfait, déterminer la valeur de la
quantité de matière de diazote permettant, à 20 °C et à la pression
atmosphérique, le gonflement d’un airbag de 60 L, volume moyen d’un
airbag conducteur.
n = PV / (RT) =1,01 105 x0,060 /(8,31 x293)=2,489 ~2,5 mol
3. Montrer que la masse minimale d’azoture de sodium nécessaire à la
production de diazote pour le gonflement de l’airbag est de 101 g. En
déduire la masse minimale de nitrate de potassium que doit contenir la
cartouche.
n(
NaN3) =10 / 16 x2,5 ~mol.
Masse = 1,56 x 65 ~101 g.
n(
KNO3) =2 / 16 x2,5 =0,31 mol soit 0,31 x 101,1 ~31,6 g.
4. Le volume occupé par les réactifs solides est égal à 70 cm3.
Expliquer l’intérêt d’utiliser un dispositif avec des réactifs solides
plutôt que du diazote stocké dans un réservoir sous pression à la
température de 20 °C.
Ordre de grandeur de la pression à laquelle il faudrait comprimer, dans un réservoir de 500 mL, la quantité de diazote nécessaire au gonflement du sac de 60 L sous 1 bar à 293 K :
P= nRT/V avec n=2,5 mol; T=293 K et V= 5 10-4 m3 ;
P= 2,5*8,31*293 / 5 10-4 = 1,2 107 Pa = 120 bars.
Intérêt d'utiliser un dispositif chimique plutôt qu'un dispositif de libération d'un gaz sous pression :
Le volume de stockage "chimique" est 7 fois plus petit que le volume de stockage d'un gaz comprimé.
|
|