Observation de la Lune depuis la Terre, bac G Amérique du Sud 2022. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... Lorsqu’on observe la face visible de la Lune, on distingue de grandes étendues sombres, appelées mers lunaires, et des milliers de petites tâches correspondant à des cratères. On peut en voir plusieurs dizaines de milliers depuis la Terre, mais il en existe en réalité plusieurs millions. 1. La face cachée de la Lune L’objectif de la première partie est de comprendre l’expression « face cachée de la Lune ». Données : − on se place dans le référentiel géocentrique. Son origine correspond au centre de la Terre et ses axes pointent en direction d’étoiles lointaines. Il est supposé galiléen ; − constante de gravitation universelle : 𝐺 = 6,67 × 10−11 m3∙kg-1∙s-2 ; − distance moyenne Terre-Lune : dTL = 3,844 × 105 km ; − masse de la Terre : MT = 5,97 × 1024 kg ; − expression de la norme du vecteur vitesse du centre de la Lune sur son orbite : vL = [GMT / dTL]½. − période de rotation de la Lune sur elle-même : PL = 27,3 jours. 1.1. Établir l’expression de la période de révolution TL de la Lune autour de la Terre, puis calculer sa valeur. La Lune décrit la circonférence 2 p dTL à la vitesse vL pendant la durée TL. 2 p dTL =vLTL = [GMT / dTL]½ TL. TL =2 p dTL1,5 /  [GMT ]½ =2 x3,14 x(3,844 × 108)1,5 / [6,67 × 10−11 x 5,97 × 1024]½ =4,73 1013 / (2 107) ~2,37 106 s ou 27,3 jours. 1.2. Comparer la valeur de TL à la période de rotation de la Lune sur elle-même PL. TL = PL. 1.3. Sur le schéma donné, ajouter la position de la Lune et du point P aux dates PL /4, PL /2 et 3PL /4 . En déduire, dans le cadre de ce modèle simple, pourquoi on parle de « face cachée de la Lune ». 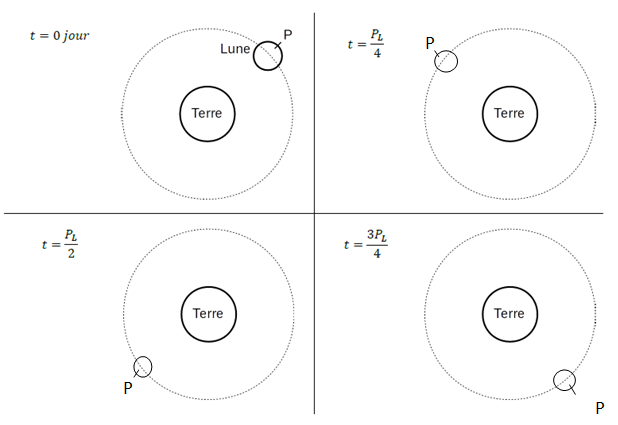Le point P reste toujours invisible depuis la Terre. Le cratère Tycho, situé dans l'hémisphère sud de la face visible de la Lune, est né il y a un peu plus d'une centaine de millions d'années suite à l'impact d'un astéroïde. Son diamètre est de 86 km. Le centre du cratère est occupé par un ensemble de montagnes dont la base s’étale sur une quinzaine de kilomètres. Le piton central s'élève à plus de 2 000 mètres d’altitude. L’objectif de cette deuxième partie est de concevoir une lunette astronomique permettant de visualiser certains détails de la surface lunaire depuis la Terre. 2. Observation de la Lune depuis la Terre. Données : − le pouvoir séparateur de l’oeil humain est la valeur minimale de l’angle q, supposé petit devant 1 rad, sous lequel l’oeil peut distinguer deux points lumineux A et B : e = 2,9 × 10−4 rad. 2.1. Calculer l’angle q sous lequel est vu le cratère Tycho depuis la Terre. En déduire s’il est possible de distinguer les contours du cratère à l’oeil nu. q ~diamètre du cratère / distance Terre Lune =86 / (3,844 × 105 ) =2,24 10-4 rad. Cette valeur étant inférieure  au pouvoir séparateur de l'oeil, on ne distingue pas ces contours à l'oeil nu. ... .... 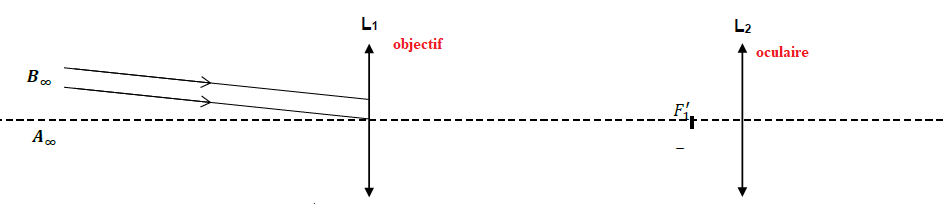Une lunette est modélisée par l’association de deux lentilles minces convergentes. 2.2. Parmi les deux lentilles utilisées, identifier celle qui joue le rôle de l’oculaire et celle qui joue le rôle de l’objectif. 2.3. Sur le schéma donné  : − construire la marche du faisceau lumineux issu du point Bꝏ considéré à l’infini au travers de la lunette ; − faire apparaître l’image intermédiaire A1B1 et l’angle a′ sous lequel est vu l’image finale A’B’ de AꝏBꝏ à travers la lunette. 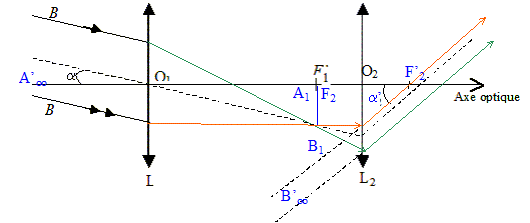2.4. Expliquer pourquoi cette lunette est qualifiée d’afocale et justifier l’intérêt de ce réglage.  Le faisceau émergent de la lunette est parallèle de même que le faisceau incident : la lunette est donc afocale. L'oeil observe sans fatigue, sans accommoder. 2.5. Exprimer le grossissement de la lunette en fonction de a et a′. G =a′ /a . On admet que le grossissement de la lunette est : G =f 'obj / f 'oc , où f 'obj et f 'oc représentent respectivement les distances focales de l’objectif et de l’oculaire. 2.6. Déterminer la valeur limite de la distance focale de l’oculaire qu’il faut associer à un objectif de distance focale 300 mm pour pouvoir distinguer l’ensemble de montagnes qui occupe le centre du cratère Tycho. Base des montagnes : 15 km. Pour les distnguer, a' doit être supérieur au pouvoir séparateur de l'oeil. a' > 2,9 10-4 rad. a = 15 / (3,844 × 105 ) =3,90 10-5 rad. G > 2,9 10-4 /(3,90 10-5 ) ; G > 7,43. f 'obj / f 'oc >7,43 ; f 'oc < 300 / 7,43 ; f 'oc < 40 mm.

menu