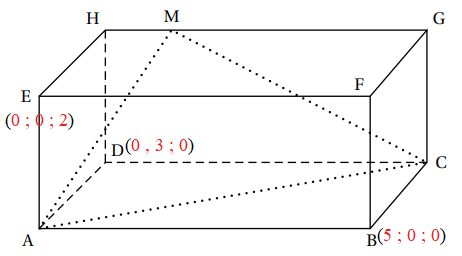
Mathématiques, géométrie dans l'espace,  Bac Amérique du Sud 9 / 2022. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... Dans la figure ci-dessous, ABCDEFGH est un parallélépipède rectangle tel que AB = 5, AD = 3 et AE = 2. L’espace est muni d’un repère orthonormé d’origine A dans lequel les points B, D et E ont respectivement pour coordonnées (5; 0; 0), (0; 3; 0) et (0; 0; 2). 1. a. Donner, dans le repère considéré, les coordonnées des points H et G. H(0 ; 3 ; 2 ) ; G(5 : 3 ; 2).  b. Donner une représentation paramétrique de la droite (GH). Coordonnées du vecteur GH : ( 5 ; 0 ; 0). Coordonnées d'un vecteur directeur de cette droite (GH) : (1 ; 0 ; 0). Par suite x = t+xH ; y = yH ; z = zH avec t réel. x = t ; y = 3 ; z = 2.  2. 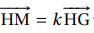Soit M un point du segment [GH] tel que  avec k un nombre réel de l’intervalle [0; 1]. a. Justifier que les coordonnées de M sont (5k ; 3 ; 2). xM-xH = k(xG-xH ) ; xM-0=k(5-0) ; xM =5 k. yM-yH = k(yG-yH ) ; yM-3=k(3-3) ; yM =3. zM-zH = k(zG-zH ) ; zM-2=k(2-2) ; zM =2.  b. En déduire la relation suivante. 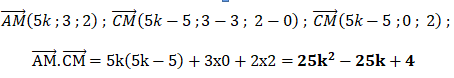 c. Déterminer les valeurs de k pour lesquelles AMC est un triangle rectangle en M. 25k2 -25k+4=0 Discriminant D = 252-4*4*25=225 = 152. k = (25+15) / 50 = 0,8 ; k = (25-15) / 50 = 0,2.  Dans toute la suite de l’exercice, on considère que le point M a pour coordonnées (1; 3; 2). On admet que le triangle AMC est rectangle en M . On rappelle que le volume d’un tétraèdre est donné par la formule 1/ 3 ×Aire de la base×h où h est la hauteur relative à la base.  3. On considère le point K de coordonnées (1; 3; 0). a. Déterminer une équation cartésienne du plan (ACD). Ce plan a pour vecteurs directeurs 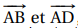. Equation cartésienne du plan (ACD), plan horizontal, z = 0. b. Justifier que le point K est le projeté orthogonal du point M sur le plan (ACD). zK = 0, donc K appartientau plan (ACD). 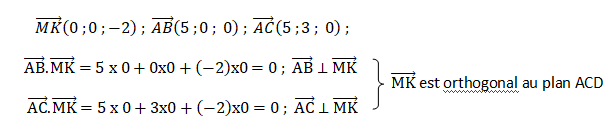Le point K est le projeté orthogonal du point M sur le plan (ACD).  c. En déduire le volume du tétraèdre MACD. Aire de base = aire du triangle rectangle ACD = AD x DC / 2 =3 x5 /2 = 7,5. Hauteur relative à cette base : MK = (02+02+(-2)2)½ = 2. Volume de ce tétraèdre : 7,5 x2 / 3 = 5 unités de volumes. 4. On note P le projeté orthogonal du point D sur le plan (AMC). Calculer la distance DP; en donner une valeur arrondie à 10−1. D sommet du tétraèdre MACD ; la base de ce tétraèdre  est le triangle AMC, rectangle en M. AM = ((1-0)2 +(3-0)2 +(2-0)2)½ = 14½. CM = ((1-5)2 +(3-3)2 +(2-0)2)½ = 20½. AM x CM / 2 = 280½ / 2 = 70½. Volume du tétraèdre : 70½ DP / 3 = 5. DP = 15 / 70½~1,8. ... .... Dans l’espace muni d’un repère orthonormé, on considère les points A(0 ; 8 ; 6), B(6 ; 4 ; 4) et C(2 ; 4 ; 0).  1. a. Justifier que les points A, B et C ne sont pas alignés. ces deux vecteurs n'étant pas colibéaires, les points A, B, c ne sont pas alignés. b. Montrer que le vecteur n de coordonnées (1 ; 2 ; −1) est un vecteur normal au plan (ABC). Le vecteur n normal à deux vecteurs non colinéaires du plan ABC est normal à ce plan.  c. Déterminer une équation cartésienne du plan (ABC). x+2y-z+d=0. B appartient à ce plan : xA+2yA-zA+d=0. 6+2*4-4+d=0 ; d = -10. x+2y-z-10=0.  2. Soient D et E les points de coordonnées respectives (0; 0; 6) et (6; 6; 0). a. Déterminer une représentation paramétrique de la droite (DE). Coordonnées du vecteur DE : ( 6 ; 6 ; -6). Coordonnées d'un vecteur directeur de cette droite ( 1 ; 1 ; -1). x = t+xD = t ; y = t +yD = t ; z = -t +zD = -t+6 avec t réel. b. Montrer que le milieu I du segment [BC] appartient à la droite (DE). Coordonnées du point I : (xB+xC) / 2 = 4 ; (yB+yC) / 2 = 4 ; (zB+zC) / 2 = 2. Si I appartient à la droite (DE) : xE = t = 4 ; yE = t = 4 ; zE = -t +6 = 2 est bien vérifié. Donc I appartient à la droite (DE).  3. On considère le triangle ABC. a. Déterminer la nature du triangle ABC. AB2 = (6-0)2 +(4-8)2 +(4-6)2 =56. AC2=(2-0)2 +(4-8)2 +(0-6)2 =56. BC2 =(2-6)2 +(4-4)2 +(0-4)2 =32. AB = AC : le triangle ABC est isocèle en A  b. Calculer l’aire du triangle ABC en unité d’aire. I est le milieu de la base BC; AI est la médiane et aussi hauteur du triangle. AI = [(4-0)2+(4-8)2 +(2-6)2]½ =48½= 4 x3½. Aire = AI x BC / 2 =4x3½ x4 x2½ / 2 = 8 x6½.  c. Calculer le produit scalaire suivant. d. En déduire une mesure de l’angle BAC arrondie à 0,1 degré. Cet angle mesure environ 44,4°.   4. On considère le point H de coordonnées ( 5/ 3 ; 10/ 3 ; -5/ 3 ) .  Montrer que H est le projeté orthogonal du point O sur le plan (ABC). En déduire la distance du point O au plan (ABC). Coordonnées du vecteur OH : (5/ 3 ; 10/ 3 ; -5/ 3 ) . Coordonnées du vecteur n orthogonal au plan (ABC) : (1 ; 2 ; -1). ces deux vecteurs sont donc colinéaires. Si H appartient au plan (ABC) :  xH+2yH-zH-10=0. 5 /3 +20 /3 -(-5 /3) -10 =0 est bien vérifiée,  donc H appartient à ce plan. OH =[(5 /3)2 +(10 / 3)2 +(-5 /3)2]½ =150½ / 3 =5 x 6½ / 3.

menu