Mathématiques, DNB Amérique du Sud 2022. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... Exercice 1 . 25 points. Voici six affirmations. Pour chacune d’entre elles, dire si elle est vraie ou fausse. On rappelle que chaque réponse doit être justifiée 1. Deux urnes opaques contiennent des boules de couleur, indiscernables au toucher. Voici la composition de chaque urne : • Urne A : 20 boules dont 8 boules bleues • Urne B : 11 boules bleues et 14 boules vertes Affirmation 1 : on a plus de chance de tirer au hasard une boule bleue dans l’urne B que dans l’urne A. Vrai. Urne A, probabilité de tirer une boule bleue : 8 / 20 = 0,4. Urne B, probabilité de tirer une boule bleue : 11 / 25 = 0,44. 2. Voici une série statistique : 14; 12; 3; 14; 7; 11; 7; 12; 14. Affirmation 2 : lamédiane de cette série statistique est 11. Faux. 3 ; 7 ; 7 ; 11 ; 12 ; 12 ; 14 ; 14 ; 14. 3. Lors d’une course à pied, un coureur a parcouru 36 km en 3 h 20. Affirmation 3 : sa vitesse moyenne est de 11,25 km/h. Faux. 3 h 20 min = 3,33 h ou 10 / 3 heures. 36 / 3,33 =36 x3 / 10 = 10,8 km / h. 4. On considère deux fonctions f et g . La fonction f est définie par : f (x) = −4x −5. Voici la représentation graphique de la fonction g : 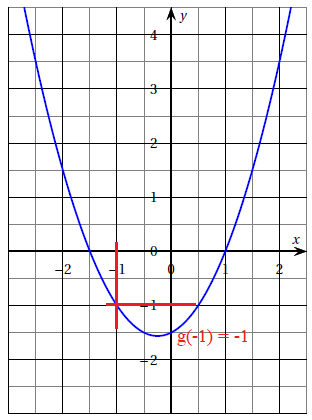Affirmation 4 : l’image de −1 par la fonction f est inférieure à l’image de −1 par la fonction g. Faux. f(-1) = -4 *(-1)-5= -1. g(-1) = -1 5. Affirmation 5 : pour tout nombre x, on a : (x +5)2−4 = (x +1)(x +9). Faux. (x +5)2−22 =(x+5+2)(x+5-2) =(x+7)(x+3). 6. On considère un carré de longueur de côté 6 mètres. Affirmation 6 : les diagonales de ce carré mesurent racine carrée(72) mètres. Vrai. Diagonale = côté fois racine carrée (2) = 6 xracine carrée (2) = racine carrée ( 6 x 6 x 2).   Exercice 2. 20 points. Le diagramme ci-dessous représente la production d’énergie solaire photovoltaïque en TWh (Térawattheure) des cinq plus gros producteurs dans l’Union européenne qui compte vingt-huit pays en 2019. 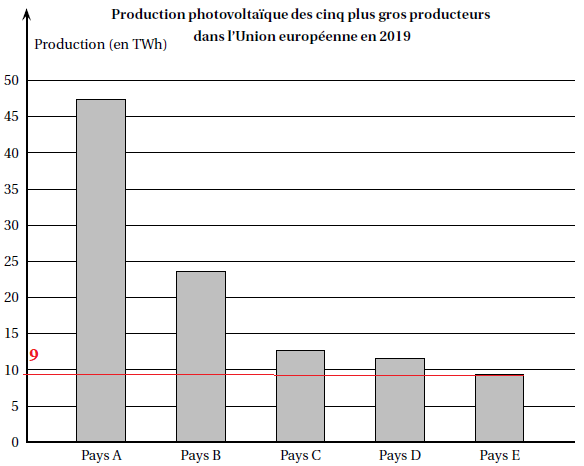1. Avec la précision permise par le graphique, donner approximativement la production photovoltaïque enTWh du pays E. 9 TWh. 2. La production photovoltaïque totale des 28 pays de l’Union européenne en 2019 est de 131,8 TWh. a. Montrer que les pays A et B totalisent à eux seuls environ 54% de la production européenne. (47 +24) / 131,8 x100 ~54 %. b. La production photovoltaïque totale des 28 pays de l’Union européenne était de 122,3 TWh en 2018. Quel est le pourcentage d’augmentation de la production photovoltaïque totale entre 2018 et 2019? Arrondir le résultat au dixième. (131,8 -122,3) / 122,3 x100 ~7,8 %. 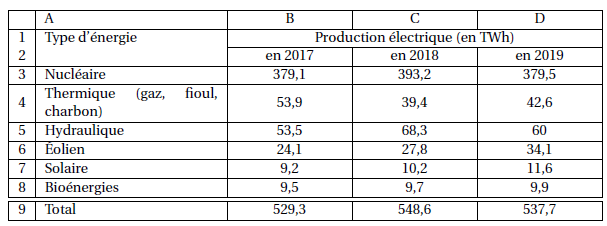3. On veut étudier dans le pays D l’évolution de la production électrique par type d’énergie de 2017 à 2019. On utilise alors le tableur pour réaliser le tableau suivant. a. Citer les types d’énergie dont la production a augmenté chaque année de 2017 à 2019. Eolien, solaire, bioénergie. b. Quelle formule a-t-on pu saisir dans la cellule B9 avant de l’étirer jusqu’à la cellule D9 ? =Somme(B3:B8). Exercice 3. 20 points Dans le triangle ADC rectangle en D, l’angle� DCA mesure 30°. Le point B est le point du segment [AC] tel que les longueurs DB et CB sont égales. La figure ci-dessous n’est pas représentée en vraie grandeur. 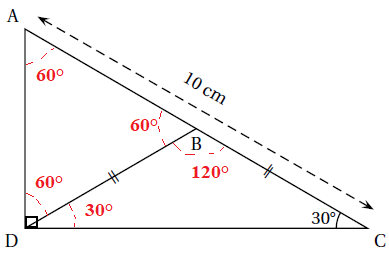1. Calculer la mesure de l’angle� DBC. 180 -30 -30 = 120°. 2. Montrer par le calcul que le segment [AD] mesure 5 cm. sin 30 = AD / AC ; AD = AC sin 30 = 10 x0,5 = 5 cm. 3. Calculer la longueur DC au millimètre près. DC2 +AD2 = AC2 ; DC2 =  AC2 -AD2 = 100 -25 = 75 ; AD = racine carrée (75) ~8,7 cm. 4. Déterminer la nature du triangle ABD. Triangle équilatéral. ... .... Exercice 4. 17 points. On souhaite réaliser le logo ci-dessous avec le logiciel Scratch à partir du script incomplet ci- dessous. 1. En mathématiques, comment appelle-t-on la transformation géométrique qui permet de passer d’un motif du logo au suivant ? Rotation. 2. Ici, le stylo est orienté horizontalement vers la droite au départ. Parmi les trois propositions suivantes, quelle est celle qui permet d’obtenir le motif souhaité ? Proposition 3. 3. Compléter le script principal en recopiant sur la copie uniquement la boucle « répéter» (c’est à- dire les instructions 4, 5, 6 et 7). 360 / 5 = 72. 4. On veut placer l’instruction ajouter 10 à la couleur du style de façon à changer de couleur à chaque motif. Sur la copie, indiquer un numéro d’instruction du script principal après laquelle on peut placer cette instruction. Placer cette instruction après l'instruction 7.  EXERCICE 5 17 points. On souhaite construire un carré potager en utilisant des planches en bois et en suivant le montage ci-dessous. Le carré potager souhaité n’a pas de fond et il a la forme d’un pavé droit de base carrée et de hauteur 30 cm.   1. À l’achat, les planches en bois mesurent 2,50 m de longueur. a. Combien de planches devra-t-on acheter ? Une planche permet de réaliser un côté. Il faut donc 4 planches. b. Déterminer le budget nécessaire (hors coût de la terre) pour réaliser ce carré potager. Planches : 4 x5,60 =22,4 €. 4 équerres : 4 x2,90 =11,6 €.  Un lot de 100 vis : 5,70 €. Total : 39,7 €. On remplit le carré potager de terre végétale au minimum jusqu’aux deux tiers de sa hauteur. On dispose la terre afin qu’elle forme un pavé droit dont la longueur du côté de la base carrée est de 118 cm. 2. Sept sacs de terre végétale seront-ils suffisants pour compléter auminimum le carré potager ? On rappelle que : 1 L = 1dm3. Volume de terre : 11,8 x11,8 x 2 =278,48 dm3. Nombre de sacs : 278,48 / 40 =6,96. 7 sacs sont suffisants.

menu