Mathématiques,
concours TSEEAC technicien supérieur de l'aviation civile 2016.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
.
.
|
..
..
......
...
|
Question 1.
Soient deux suites u et v vérifiant pour tout entier naturel n : 0 < un < vn < 2un.
A. Si 0 < un < 1, alors la suite v converge.
Contre exemple : si un = 0,5 -0,1n+1 suite croissante, majorée par 0,5 ; donc elle converge.
et si vn = 0,7 +(-0,1)n+1 :
v0 =0,6 ; v1 =0,71 ; v2 =0,699 ; v3=0,70001. La suite vn n'est ni croissante , ni décroissante, elle ne converge pas.
B. Si u converge, alors la suite v converge.
C. Si 0 < un < 1, alors la suite u converge.
Contre exemple :
si un = 0,6 +(-0,1)n+1 :
u0 =0,5 ; u1 =0,61 ; v2 =0,599 ; v3=0,60001. La suite un n'est ni croissante , ni décroissante, elle ne converge pas.
D. Si la limite en +oo de un est +oo, alors la limite en plus l'infini de vn est + oo. Vrai.
Une suite converge si elle est croissante et majorée ou si elle est décroissante et minorée.
Question 2.
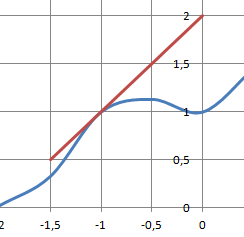
L'équation réduite de la tangente en -1 à la courbe représentant la fonction f(x) = exp(x3+x2) est :
A. 3x-2y+6=0.
B. y =x+2. Vrai
C. y=x-2.
D. -2x+2y+4=0.
f '(x) = (3x2+2x)exp(x3+x2) ; f '(-1) =1.
Equation réduite de la tangente y = x+b.
Le point de coordonnées (-1 ; f(-1) =1) appartient à la tangente :
1 = -1+b ; b = 2.
Question 3.
La valeur moyenne M de la fonction f(x) = x3+x2-x+1 sur [-1 ; 2] est :
A. 3. B. 5. C. 33 /4.
D. 11 / 4. Vrai.
Primitive de f(x) : F(x) = x4/4+x3/ 3-x2 / 2+x.
F(-1) =1 /4 -1 /3 -1 /2 -1 =(3-4-6-12) / 12 =-19 /12.
F(2) =4 +8 /3 -2 +2 =20 /3= 80 / 12.
M =(F(2) -F(-1)) / (2-(-1) =(80 +19) / 36 =11 / 4.
Question 4.
Une primitive de la fonction f définie par f(x) = x e-x est :
A. F(x) = x e-x .
On dérive en posant u = x et v = e-x ; u' = 1 et v' = -e-x.
u'v+v'u = e-x -xe-x diffère de f(x).
B. F(x) = -x e-x .
On dérive en posant u = -x et v = e-x ; u' = -1 et v' = -e-x.
u'v+v'u = -e-x +xe-x diffère de f(x).
C. F(x) =(- x-1+2 ex )e-x. Vrai.
On dérive en posant u = -x-1+2 ex et v = e-x ; u' = -1+2 ex et v' = -e-x.
u'v+v'u = (-1+2 ex)e-x -(-x-1+2 ex)e-x = xe-x = f(x).
D. (-x+1)e-x .
On dérive en posant u = -x+1 et v = e-x ; u' = -1 et v' = -e-x.
u'v+v'u = -e-x -(-x+1)e-x = (x-2) e-x diffère de f(x).
Question 5.
Soient f et g deux fonctions continues sur I = |a ; b]. On note F(x) et G(x) respectivement une primitive de f(x) et g(x).
A. Si pour tout réel x de I, on a f(x) = g(x), alors F(b)-F(a) =G(b)-G(a) Vrai.
B. Si F(b)-F(a) =G(b)-G(a), alors pour tout réel x de I, on a f(x) = g(x)
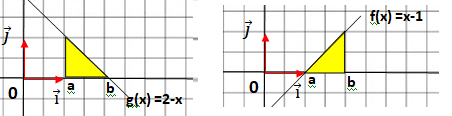 Les aires sont égales et g(x) diffère de f(x). Les aires sont égales et g(x) diffère de f(x).
C. Si pour tout réel x de I, on a f(x) < g(x), alors F(b)-F(a) < G(b)-G(a). Vrai.
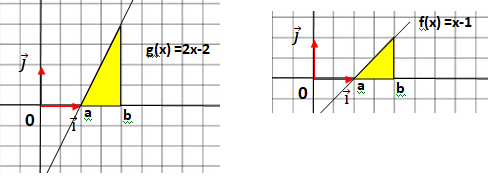
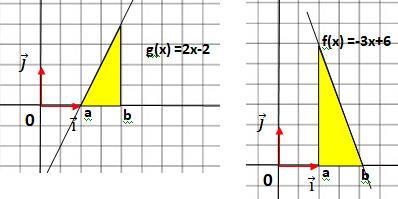
D. Si F(b)-F(a) > G(b)-G(a), alors pour tout réel x de I, on a f(x) > g(x).
Question 6.
On considère la fonction f (x) = ax2+bx+c, avec a < 0 et b2-4ac
>0. Soit S l'aire de la surface sous l'arche parabolique, comprise
entre la droite d'équation y = 0 et la courbe représentative de f.
A. S vaut la tiers de la base multipliée par la hauteur de l'arche.
B. S vaut la moitié de la base multipliée par la hauteur de l'arche.
C. S vaut les deux tiers de la base multipliée par la hauteur de l'arche. Vrai.
D. S vaut les trois quarts de la base multipliée par la hauteur de l'arche.
Par exemple : f(x) = -x2+2x+3 ; racines x1 =-1 et x2 = 3. La base vaut 3 -(-1) = 4.
f '(x) = -2x+2 s'annule pour x = 1 ; f(1) = 4 = hauteur de l'arche.
Primitive de f(x) : F(x) = -x3 / 3 +x2+3x.
Aire sous l'arche : S=F(3) -F(-1) = (-9+9+9)-(1 /3+1-3)=9+5 /3 = 32 /3.
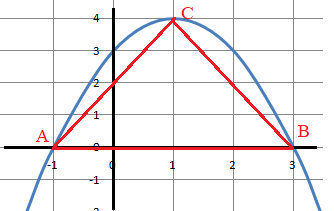 S = 4 / 3 aire du triangle ABC. S = 4 / 3 aire du triangle ABC.
Question 7.
Soit z =-3½+i.
A. z2013 est un imaginaire pur. Vrai.
|z|=(3+1)½ =2.
z / |z| = -3½ /2+i /2= cos (5p/6) + i sin (5p/6).
z = 2 exp( i 5p/6).
z2013 = 22013 exp( i 5*2013p/6) =22013 exp( i 5*2013p/6).
5*2013 p / 6 =1678 p - p /2.
z2013 =22013 exp( -i p / 2).
B. z2014 est un imaginaire pur.
5*2014 p / 6 =1678 p + p /3.
z2014 =22014 exp( i p / 3).
C. z2015 est un réel.
5*2015 p / 6 =1678 p +7 p /6.
z2015 =22015 exp( i 7p / 6).
D. z2016 est un réel. Vrai.
5*2016 p / 6 =1680 p
z2016 =22016 .
Question 8.
L'ensemble S des solutions danns C de l'équation (z-8) / (z-3)= z est :
A. {2+2i}
B. {2-2i}
C. {2+2i ; -2+2i}
D. aucune solution.
z-8 = z(z-3) ; z2-3z=z-8 ; z2-4z+8= 0.
Discriminant D = 16-32= -16 = (4i)2.
Solutions : z1 = (4+4i) /2 =2+2i et z1 = (4-4i) /2 =2-2i.
S = {2+2i ; 2-2i}
E. Aucune des réponses proposées.
|
...
|
....
|
Question
9.
Soient
A, B et O les points d'affixes respectives 1, i et 0. l'ensemble des
points M d'affixe z vérifiant |z-1|=| conjugué de z +i| est :
A. La droite (AB).
B. La médiatrice du segment [AB].
C. Le cercle de centre O et de rayon 1.
D. Le cercle de diamètre [AB].
z = x+iy ; |z-1| = |x-1+iy| =[(x-1)2 +y2]½.
| conjugué de z +i| =|x+i(1-y)| =[(1-y)2 +x2]½.
(x-1)2 +y2 =(1-y)2 +x2 ;
x2-2x+1 +y2 =y2-2y+1 +x2 soit y = x.
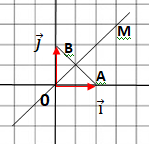
Question 10.
Soient les points A(2 ; 0 ; 3) et B (-1 ; 2 ; 0), et la droite (D) de représentation paramétrique :
x = 4+2u ; y = 1-u ; z = -2+u avec u réel.
A. Les droites (AB) et (D) ne sont pas coplanaires. Vrai.
B. Les droites (AB) et (D) sont coplanaires.
C. Les droites (AB) et (D) sont sécantes.
D. Les droites (AB) et (D) sont parallèles.
Coordonnées du vecteur AB : ( -3 ; 2 ; -3).
Coordonnées du vecteur directeur de la droite (D) : (2 ; -1 ; 1).
Ces deux vecteurs n'étant pas colinéaires, les droites (AB) et (D) sont parallèles.
Hypothèse : les droites sont sécantes.
Représentation paramétrique de la droite (AB) :
x =xA-3t ; y =yA+2t ; z =zA-3t avec t réel.
x =2-3t ; y =2t ; z =3-3t.
Par suite : 2-3t =4+2u soit 2u=-3t-2 ; u = -1,5 t -1.
Repport dans y : 1-u =1+1,5 t+1 = 1,5 t+2 diffère de 2t.
Repport dans z : -2+u = -2-1,5 t-1 = -1,5 t-3 diffère de 3-3t.
Les droites ne sont pas sécantes ; de plus elles ne sont pas parallèles : donc elles ne sont pas coplanaires.
Question 11.
SABDC est une pyramide de base carrée ABDC. Les points I, J et K sont les milieux respectifs des segments [SA], [SB] et [BD], et O désigne le centre du carré ABDC.
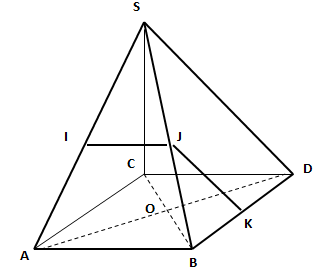
A. L'ensemble des points M tels que 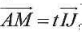 avec t réel est la droite (AD). avec t réel est la droite (AD).
Ces deux vecteurs sont colinéaires ; (IJ) droite des milieux dans le
triangle ABS : les droites (AB) et (IJ) sont parallèles.
M appartient donc à la droite (AB).
B. L'ensemble des points M tels que 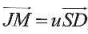 avec u réel est la droite (JK). Vrai. avec u réel est la droite (JK). Vrai.
Ces
deux vecteurs sont colinéaires ; (JK) droite des milieux dans le
triangle DBS : les droites (DS) et (JK) sont parallèles.
M appartient donc à la droite (JK).
C. L'ensemble des points M tels que 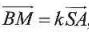 avec k réel est la droite (BJ). avec k réel est la droite (BJ).
Ces deux vecteurs sont colinéaires ; M appartient à une droite parallèle à (SA) et passant par B.
D. L'ensemble des points M tels que 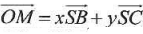 avec x et y réels est le plan (ABC). avec x et y réels est le plan (ABC).
Ces trois vecteurs sont coplanaires ; ils appartiennent au plan (SBC).
Question 12.
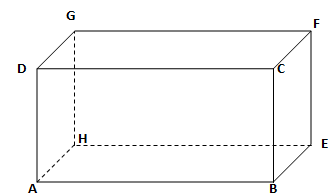
A. Si deux droites de l'espace sont perpendiculaires à une même troisième, elles sont parallèles entre elles.
Les droites (AD) et (BE) sont perpendiculaires à la droite (AB), mais elles ne sont pas parallèles.
B. Si deux droites de l'espace sont parallèles à une même troisième, elles sont parallèles entre elles. Vrai.
C. Si deux droites de l'espace sont parallèles, elles admettent une droite perpendiculaire à elles deux.
Les droites (AB) et (FG) sont parallèles, mais elles n'admettent pas une droite perpendiculaire à elles deux.
D. Si deux droites de l'espace sont parallèles à une même troisième, elles sont coplanaires. Vrai.
Question 13.
Soit X une variable aléatoire qui prend des valeurs positives. On suppose que P(1 < X < 3)=3 / 8.
Si X suit une loi uniforme sur [0 ; N], alors on a :
A. N = 5,3.
B. N = 8.
C. N = 6 / 8.
D. N = 16 / 3. Vrai.
P(1 < X < 3)=(3-1) / (N-0) =2 / N =3 / 8.
N = 16 / 3.
Question 14.
Soit X une variable aléatoire qui prend des valeurs positives. On suppose que P(1 < X < 3)=3 / 8.
Si X suit une loi exponentielle de paramètre l > 0, alors :
A. l = -ln 2.
B. l prend deux valeurs dont la valeur ln 2. Vrai.
C. l = ln(( 13½+1) / 4)
D. Il n'existe pas de tel l.
P(X < 1 )= 1-e-l ; P(X < 3 )= 1-e-3 l ; P(1 < X < 3)=1-e-3 l -(1-e-l )= e-l -e-3 l =3 / 8.
On pose Y =e-l > 0.
Y-Y3=3 / 8 ; Y3- Y+3 /8 = 0.
Y = 0,5 est une racine évidente.
(Y-0,5) ( Y2 +aY -0,75)=0.
Y3 +(a-0,5)Y2+(-0,75-0,5a) Y +3 /8=0.
On identifie a = 0,5.
Y2 +0,5Y -0,75=0 ; discriminant D =0,25+3=3,25=13 /4.
On retient la racine positive Y = (-0,5 +13½ / 2) / 2 =(-1+13½) / 4.
Par suite l = -ln (0,5) = ln 2 et -ln((-1+13½) / 4).
Question 15.
SoitX une variable aléatoire d'espérance 10 et de variance 8. Si X suit une loi binomiale de paramètre n et p, alors :
A. n = 20 et p = 0,5.
B. n = 25 et p = 0,4.
C. n = 40 et p = 0,25.
D. n = 50 et p = 0,2. Vrai.
E = np = 10 et n p(1-p) = 8.
10(1-p) = 8 ; 1-p = 0,8 ; p = 0,2 et n = 10 / 0,2 = 50.
|
|
|
|