Mathématiques,
concours TSEEAC technicien supérieur de l'aviation civile 2018.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
.
.
|
..
..
......
...
|
Partie I.
Pour tout nombre complexe z =x+iy , on note 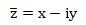 son conjugué. son conjugué.
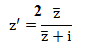
Question 1.
z' est un nombre réel si et seulement si :
A. z est imaginaire pur différent de i ; B. z est imaginaire pur vrai ; C. z est différent de 1 ; D. z est réel.
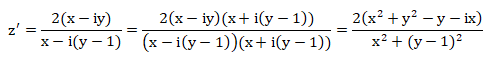 z' est un réel si x=0. Donc si z = iy.
z' est un réel si x=0. Donc si z = iy.
Question 2.
On montre que :
A. Pour z différent de -i, |z'-2| = 2 /|z+i|.
B. Pour z différent de -i, |z'-2| = 2 /|x-iy+i|. Vrai.
C. Pour z différent de i, |z'-2| = 2 /|z-i|. Vrai.
D. Pour z différent de -i, |z'-2| = 2 /|x-iy-i|.
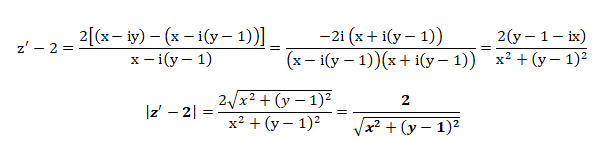
z+i=x+i(y+1) ; |z+i| = [x 2+(y+1) 2] ½.
2 / |z+i| =2 / [x2+(y+1)2]½.
|x-iy+i|= [x2+(y-1)2]½.
2 / |x-iy+i| = 2 / [x2+(y-1)2]½.
z-i = x+i(y-1) ; |z-i| = [x2+(y-1)2]½.
2 / |z-i| =2 / [x2+(y-1)2]½.
|x-iy-i| = [x2+(y+1)2]½.
2 / |x-iy-i| =2 / [x2+(y+1)2]½.
Question 3.
arg(z'-2) existe pour tout :
A. z appartenant à C. B. z appartenant à C / {i} vrai. C. z appartenant à C /{i,2}. D. z appartenant à C {i,2,-i}.
z'-2= 2[(y-1)-ix] / [x2+(1-y)2].
Le dénominateur ne doit pas être nul soit x=0 et y=1. Le point M d'affixe i est donc exclu.
Question 4.
Lorsque les arguments en question sont définis, on montre que :
A. arg(z'-2) =p /2 -arg(z-i) +2kp, k appartenant à Z.
B. arg(z'-2) =p /2 +arg(z-i) +2kp, k appartenant à Z.
C. arg(z'-2) = -p /2 +arg(z+i) +2kp, k appartenant à Z.
D. arg(z'-2) = -p /2 +arg(z-i) +2kp, k appartenant à Z.
z'-2= -2i / [x+i(1-y)]
arg(z'-2)= arg(-i) - arg(x-iy +i)= -p /2 -arg(x-iy +i).
E aucune des réponses proposées.
Question 5.
Une écriture exponentielle du nombre complexe (6½-i 2½) / (1-i) est :
A. 2 exp(-ip /12).
B. 2 exp(-i 5p /12).
C. 2*2½ exp(ip /12).
D. 2 exp(ip /12). Vrai.
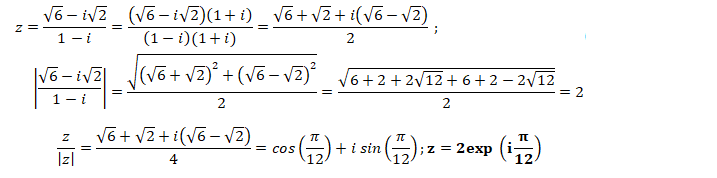
Question 6.
La forme algébrique suivante est :
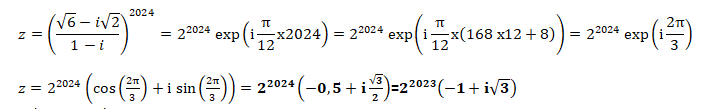 Réponse C.
Réponse C.
Question 7.
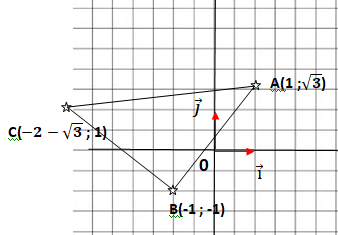
On considère les points A, B et C d'affixe respectives :
zA =1+i 3½ ; zB = -1-i ; zC = -(2+3½)+i.
Le triangle ABC est :
A. Rectangle isocèle en A.
B. Isocèle en C.
C. Equilatéral.
D. Rectangle isocèle en B. Vrai.
AB = | zB-zA| =[(-2)2 +(-1-3½)2]½ =(4+1+3+2*3½)½ = (8+2*3½)½ .
AC = | zC-zA| =[(-3-3½)2 +(1-3½)2]½ =(9+3+6*3½+1+3-2*3½)½ =(16+4*3½)½ .
BC = | zC-zB| =[(-1-3½)2 +(1+1)2]½ =(1+3+2*3½+4)½ = (8+2*3½)½ .
AB = BC ; le triangle ABC est isocèle en B.
AB2 + BC2 =8+2*3½ +8+2*3½ =16+4*3½ = AC2.
Partie II.
On définit la suite (un) par : ln(2nun) = n avec n entier naturel. De plus e ~2,718.
Question 8.
(un) est une suite géométrique :
A. de raison e et de premier terme 2 ;
B. de raison 2e et de premier terme 1 ;
C. de raison 0,5e et de premier terme 2 ;
D. de raison e et de premier terme 1.
2nun = en ; un = en / 2n =(e /2)n.
u0 = (e /2)0=1 ; u1 = (e /2)1=e / 2 ; u2 = (e /2)2=e / 2 u1.
(un) est une suite géométrique de raison e /2 et de premier terme 1.
E. aucune des réponses proposées.
Question 9.
On en déduit que la limite de un en plus l'infini est :
A. moins l'infini.
B. plus l'infini. Vrai.
C. 2 /(1-e).
D. zéro.
e / 2 > 1 ; (e /2)n tend vers plus l'infini si n tend vers plus l'infini.
Question 10.
On note Sn = u0 +u1 +...+un. On montre que :
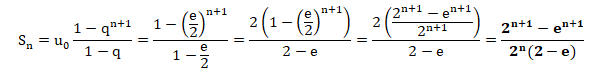
Somme des n+1 termes d'une suite géométrique de premier terme u0=1 et de raison e / 2. Réponse A.
Question 11.
On en déduit que la limite de Sn en plus l'infini est :
A. moins l'infini.
B. 2 /(1-e).
C. 2 /(e-1).
D. plus l'infini. Vrai.
Si n tend vers plus l'infini :
e / 2 > 1 ; (e / 2)n+1 tend vers plus l'infini ;
1-(e / 2)n+1 tend vers moins l'infini ;
2-e < 0 ; Sn tend vers plus l'infini.
Question 12.
On montre que si un > 1000, alors :
un =(e / 2)n > 1000 ; ln ((e / 2)n ) > ln (1000).
n ln(e/2) > ln (103) ; n ( ln(e) -ln(2)) >3 ln (10) ;
n > 3 ln (10) / (1-ln(2)).
Réponse B.
Question 13.
On note v0 = 9 ; v1 = 0,9 ; v2 = 0,09 ....
La suite (vn) est géométrique de premier terme 9 et de raison 0,1=1 / 10.
Réponses A et C.
Question 14.
On note v = v0 +v1 +...+vn. On montre que :
v=v0 (1-0,1n+1) / (1-0,1)= 9(1-0,1n+1) / 0,9 =10(1-0,1n+1) =10(1-1/10n+1)=10-10 /10n+1=10-1 / 10n.
Somme des n+1 termes d'une suite géométrique de premier terme v0=9 et de raison 0,1.
E. aucune des réponses proposées.
Question 15.
On considère le nombre réel suivant v = 9,99999....( infinité de 9 après la virgule).
Et ainsi :
A. v = 9 ; B. v =0 ; C. v = 10 vrai ; D. v =1.
v =10-1 / 10n.
Quand n tend vers plus l'infini : 1 / 10n=0,1n tend vers zéro et v tend vers 10.
|
...
|
....
|
Partie III.
Question 16.
On considère le polynome P(x) = 2x3+11 x2-20x+7. On démontre que :
A. P(x)=(x+1)(2x2+13x-7) ;
P(x= -1)= -2+11+20+7=36 différent de zéro ; x= -1 n'est pas une racine de P(x).
B. P(x)=(x+1)(2x2-13x-7) ;
C. P(x)=(x-1)(2x2-13x-7) ;
P(x=1)=2+11-20+7=0 ; x=1 est une racine de P(x).
On effectue : 2x3-13x2-7x-2x2+13x+7= 2x3-15 x2+6x+7 diffère de P(x).
D. P(x)=(x-1)(2x2+13x-7) ; vrai.
On effectue : 2x3+13x2-7x-2x2-13x+7= 2x3+11 x2-20+7 = P(x).
Question 17.
L'égalité est vraie :
A. 132=102+32 ; B. 132=102+60 +32 ; vrai . C. 152 = 225 vrai. D. 152=125.
Question 18.
(E1) 2x3+11 x2-20x+7 =0 est :
A. S1={0,5 ; -1 ; -7} ; B. S1={0,5 ; 1 ; -7} vrai . C. S1={0,5 ; 1 ; 7}. D. S1={-0,5 ; 1 ; 7}.
(x-1)(2x2+13x-7)=0.
x-1 = 0 solution x = 1.
2x2+13x-7 =0 ; discriminant D = 132+4*2*7=225=152.
Solutions x1 =(-13+15) / 4 =0,5 ; x1 =(-13-15) / 4 = -7.
Question 19.
dan R*+, l'ensemble S2 des solutions de l'équation (E2) 2(lnx)3 +11(ln x)2-20 lnx+7=0 est :
On pose X = ln x ; 2X3+11 X2-20X+7 =0.
X =1 soit x = e ; X = 0,5 soit x = e0,5 soit racine carrée (e) ; X = -7 soit x =e-7.
Réponse A.
Question 20.
Dans R, l'ensemble des solutions de l'équation 2e3x+11 e2x-20ex+7 =0 est :
On pose X = ex > 0.
2X3+11 X2-20X+7 =0.
Solutions retenues : X =0,5 soit x = ln(0,5) = - ln(2).
X =1 soit x = ln(1) = 0.
Réponse C.
Partie IV.
On donne les équations différentielles suivantes :
(F) y"+4y=0.
(G) y'+y =2e-x.
(G0) y'+y=0.
Question 21.
La fonction f solution de l'équation différentielle (F) satisfait aux conditions initiales f(0) = 3½ et f '(0) =2 est définie par l'expression :
Equation caractéristique : r2+4 = 0 soit r = ±2i.
Solutions : f(x) =A cos (2x) +Bsin(2x).
f(0) =A = 3½.
f '(x) = -2A sin(2x) +2B cos(2x).
f '(0) = 2B = 2 ; B = 1.
f(x) =3½cos(2x) +sin(2x).
Réponse A.
Question 22.
Pour tout nombre réel x nous avons :
La solution précédente peut aussi s'écrire : f(x) = A cos (2x+B), A et B étant des constantes.
f(0) = A cos B = 3½.
f '(x) =-2A sin (2x +B).
f '(0) = -2A sin (B) = 2 ; A sin (B) =-1.
tan(B) =-1/ 3½ ~ -0,577 ; B = -p/6.
Par suite A = 3½ / cos(-p/6) =2.
f(x) =2 cos (2x -p/6)= 2 sin(2x-p/6+p/2)=2 sin(2x+p / 3).
Réponse D.
Question 23.
Pour x appartenant à [0 ; 2p[, l'équation f(x) = 0 admet pour ensemble de solutions :
sin(2x+p / 3) = 0 = sin (2k p).
2x+p / 3 = 2k p ; x = -p / 6 +kp.( 5p / 6 (k=1) et 11p / 6(k=2)).
et 2x+p / 3 =(2k+1) p ; x=(k+0,5) p- p/6 . (p/3 (k=0) et 4p / 3(k=1))..
Ensemble des solutions :{5p / 6 , 11p / 6 , p/3 , 4p / 3}.
E. Aucune des solutions proposées.
Question 24.
La fonction g définie sur R par est solution de l'équation (G) :
A. g(x) = 2e-x ;
g' = -2e-x ; repport dans (G) : -2e-x +2e-x = 0 diffère de 2e-x.
B. g(x) = 2xe-x ; vrai.
g' = 2(e-x -xe-x ) ; repport dans (G) : 2(e-x -xe-x )+2xe-x =2e-x.
C. g(x) = xe-x ;
g' = e-x -xe-x ) ; repport dans (G) : e-x -xe-x +2xe-x diffère de 2e-x.
D. g(x) = -2xe-x.
g' = -2(e-x -xe-x ) ; repport dans (G) : -2(e-x -xe-x )+2xe-x diffère de 2e-x.
Question 25.
La solution h de l'équation (G) qui vérifie la condition h(0)=-1 s'écrit :
A. h(x) = (2x+1)e-x ; B. h(x) = 2xe-x ; C. h(x) = (2x-1)e-x vrai ; D. h(x) = 2xe-x-e-x. Vrai.
Solution générale de (G0) : g(x) = A e-x avec A une constante.
Solution particulière de (G) : 2xe-x .
Solution générale de (G) : h(x) = A e-x +2xe-x .
h(0) =A = -1.
h(x) = -1 e-x +2xe-x =e-x (2x-1).
|
|
|
|