Mathématiques,
concours TSEEAC technicien supérieur de l'aviation civile 2019.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
.
.
|
..
..
......
...
|
Partie 1.
On désigne par (D) l'ensemble des points M d'affixe z vérifiant : z = 1-2i +eiq, q étant un nombre réel.
A. (D) est une droite passant par le point d'affixe 2-2i.
B. (D) est le cercle de centre le point d'affixe -1+2i et de rayon 1.
C. (D) est le cercle de centre le point d'affixe 1-2i et de rayon 1. Vrai.
D. (D) est le cercle de centre le point d'affixe 1-2i et de rayon 3½.
L'ensemble des points M d'affixe z vérifiant z =w +R eiq, ( R réel strictement positif, w est un nombre complexe ) est le cercle de centre W d'affixe w et de rayon R ( R = 1 et w = 1-2i dans ce cas).
Question 2.
On désigne par (E) l'ensemble des points M d'affixe z qui vérifient |z-1+i| = |z+1+2i|.
Les points A, B et C ont respectivement pour affixe : 1-i, 1+2i et -1-2i.
Précisez la phrase ou les phrases qui est ( sont) vraie(s).
A. C est un point de (E).
B. (E) est la médiatrice du segment [AB].
C. (E) est la médiatrice du segment [AC]. Vrai.
D. (E) est le cercle de diamètre [AB].
|z-zA| = |z-zC|, donc M est la médiatrice du segment [AC].
Question 3.
On considère dans l'ensemble des nombres complexes l'équation : z +|z2| = 7+i. Cette équation admet :
A. Deux solutions distinctes qui ont pour partie imaginaire 1. Vrai.
B. Une solution réelle.
C. Deux solutions dont une seule a pour partie imaginaire 1.
D. Une solution qui a pour partie imaginaire 2.
z = x + iy avec x et y réels.
x+iy +x2+y2 = 7+i.
On identifie : iy = i soit y = 1.
x2+y2 +x =7 ; x2+1 +x =7 ; x2 +x -6=0.
Discriminant D =1+4*6 = 25 = 52.
x1 =(-1 +5) / 2 = 2 ; x2 =(-1 -5) / 2 = -3.
Par suite z1 = 2+i ; z2 = -3+i.
Partie 2.
Question 4.
On considère les points A(1 ; 2 ; -1), B(1 ; 1 ; 0), C(9 ; -1 ; -2) et S(1 ; 1 ; 1).
Précisez la phrase ou les phrases qui est ( sont) vraie(s).
A. Une équation cartésienne du plan (ABC) est : -x-2y-2z+3=0. Vrai.
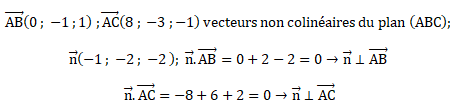
Equation de ce plan : -x-2y-2z+d=0.
B appartient à ce plan :-1-2+d=0 ; d = 3.
B. Une équation cartésienne du plan (ABC) est : x+2y+2z+3=0.
C. Une équation paramétrique de la droite (AB) est : x=-1 ; y=-2-t ; z = 1+t avec t réel.
D. Une équation paramétrique de la droite (AB) est : x= 1 ; y= 2-2t ; z = -1+2t avec t réel.
Le vecteur de coordonnées (0 ; -1 1) est un vecteur directeur de cette droite (AB) :
x =xA =1 ; y = -t+yA = -t+2 ; z =t +zA =t-1avec t réel.
Question 5.
Les coordonnées du point S' symétrique du point S par rapport au plan (ABC) sont :
A. 8 /9 ; 7 /9 ; 7 /9 ; B. 5 /9 ; 1 /9 ; 1 /9 vrai ; C. 7 /9 ; 5 /9 ; 5 /9 ; D. 1/9 ; 5 /9 ; 5 / 9.
(SS') orthogonal au plan (ABC).
xS'-xS =xS'-1=-k avec k réel ; xS'= -k+1.
yS'-yS =yS'-1=-2k ; yS'= -2k+1.
zS'-zS =zS'-1=-2k ; zS'= -2k+1.
De plus le milieu I de [S S'] appartient au plan.
Coordonnées du point I : (-k /2+1) ; -k+1 ; -k+1).
-xI-2yI-2zI+3=0.
k/2-1 +2k-2+2k-2+3=0 soit k =2 /4,5 =4 / 9.
S' (5 / 9 ; 1 /9 ; 1 /9).
Question 6.
Le triangle ABC est :
A. équilatéral ; B. isocèle ; C. rectangle en A ; D. rectangle en C.
AB2 = 0 +(-1)2+12 = 2.
AC2 = 82 +(-3)2+(-1)2 = 74.
BC2 = 82 +(-2)2+(-2)2 = 72.
AC2 =BC2 +AB2 , le triangle ABC est rectangle en B.
Partie 3.
On dispose de deux urnes U1 et U2 contenant des boules indiscernables au toucher.
U1 contient k boules blanches ( k entier supérieur ou égal à 1) et 3 boules noires.
U2 contient 2 boules blanches et une boule noire.
On tire une boule au hasard dans U1 et on la place dans U2.
On tire ensuite au hasard, une boule dans U2.
L'ensemble de ces opérations constitue une épreuve E.
On note B1 ( respectivement N1) l'événement :
On a tiré une boule blanche ( respectivement noire) dans U1 et P(B1) ( respectivement P(N1)) les probabilités associées.
On note B2 ( respectivement N2) l'événement :
On a tiré une boule blanche ( respectivement noire) dans U2 et P(B2) ( respectivement P(N2)) les probabilités associées.
Question 7.
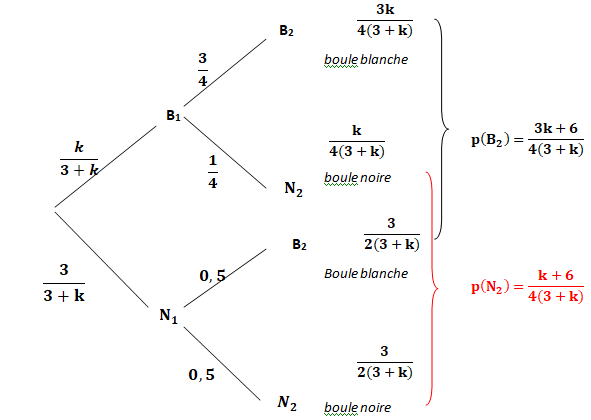
Le calcul de P(B2) donne :
A. 1 / 2. B. 3 /4. C. (3k+6) / (4k+7). D. (3k+6) / (4k+12). Vrai.
Question 8.
Le calcul de P(N2) donne :
A. 1 / 2. B. 1 /4. C. (k+1) / (4k+7). D. (k+18) / (4k+12).
Question 9.
Un joueur mise 8 € et effectue une épreuve E.
Soit X la variable aléatoire égale à la somme relative dont il dispose
à la fin de l'épreuve. Si à la fin de l'épreuve, le joueur tire une
boule blanche, il reçoit 12 € de la banque. Sinon il ne reçoit rien et
sa mise revient à la banque. Nous avons alors :
A. X appartient à { -8 ; 4 }.
B. X appartient à [ -8 ; 4 ]. Vrai.
C. X appartient à [ -8 ; 12 ].
D. X appartient à { -8 ; 12 }.
Question 10.
Précisez la phrase qui est vraie ou les phrases qui sont vraies :
A.
Le jeu est favorable au joueur à partir de 7 boules blanches au total
c'est à dire en comptant les boules blanches des deux urnes.
B. Le
jeu est favorable au joueur pour un maximum de 7 boules blanches au total
c'est à dire en comptant les boules blanches des deux urnes.
C. Le
jeu est favorable au joueur à partir de 9 boules blanches au total
c'est à dire en comptant les boules blanches des deux urnes. Vrai.
D. Le
jeu est favorable à la banque pour un maximum de 5 boules blanches au total
c'est à dire en comptant les boules blanches des deux urnes.
Loi de X :
Valeur de X
|
4
|
-8
|
Probabilité
|
(3k+6) / (4k+12). |
(k+6) / (4k+12). |
gain relatif
|
(3k+6) /(k+4)
|
-2(k+6) / (k+4)
|
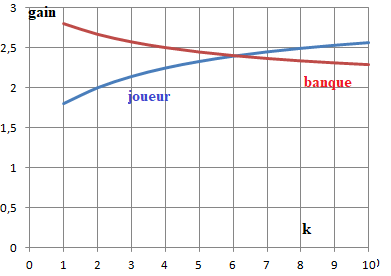
Ou comparer 3k+6 et 2(k+6). Egalité de gain pour k = 6.
Jeu favorable au joueur si 3k+6 > 2k+12 ; soit k > 6. k
Le joueur gagne plus que la banque si k > 6 ( nombre total de boules blanches > 9).
La banque gagne plus que le joueur si k < 6 ( nombre total de boules blanches < 7).
.
|
...
|
....
|
Partie 4. Suite.
Soit la suite (In) définie pour n entier naturel par :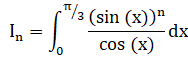
Question 11.
Le calcul suivant donne :
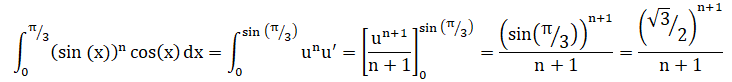
Réponse D.
Question 12.
On en déduit que In+2-In est égal à :
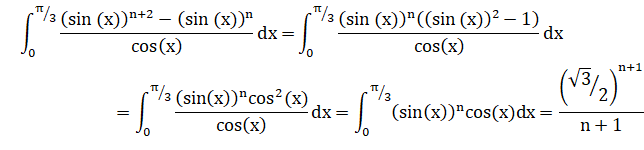
Réponse D.
Question 13.
On obtient alors :
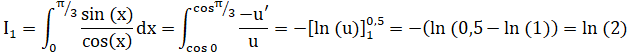
I3-I1 =3 / 8 ; I3 = 3 / 8 +ln(2).
I5-I3 =9 / 64 ; I5 = 9 / 64 +3 / 8 +ln(2) = 33 / 64 +ln(2).
E. Aucune des réponses proposées.
Question 14.
Soit f la fonction définie sur |0 ; p/3] par : f(x) = ln [tan (0,5 x +p/4)]. La dérivée f '(x) est :
On pose w = 0,5 x +p/4 ; w' = 0,5.
tan w = sin w / cos w ; on pose =u = sin w et v = cos w ; u' =w' cos w ; v' = -w' sin w.
(tan w ) ' = ( w' cos 2 w +w' sin2 w) / cos2w = w' / cos2w =0,5 /.cos2(0,5 x +p/4).
Dérivée de ln(tan w) : (tan w) ' / tan w soit :[0,5 /.cos2(0,5 x +p/4)] / tan (0,5 x +p/4).
0,5 / (cos (0,5 x +p/4) sin (0,5 x +p/4))= 1 / sin(x +p/2) =1 / cos x.
Réponse D.
.
Question 15.
On admet que a+b diffère de p/2 +kp avec k appartenant à Z.
tan ( a+b) = (tan a +tan b) / (1-tan a x tan b).
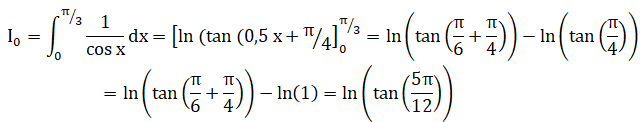
I2-I0 =3½ / 2 ; I2 =3½ / 2 + ln(tan(5p /12)).
I4-I2 =(3½ )3/ 3 =3½; I4 =3½ +3½ / 2 + ln(tan(5p /12)).
E. Aucune des réponses proposées.
|
|