Mathématiques,
Bts groupe C Métropole
2022.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Exercice
1. 9 points
Une entreprise réalise des pieds de lit en bois. La hauteur du pied est de 13 cm et sa base a pour diamètre 4 cm. Partie A - Résolution d’une
équation différentielle.
On considère l'équation différentielle (E) : 16 y" +8y' +y = 0.
1. Résoudre
l’équation 16r 2 +8r +1 = 0. Discriminant D = 8 2-4 *16 = 0.
x = -8 / 32 = -0,25.
2. Résoudre (E).
y(t) = (At + B) e -0,25t avec A et B des constantes.
3. Déterminer la fonction g solution de (E) qui vérifie g(0) =2 et g'(0)=1,5.
g(0) =2 = B.
Calcul de g'(t) en posant u =At, v = e-0,25t ; u' = A ; v' = -0,25 e-0,25t.
u'v+v'u = Ae-0,25t( 1-0,25t).
g'(0) = A = 1,5.
g(t) = (1,5t+2)e-0,25t.
Partie B. Etude de fonction.
Pour modéliser ce pied, on effectue la rotation autour de l'axe des
abscisses sur l'intervalle [0 ; 13 ] de la courbe représentative d'une
fonction f(x) = (ax+b)e -0,25t où a et b sont des réels.
L'abscisse x représente la hauteur à partir du sol en cm du pied
de lit et f(x) le rayon en cm du pied à la hauteur x. La courbe Cf passe par le point A(0 ; 2).
Le coefficient directeur de la tangente à la courbe en A vaut 1,5.
1. Justifier que b = 2.
f(0) = (0+b)e0=2 ; b=2.
2. Donner l'expression de f '(t).
On dérive f(t) en posant u =at+2, v = e-0,25t ; u' = a ; v' = -0,25 e-0,25t.
u'v+v'u = e-0,25t( a-0,25(at+2)).
3. Déterminer la valeur de a.
Le coefficient directeur de la tangente en A est f '(0)= a -0,5= 1,5 ; a = 2.
4. Modèle de la courbe ci-dessous f(x) = (2x+2)e -0,25x.
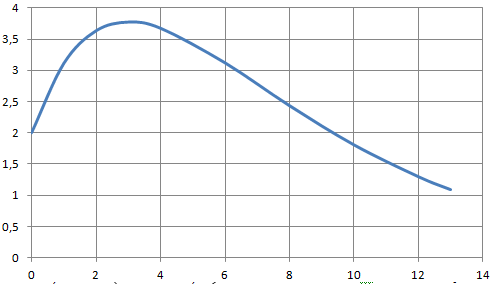
Le rayon de la partie bombée du pied correspond à la valeur maximale de
f (x). Peut-on utiliser un morceau de bois de largeur 5 cm, de mongueur
15 cm et de hauteur 7 cm pour construire ce pied ?
Le graphique indique environ 3,8 cm pour le maximum.
Par calcul : on dérive f(t) en posant u =2x+2, v = e-0,25t ; u' = 2 ; v' = -0,25 e-0,25t.
u'v+v'u = e-0,25t( 2-0,25(2x+2)) =e-0,25t(1,5-0,5x)
La dérivée s'annule pour x = 3.
f(3)=8e-0,75 =3,78.
Le morceau de bois convient.
Partie C. Calcul intégral.
Le volume du solide engendré par la rotation de la courbe Cf autour de
l'axe des abscisses sur l'intervalle [0 ; 13] est donné en cm 3 par : 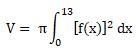
A l'aide de la calculatrice, donner une valeur approchée de V.
V = 316,90 cm 3.
|
...
|
....
|
Exercice 2. 11 points
Partie A - Probabilités
conditionnelles
L’entreprise réalise des pièces en bois avec 2 machines A et B qui fabriquent respectivement 60 % et 40 % des pièces.
3% des pièces fabriquées par A sont défectueuses.
2% des pièces fabriquées par B sont défectueuses.
On
définit les évènements suivants :
• A : « la pièce provient de la machine A»;
• B : « la pièce provient de la machine B »;
• D : « la pièce présente un défaut ».
1. Calculer PA(D) et PB(D).
PA(D) = 0,03.
PB(D) = 0,02.
2. Calculer la
probabilité que la pièce soit défectueuse et ait été produite par la machine A.
P(A n D) = =0,60 x0,03 = 0,018.
3. Calculer P(D).
P(D)
= P(A n D) + P(B n D) =0,018 +0,02 x0,40 =0,026.
Partie B. Lois de probabilités.
Un magasin commande un lot de 400 pièces. On note X la variable
aléatoire qui, à tout lot de 400 pièces, associe le nombre de pièce
présentant un défaut.
1. Déterminer la loi suivie par X ainsi que ses paramètres.
C'est un schéma de bernoulli. : on répète 400 expériences aléatoires ayant deux issues, identiques et indépendantes entre elles.
X suit la loi binomiale de paramètre n = 400 et p =0,026.
2. Calculer la probabilité d'avoir au plus 6 pièces défectueuses.
P(X < 6) ~0,104 ( donné par la calculatrice).
3. Montrer que la probabilité d'avoir au moins 7 pièces défectueuses est 0,896.
P(X > 7) = 1 -P(X < 6) = 1-0,104 = 0,896.
4. On admet que l'on peut approcher la loi suivie par la variable X par une loi de Poisson de paramètre l. On appelle Y la variable qui suit cette loi. Justifier que l = 10,4.
l = n p =400 x 0,026=10,4.
5. Déterminer la valeur arrondie à 10-3 de l'erreur commise par cette approximation.
La calculatrice donne P(Z > 7) = 0,893.
Erreur commise : 0,896 -0,893 = 0,003.
Partie C - Test d'hypothèse
La
scierie qui fournit le bois affirme que 85 % de morceaux pris au hasard
dans la production, sont conformes en largeur et en longueur.
L'entreprise fait un test bilatéral au seuil de risque de 5 % pour
vérifier cette affirmation.
On note H0 : p = 0,85.
On appelle F la variable aléatoire qui, à tout échantillon de 100
morceaux de bois, associe la fréquence des morceaux conformes en
largeur et en longueur. On admet que sous H0, la variable aléayoire F suit la loi normale de moyenne 0,85 et d'écart type (0,85 x0,15 / 100)½=0,036.
1.Preciser l'hypothèse alternative H1 du test.
H1 : p diffère de 0,85.
2. Déterminer la zone d'acceptation du test.
Intervalle de confiance [0,85 -1,96 x0,036 ; 0,85 +1,96 x0,036) soit [0,78 ;
0,92].
3.
Sur un échantillon de 100 morceaux de bois, on compte 80 morceaux
conformes en lageur et longueur. L'entreprise a t-elle raison de douter
de l'affirmation de la scierie ?
Fréquence des morceaux non conformes : f = 80 /100 = 0,8.
0,8 est situé dans l'intervalle d'acceptation. L'entreprise ne peut pas remettre en cause l'affirmation de la scierie.
|
|