Aller sur Mars par l'orbite de Hohmann, concours Capes 2022. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . .. .. ...... ... Dans une approche simplifiée : - les orbites terrestre et martienne sont considérées comme circulaires ; - sauf indication contraire, on néglige l'attraction gravitationnelle exercée par la Terre  sur la sonde et l'attraction exercée par Mars sur la sonde. La sonde n'est soumise qu'à l'attraction de gravitation exercée par le Soleil ; - la sonde quitte l'orbite terrestre à l'instant t1 et rejoint l'orbite martienne à l'instant t2. Dt = t2-t1, la durée de transfert ; - à l'instant t1, Mars est en M1, la Terre en T1 et la sonde est au voisnange de la Terre quasiment en T1 ; les propulseurs de la sonde sont alors allumés pendant une durée très courte devant Dt. 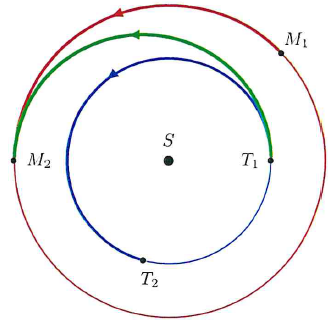Cela confère à la sonde un incrément de vitesse qui la place sur une orbite lui permettant de rejoindre Mars ; - pendant le voyage de T1 à M2, la sonde n'utilise pas ses propulseurs. Elle se trouve sur une orbite de transfert élliptique ayant T1 comme périhélie et M2 comme aphélie. Cette trajectoire s'appelle " orbite de Hohmann" ; - à l'instant t2 la sonde arrive au voisinage de Mars ( point M2), les propulseurs de la sonde sont à nouveau allumés pendant une durée très courte devant Dt. La sonde a un incrément de vitesse qui la place sur une orbite martienne. Le soleil est en S. Q16. Qu'est ce qu'un référentiel galiléen ? Définir le référentiel héliocentrique, le référentiel géocentrique, et le référentiel terrestre. Citer une manifestation du caractère non galiléen du référentiel géocentrique, et une manifestation du caractère non galiléen du référentiel terrestre. Le principe d'inertie  (" si les forces qui s'appliquent sur un système se compensent, alors le système est animé d'un mouvement rectiligne uniforme ") s'applique dans un référentiel est galiléen . Référentiel héliocentrique : l'origine est le centre du Soleil et les tois axes pointent vers des étoiles fixes. Référentiel géocentrique : l'origine est le centre de la Terre et les tois axes pointent vers des étoiles fixes. Référentiel terrestre : origine à la surface de la terre et les trois axes sont fixes par rapport à  la Terre. Manifestation du caractère non galiléen du référentiel géocentrique : marée d'origine solaire ou lunaire. Manifestation du caractère non galiléen du référentiel terrestre : apparition d'une force de Coriolis qui dévie tout objet en mouvement par rapport à la Terre, vers la droite dans l'émisphère nord et vers la gauche dans l'émisphère sud. Dans les questions suivantes, on se place dans le référentiel héliocentrique.  Q17. On considère une planète de période de révolution T autour du Soleil de masse MS. Elle décrit un cercle de rayon a et  de centre S. Justifier que la trajectoire circulaire de la planète est nécessairement uniforme. 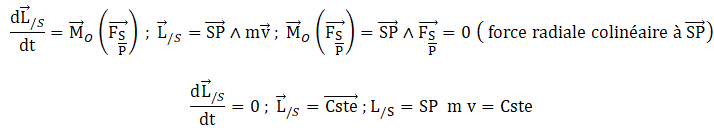Théorème du moment cinétique appliqué à la planète P de masse m dans le référentiel héliocentrique noté RS : Ou bien : la force gravitationnelle perpendiculaire à la vitesse, ne travaille pas. Le théorème de l'énergie cinétique  implique une énergie cinétique et une vitesse constantes. Démontrer la troisième loi de Kepler. On note : r :rayon de l'orbite de la planète ; a : accélération de cette planète. La planète décrit la circonférence 2 pr à la vitesse v pendant la durée T. 2 pr = v T ; 4 p2 r2 = v2 T2. Or v2 = GMS / r ; par suite : 4 p2 r2 = GMS / r T2. T2 / r3 = 4 p2 / (GMS). On admet qu'elle se généralise à une trajectoire elliptique de demi-grand axe a. Q18. La durée de l'année terrestre est TT =  ; distance Terre Soleil : RST =1,50 1011 m; distance Soleil Mars : RSM =2,3 1011 m.  Estimer la durée du transfert de la Terre à Mars. L'orbite de transfert est la moitié d'une ellipse dont la Soleil est l'un des foyers. Son demi-grand axe est a = (RST +RSM) / 2=0,5 ( 1,50 1011+2,3 1011) =1,9 1011 m. La sonde parcourt cette distance en une demi-période T. T2 = 4 p2 a3 / (GMS). T2 / 4 = p2 a3 / (GMS). T / 2 = p [a3 / (GMS)]½ =3,14 [(1,9 1011)3 / (1,99 1030 x6,67 10-11)]½ ~23 106 s ou 270 jours. ... .... Q19. Justifier la phrase " ces missions profitent d'une fenètre de lancement vers la planète rouge qui ne s'ouvre que tous les 26 mois"   Période de révolution de Mars : TM2 = 4 p2 RSM3 / (GMS) ; TM= 2 x3,14 [(2,3 1011)3 / (1,99 1030 x6,67 10-11)]½ ~60 106 s ou 23 mois terrestres. Vitesse angulaire de Mars : 360° / 23 ~ 16° / mois. Vitesse angulaire de la  Terre : 360° / 12 ~ 30° / mois. Soit une date favorable au lancement : la terre lors du lancement est alignée avec la position de Mars à l'arrivée de la sonde (T1, S et M2 alignés). Cela signifie un même écart angulaire entre la Terre et Mars. 360 / (30-16) ~26 mois. Q 20. L'éjection de carburant par la fusée permet sa propulsion. Sur quel principe mécanique est basé ce phénomène ? Comment l'illustrer ? Principes des actions réciproques. Illustrations de ce principe : tir d'un boulet par un canon, d'une balle par un fusil ; propulsion d'un ballon de baudruche par éjection d'air Q21. Au départ, la vitesse vT1 de la sonde est pratiquement égale à la vitesse de la Terre sur son orbite. Montrer que cette vitesse est : vT1 =[2pMSG / TT]1 /3. D'après la question 17 : 2 p r T = vT1 TT1 ; TT1  = 2 p r T / vT1 ; 1/  r T =  2 p / (vT1TT1) . et TT12 / r T3 =4p2 / (GMS). TT12(2 p)3 / (vT1TT1)3  =4p2 / (GMS). (2 p / (vT1 3 TT1) =1 / (GMS). vT1 = [2 pGMS/ TT1]1/3 =[ 2 x3,14 x6,67 10-11 x1,99 1030) / (365x24x3600)]1/3 ~2,98 104 m/s. Q22. On admet que l'énergie mécanique de la sonde de masse m sur l'orbite de Hohmann est Em = -0,5 G m MS / aH, où aH est le demi-grand axe de la trajectoire élliptique associée. Déterminer v 'T1 , vitesse de la sonde sur l’orbite de Hohmann au point T1, juste après le transfert de la sonde de l’orbite terrestre à l’orbite de Hohmann. Energie potentielle de gravitation au périhélie : Ep = -G m MS / RST. Em = -0,5 G m MS / aH =0,5 m v 'T12 -G m MS / RST. -G  MS / aH = v 'T12 - 2G  MS / RST. v 'T12 =G  MS (2 / RST-1/aH) v 'T12 =6,67 10-11 x1,99 1030 [ 2/ (150 109) -1 /(1,99 1011)] =1,07 109 ; v 'T1 =3,27 104 m /s. Quel est l’incrément de vitesse permettant le passage de l’orbite terrestre à l’orbite de Hohmann ? On fera l’application numérique. v 'T1 -vT1=3,27 104 -2,98 104 = 2,9 103 m /s. Avec ce modèle, l’incrément total de vitesse à donner pour le voyage aller est de 5,5km · s−1. À quel autre moment de la trajectoire faut-il fournir un incrément de vitesse, et donc entraîner une consommation de carburant ? A l'aphélie, il faut fournir un autre incrément de vitesse à la sonde afin que sa vitesse atteigne celle de la planète Mars. Quelle interaction nécessitant une consommation de carburant supplémentaire n’a pas été prise en compte ? Lors du lancement, il faut extraire la sonde du champ de gravitation terrestre en atteignant la vitesse de libération.

menu