Transport
et distribution d'énergie électrique,
concours CAPLP maths sciences 2022
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
Le
propriétaire d’une villa envisage l’installation d’une piscine chauffée
assez éloignée de son habitation. Afin d’alimenter la pompe de
filtration et la pompe à chaleur, une ligne d’alimentation électrique
monophasée doit être déployée depuis le tableau principal de la villa
jusqu’au local technique accolé à la piscine.
Le technicien chargé du projet doit dimensionner la section des câbles
de cette ligne (2,5 mm² ou 6 mm²) en prenant en compte trois critères :
le coût d’installation (plus élevé pour une large section), les pertes
en ligne et la consommation électrique des pompes.
La longueur de chaque câble est estimée à 50 m et le dossier technique
(schéma électrique et caractéristiques des pompes) est donné.
Problématique :
Quelle est la section des câbles la plus adaptée conformément à la
norme NF C 15-100 ?
Partie 1 : Appropriation de la situation
professionnelle par une étude physique.
L’objectif de cette partie est de s’approprier la situation
professionnelle en la simplifiant de la façon suivante :
- la capacité linéique des câbles et les pertes diélectriques sont
négligées ;
- les contraintes de démarrage des moteurs (intensités et facteurs de
puissance) ne sont pas prises en compte ;
- la chute de tension correspond à la valeur efficace de DU (voir schéma ci-dessous).
Ces simplifications n’ont aucune conséquence sur le résultat attendu.
Le schéma équivalent du circuit est :
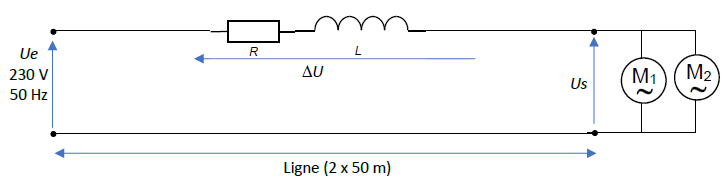
R représente la résistance de la ligne et L son inductance.
M1 désigne le moteur de la pompe à filtration et M2
le moteur de la pompe à chaleur.
1. Montrer à partir
de la loi d’Ohm locale, que pour un conducteur rectiligne de section S,
de longueur L et soumis à une tension u,
on a R = r L / S où r représente la
résistivité, en W.m,
du conducteur.
La relation qui lie la densité de courant
J au
champ électrique E dépend de la conductivité du milieu : c'est la loi
d'Ohm locale ( J = s
E ) où entre deux points M1
et M2
:

où dl est équivalent à un
déplacement dx selon la direction ex
entre M1 et M2
et où n
est le vecteur normal au point M1 ici.
On connaît plus la loi
d'Ohm macroscopique où l'on définit la
résistance qui lie la tension et l'intensité. Cette loi s'écrit U = RI
mais la valeur de R peut être parfois complexe à calculer. Néanmoins si
on considère que le conducteur est un cylindre de section S et de
longueur L entre les points M1 et M2,
sa formule est assez simple car R = U / I.
Dans le cas
d'un conducteur cylindrique la formule permettant de
calculer la résistance en fonction de s, L et S.
U = E L ; I = J S et J = s E. Par suite : I
= s E S et R = U
/ I =
L
/ ( s
S)= r L
/ S.
s :
conductivité ( S m-1) ; L : longueur (m) ; S :
section (m2) ; R résistance (ohm W).
2. On s’appuiera
sur les documents 1.2 et 1.3. Calculer R, en W, et L, en H, pour des
câbles en cuivre ayant des conducteurs de section 2,5 mm² ou 6 mm².
Bien
qu’utilisant du câble à trois conducteurs, on considèrera la valeur de
a d’un câble à deux conducteurs (le fil de terre ne transporte pas
d’énergie électrique en fonctionnement normal).
r = 2,2 10-8 W m ; R2,5 =2,2 10-8
x 100 / (2,5 10-6)=0,88 ohm
; R6 =2,2 10-8 x 100 /
(6 10-6)~0,37 ohm.
L =0,05 +ln( 2a/ r) en µH / m avec a = r+1 mm et r rayon du câble.
Section 2,5 mm2 : r ~0,892 mm ; L =0,05 +ln(3,78 / 0,892
)~1,5 µH / m ; L = 1,5 10-4 H.
Section
6 mm2 : r ~1,38 mm ; L =0,05 +ln(4,76 / 1,38 )~1,24 µH / m ;
L ~ 1,2 10-4 H.
3. Montrer, en calculant le facteur
de puissance cos fL
de la ligne, que l’on peut négliger son effet inductif quel que soit,
parmi les deux valeurs possibles, le diamètre des câbles choisi.
tan fL = L w
/ R avec w = 2 p f = 314 rad / s.
Section 2,5 mm2
: tan fL = 1,5 10-4 x314 / 0,88 ~0,054 ; cos fL ~0,999.
Section 6 mm2 : tan fL = 1,2 10-4
x314 / 0,37 ~0,102 ; cos fL ~0,995.
4. Dans un premier temps, on
néglige DU et on
a donc US
= 230 V. Calculer les puissances active, réactive et apparente totales,
notées respectivement P (en W), Q (en VAR) et S (en VA), de l’ensemble
formé par les deux moteurs (chauffage et filtration) en fonctionnements
simultanés.
Pompe de filtration
: intensité nominale chauffage 11,6 A. Pompe de filtration : I = 5,8 A.
Pompe de filtration : P =
1,1 kW ; S = 230 x 5,8 =1334 VA ; cos f =P / S = 1100 / 1334
=0,825 ; sin f =0,566 ; Q = 1100 x0,566
=623 VAR.
Pompe à chaleur : P
= 2,35 kW ; S = 230 x 11,6 =2668 VA ; cos f =P / S = 2350 / 2668 =0,880 ; sin
f
=0,473 ; Q = 2350 x0,473 =1113 VAR.
Ptotale =1,1 +2,35 = 3,45
kW.
Qtotal =623 +1113 =1736 VAR.
S2 =P2+Q2 =34502 +17362
=1,49 107 ; S = 3862 VA.
5. En déduire que
l’intensité totale I consommée par les deux moteurs est d’environ 17,4
A.
Stotal / U =3862 / 230 ~16,8 A.
6.
R étant négligeable devant la résistance équivalente des deux moteurs,
on considèrera que l’intensité du courant qui circule dans la ligne a
pour valeur I. Calculer DU,
commenter.
DU
=R2,5I =0,88 x17,4 =15 V soit 15 / 230 ~0,065 ( 6,5 %),
supérieure à 5 %..
DU =R6I =0,37
x17,4 =6,4 V soit 6,4 / 230 ~0,028 (2,8 %) négligeable dans ce cas.
7. Calculer les pertes de puissance
par effet Joule pour les deux sections de conducteurs.
R2,5I2 =0,88 x 17,42 = 266 W ; R6I2
=0,37 x 17,42 =112 W.
8.
En déduire le câble le plus adapté, sachant que le coût d’installation
(inconnu) ne saurait être prépondérant devant le respect des normes en
vigueur.
Câble 6 mm2.
Partie 2 : La situation
professionnelle en classe de première en physique-chimie.
Pour permettre aux élèves de première MÉLEC de répondre à la
problématique soulevée par la situation professionnelle, le professeur
organise une activité lors d’une séance de travaux pratiques.
9. Proposer une
expérimentation (liste du matériel, montage expérimental et protocole)
permettant d’illustrer qualitativement les pertes en ligne et la
conséquence qui en découle pour le consommateur.
10.
Préciser les points de vigilance à respecter dans l’activité que le
professeur donnerait à ses élèves (notions à ne pas aborder, formules
et valeurs à donner).
11. Lister les
questions qu’il
poserait dans cette activité (elle contient nécessairement une partie
expérimentale et les différents calculs pourront être demandés sous la
forme d’un tableau à compléter).
12. Pour chaque
question proposée à la question 11., lui associer au moins une
compétence.
La centrale électrique sera modélisée par un générateur 12 V
continu.
La ligne électrique de 100 km est modélisée par deux fils
électriques
associés chacun à une résistance R = 10 ohms.
Les habitations et les usines sont
modélisées par une simple ampoule (12V ; 250 mA).
Ampéremètre et voltmètres.
Mesurer les tensions U G, U L et l’intensité
I ligne du courant et compléter le tableau suivant :
Tension
aux bornes du générateur
|
Tension
aux bornes de la lampe
|
Intensité
du courant dans le circuit
|
Puissance
délivrée par le générateur
|
Pertes
de puissance en lignes
|
Puissance
reçue par la lempe
|
UG=
|
UL=
|
Iligne
|
PG
= UG Iligne =
|
Pperte
=
|
Plampe
=Ulampe Iligne
= |
Proposer une explication au faible éclairement de la lampe.
Comment optimiser les pertes en lignes ?
Pertes par effet Joule en ligne : R ligne I 2.
R ligne est proportionnelle à la longueur et inversement
proportionnelle à la section.
Pour une longueur fixée, augmenter la section.
Puissance = U x I ; pour une puissance donnée, augmenter la tension,
c'est faire chuter l'intensité.
Capacité :
justifier l'intérêt du transport d'énergie électrique à grande distance
sous haute tension.
Compétences
: réaliser, analyser, valider.
Partie 3 : La séquence correspondante en
classe de première en physique-chimie.
L’activité précédente a permis d’introduire la partie du programme
d’électricité « Transporter l’énergie sous forme électrique » et la
notion de pertes en ligne. Le professeur souhaite la compléter en
s’appuyant sur les questions suivantes.
13. Proposer une
exploitation pédagogique du document 3.1 et l’objectif visé. Les
approximations de ce document devront être signalées.
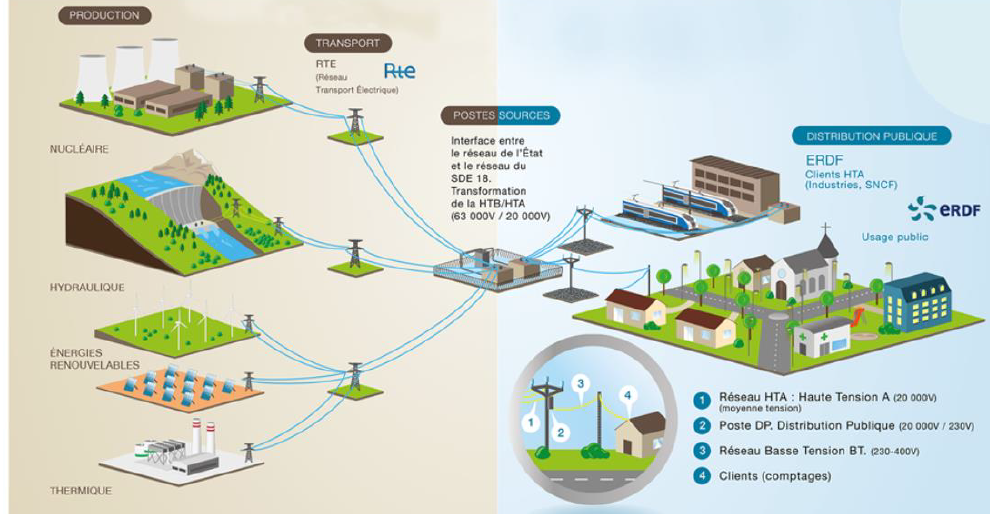
Quelle est la part des énergies renouvelables dans la production
d'énergie électrique ?
Quel est
l'intérêt du transport d'énergie électrique à grande distance sous
haute tension ?
14. Le document 3.2
est un extrait d’évaluation certificative. Les résultats expérimentaux
partiels sont donnés dans le tableau.
a. Calculer les
valeurs manquantes dans ce tableau et proposer une réponse à la
question B.6
b. Préciser les
compétences évaluables dans la question B.6.
B.3 Réaliser le montage suivant :
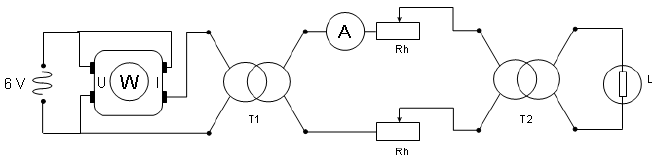
B.4 Régler le rhéostat sur R = 5 ohms et compléter la colonne 1 du
tableau en préciser les unités.
|
Mesures
avec T1 et T2.
|
Mesures
sans T1 et T2. |
Puissance
fournie par le générateur. Lue sur le wattmètre
|
PG
= 9,3 W
|
PG
= 9,3 W |
Intensité
du courant dans les lignes
lue sur l'ampèremètre.
|
I
= 0,12 A
|
I
= 0,5 A
|
Puissance
perdue par effet Joule en ligne
PJ = RI2.
|
PJ
= 2 x5 x0,122 =0,144 W
|
PJ
= 2 x5 x0,52 =2,5 W |
Rapport
des puissances ( en %)
|
PJ
/ PG =0,144 / 9,3 x100
=1,54 %
|
PJ
/ PG =2,5 / 9,3 x100
=26,9 % |
B.5 Retirer T1
et T2 du montage et compléter la collonne 2 du tableau.
B.6 Rédiger une conclusion montrant l'intérêt de transporter l'énergie
électrique à haute tension.
Pour
une puissance donnée, augmenter la tension, c'est faire chuter
l'intensité en ligne, donc l'effet joule ( pertes en lignes).
Compétences :
analyser,
valider.
15. Proposer une activité
expérimentale destinée aux élèves permettant
d’illustrer le seul rôle de T1 (montage, protocole, ce qui est attendu,
ce qu’il faut retenir).
Tension aux bornes du générateur : 9,3 / 0,5 =18,6 V. T1 transformateur
abaisseur de tension.
Matériel : un G.B.F muni
d’une fiche B.N.C. en position sinusoïdale et réglé sur la fréquence f
= 50 Hz.
Un transformateur démontable
constitué : d'une bobine de 500 spires, d'une bobine de 1000
spires, d'une culasse pour le noyau.
Un interrupteur, des fils conducteurs, un dispositif Exao avec des
capteurs voltmètre et ampèremètre.
Relever les tensions et les intensités efficaces.
Calculer les rapports U s / U p et n p / n s
et conclure.
16. Le document 3.3 reproduit une
copie d’élève. La corriger en
précisant les annotations éventuelles qu’il conviendrait de mettre sur
la copie de l’élève et les compétences évaluées lors de chaque question.


|
Partie 4 : Minimisation des pertes en ligne par effet Joule en classe de première en mathématiques.
Le professeur décide d’une exploitation en mathématiques du problème
des pertes par effet Joule en le considérant d’un point de vue plus
global : l’interconnexion en réseaux des lignes de transport depuis les
centrales de production jusqu’aux consommateurs. Pour ce faire, le
professeur s’appuie sur un modèle simplifié composé de :
deux centrales de production ;
quatre lignes de transport uniquement résistives R1, R2, R3 et R4 ;
deux villes Ville 1 et Ville 2 qui consomment une puissance constante et qui sont uniquement résistives ;
d'un noeud d’interconnexion.
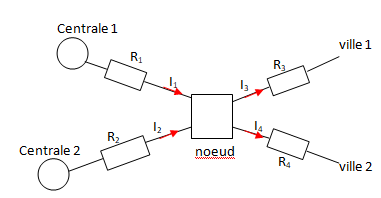
On cherche à déterminer les intensités I1 et I2 qui minimisent la puissance totale P perdue par effet Joule sur l’ensemble du réseau. Cette puissance P est égale à R1I12+R2I22+R3I32+R4I42.
Les intensités doivent satisfaire les contraintes suivantes :
0≤ I1≤ I1max et 0≤ I2≤ I2max (la capacité de production des centrales est limitée) ;
I1max+ I2max > I3+I4 (la production des centrales permet de répondre à la consommation des villes) ;
I3 et I4 sont constantes (la puissance consommée par chaque ville est constante) ;
I1+ I2= I3+ I4=K (où K est une constante).
17. Déterminer en fonction de K, I1max et I2max l’ensemble D des valeurs de I1 pour lesquelles ces contraintes sont satisfaites.
I1+ I2 < I1max+ I2max ; K < I1max+ I2max ; I1≤ I1max ;
K+I1 < 2 I1max+ I2max ; 0 < I1 < 2 I1max+ I2max -K.
18. On note Pc=R3 I32+R4 I42. Montrer que P=(R1+R2 )I12−2KR2I1+Pc+K2R2.
P =R1I12+R2I22+R3I32+R4I42 =R1I12+R2I22+Pc.
I2=K-I1 ; P =R1I12+R2(K-I1)2+Pc =R1I12+R2I12+K2R2-2KR2I1.
19. Soit f la fonction définie et dérivable sur l’ensemble D déterminé à la question 17, d’expression f(x)=(R1+R2 )x2−2KR2x+Pc+K2R2.
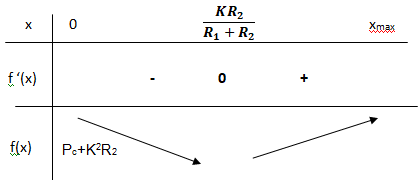
Étudier la fonction f et dresser son tableau de variations.
f '(x) =2(R1+R2 )x−2KR2 ; f '(x) = 0 si x = KR2 / (R1+R2 ).
f '(x) > 0 si x > KR2 / (R1+R2 ) et f est croissante.
f '(x) < 0 si x < KR2 / (R1+R2 ) et f est décroissante.
Dans la suite, on considère une maquette du modèle simplifié pour laquelle on a les valeurs suivantes :
R1 = 0,1 ohm ; R2 = 0,2 ohm ; R3 = 0,1 ohm ; R4 = 0,2 ohm ; I1max = 4 A ; I2max = 6 A ; I3=2 A ; I4=3 A.
20. Donner, dans ce cas, l’ensemble de définition de la fonction f et montrer que : f(x)=0,1x2+0,2(5−x)2+2,2.
0 < I1 < 2 I1max+ I2max -K.
0 < I1 < 14 -5 ; 0 < I1 < 9.
Pc =0,1 *22+0,2*32=2,2.
f(x) =0,3 x2-2x +2,2+25*0,2 =0,3 x2-2x +7,2.
0,1x2+0,2(5−x)2+2,2 =0,1x2+0,2x2+5-2x+2,2 =0,3 x2-2x +7,2.
21. Déterminer le minimum de la fonction f et préciser la valeur de x pour laquelle ce minimum est atteint.
x = 2 / 0,6 =10 /3. Minimum : 0,3 * 100 /9-2*10 /3 +7,2 =10 /
3-20 / 3 +72 /10 = -10 /3 +72 / 10 =(-100 +216) / 30 =116 / 30 ~3,87.
22. On admet que la
fonction f dont l’expression a été établie à la question 20 modélise
les pertes en ligne en fonction de l’intensité I1. Plus précisément, f(x) est la puissance, en watts, dissipée par effet Joule sur le réseau, lorsque x est l’intensité I1, en ampères,
En déduire les valeurs de I1 et I2 qui minimisent les pertes par effet Joule sur le réseau.
I1 = 116 / 30 ~3,87 A. I2 = K-I1 =5-116 / 30 =34 / 30 ~1,13 A.
23. Rédiger un
texte de présentation d’une activité et sa problématique, correspondant
à la situation étudiée, qui pourrait être proposée à des élèves de
première professionnelle MÉLEC.
Les pertes en ligne lors du transport de l'énergie électrique peuvent s'exprimées par f(x) = 0,3 x2-2x +7,2 avex apparteant à [0 ; 5 ]. Ces pertes sont minimales si x = 10 / 3.
Problématique : cette donnée est-elle correcte ?
24.
Rédiger ensuite les questions permettant de répondre à cette
problématique en indiquant pour chacune d’elles les capacités et
connaissances du module « Fonctions dérivées et études des variations
d'une fonction » mises en oeuvre.
Calculer la dérivée f '(x) ; étudier son signe et donner le tableau de variations de f(x).
25. Un commentaire
du module « Fonctions dérivées et études des variations d'une fonction
» indique « On visualise graphiquement la différence entre extremum
local et extremum global ». La fonction f étudiée dans cette partie
est-elle adaptée pour sensibiliser les élèves à cette différence ?
Justifier la réponse.
Oui. 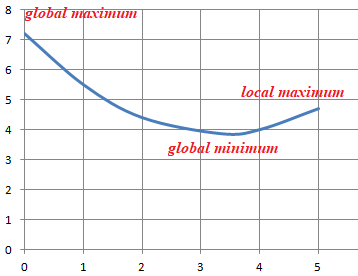
26. Un autre
commentaire de ce module indique : « La formule de dérivation de la
fonction carré est conjecturée à l’aide des outils numériques puis
admise ».
Expliquer comment à l'aide du fichier nommé « conjecture », dont une
capture d'écran est fournie sur le document 3.4, les élèves peuvent
conjecturer la formule de dérivation de la fonction carré.
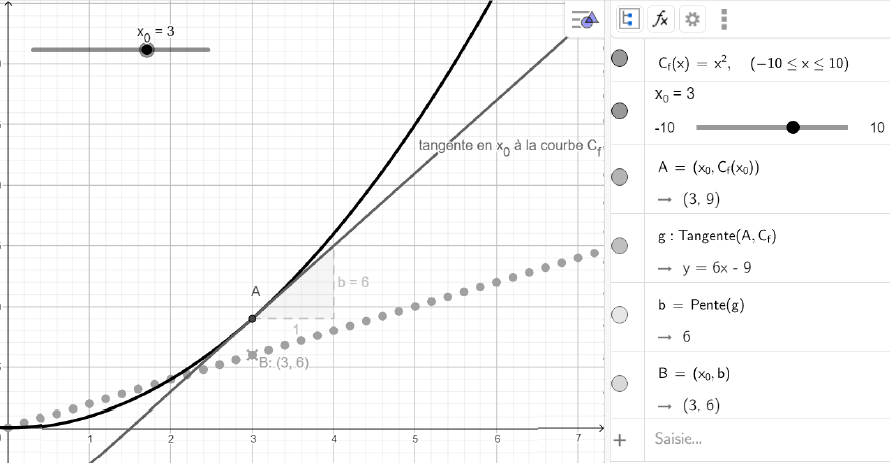
Le coefficient directeur de la tangente en un point est égal au nombre dérivée en ce même point.
Choisir différentes valeurs de x et comparer chaque valeur avec le coefficient dirceteur de la tangente à la courbe.
Partie 5 : Prolongement en classe de terminale en physique-chimie.
Le transport de l’énergie électrique à haute tension, qui met en jeu
des pylônes en acier protégés contre la corrosion, permet un
prolongement possible en classe de terminale professionnelle MÉLEC sur
le thème de la protection des métaux contre la corrosion.
27. Préciser les capacités et connaissances du programme concernant spécifiquement ce thème .
Classer expérimentalement les couples oxydant / réducteur.
Identifier l'oxydant et le réducteur dans une transformation d'oxydoréduction.
Prévoir une réaction d'oxydoréduction et protéger les métaux contre la corrosion.
28. Proposer une
séquence pédagogique portant sur ce thème, en détaillant l’ordre des
séances et en explicitant les expérimentations envisagées.
29. Présenter une
séance de travaux pratiques qui aborde d’une part la mise en évidence
du phénomène de corrosion d’un métal et d’autre part la protection
contre la corrosion d’un métal. On indiquera en particulier la
problématique, le matériel disponible, la démarche et les conclusions
attendues.
Vous disposez de trois solutions :
solution contenant des ions Cu2+ ; solution contenant des ions Zn2+ ; solution contenant des ions Fe2+
Vous disposez aussi d’échantillons de
trois métaux différents : du
fer, du cuivre et du zinc.
Tremper dans chaque solution un métal et observer.
La paille de fer se cuivre et la solution se décolore.
Test de présence d'ions dans la solution : ajout de quelques gouttes de
soude : observation d'un précipité vert caractéristique des ions Fe2+.
Lame de zinc dans la solution de sulfate de fer II :
Les ions Fe2+ disparaissent et un précipité blanc d'hydroxyde de zinc apparaît qui se dissout dans un excès de soude.
30.
Décrire les protocoles des expériences citées à la question 29, citer
les capacités du programme qu’elles permettent de développer et donner
la trace écrite correspondante, telle qu’elle pourrait figurer dans le
cahier d’un élève.
Classification électrochimique de quelques métaux ; règle du gamma. Capacités : réaliser, observer,formuler des hypothèses.
31. Le zinc protège le fer de la corrosion grâce au principe
de l’anode sacrificielle. Justifier cette affirmation.
Placer dans la boîte de Pétri trois clous entourés de tortillons de cuivre, zinc et
magnésium ;
Recouvrir les clous de la solution d’eau de Javel.
Seul le clou entouré de fil cuivre subit une oxydation ; les deux autres restent
intacts.
Le fer est attaqué lorsqu’il est associé à un métal moins réducteur que lui comme
le cuivre ; par contre, il est protégé par le zinc et le magnésium qui sont des
métaux plus réducteurs.
C’est le principe de protection du fer contre la corrosion par anode sacrificielle
32. Citer deux autres moyens de protection du fer contre la corrosion.
Revêtement du métal par des peintures, laques, films plastiques, vernis ou revêtements métalliques (nickelage, argenture, cadmiage…).
Partie 6 : Prolongement en classe de terminale en mathématiques sur le module « Trigonométrie ».
L’association en dérivation des deux moteurs (chauffage et filtration)
(voir schéma de la partie 1) est l’occasion de travailler en classe de
terminale sur le module « Trigonométrie ».
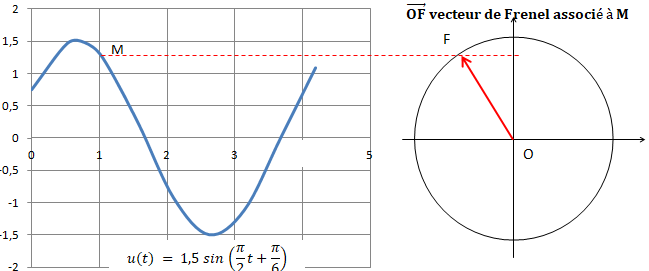
33. Proposer la
trame d’une activité permettant de développer la capacité du programme
« Établir des liens entre le vecteur de Fresnel d’une tension ou d’une
intensité sinusoïdale de la forme a sin(wt+f) et la courbe représentative de la fonction qui à t associe a sin(wt+f)».
34. En se replaçant dans les conditions de la question 5, montrer que les expressions i1(𝑡) et i2(𝑡)
des intensités des courants traversant respectivement la pompe à
filtration et la pompe à chaleur, peuvent s’écrire (en choisissant
judicieusement l’origine des temps et en arrondissant les déphasages au
centième) :
𝑖1(𝑡)= 5,8 √2sin(100pt+0,60) et 𝑖2(𝑡)=11,6 √2 sin(100p𝑡+0,49).
Pompe de filtration : sin f =0,566 ; f =0,60 rad ( 34 degrés) ; pompe à chaleur : sin
f
=0,473 ;
f
=0,49 rad. (28 degrés ).
w = 2 pf = 100 p rad /s.
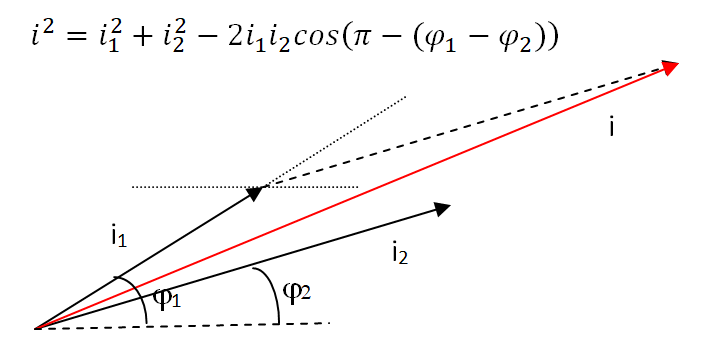
35. L’expression de l’intensité du courant dans la ligne alimentant les deux moteurs vérifie la relation :
𝑖(𝑡)=𝑖1(𝑡)+𝑖2(𝑡). En s’aidant des vecteurs de Fresnel représentant les courants 𝑖,𝑖1 et 𝑖2, déterminer l'expression de 𝑖(𝑡) en fonction de 𝑡.
Partie 7 : Conception d’une séquence d’enseignement en mathématiques portant sur le module « Trigonométrie ».
Cette séquence, destinée à des élèves de terminale professionnelle
MÉLEC, porte sur les équations de la forme cos 𝑥= 𝑎, sin𝑥=𝑏 et sin (wt+f))=𝑐 sur un intervalle donné.
36. Préciser le nombre de séances prévues et, pour chacune d’elles, la
trace écrite qui pourrait figurer dans le cahier d’un élève.
Utilise le tableau virtuel géogebra.
Exemple : cos x = 0,5 est équivalent à cos x = cos (p/3).
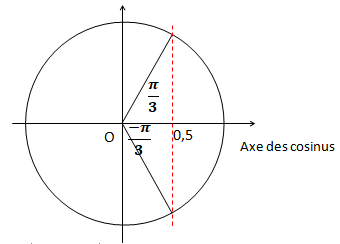 Deux solutions x = ± p/3 + 2kp. Deux solutions x = ± p/3 + 2kp.
Exemple : sin x = 0,5 est équivalent à sin x = sin (p/6).
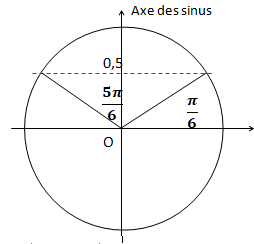 Deux solutions x = p/6 + 2kp.et x =p- p/6 + 2kp. Deux solutions x = p/6 + 2kp.et x =p- p/6 + 2kp.
37. Présenter la séance qui aborde la résolution de l’équation sin (wt+f)= 𝑐. On pourra prendre appui sur la situation professionnelle étudiée dans la partie 6.
On précisera en particulier :
- les activités proposées et les tâches attendues de l’élève ;
- l’organisation pédagogique et le rôle de l’enseignant ;
- les modalités de mise en oeuvre des outils numériques et leur plus-value.
|
|