Mathématiques,
concours recrutement professeur des écoles 2022
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
Exercice 1.
Un enseignant de moyenne section de maternelle
souhaite créer un jeu sur le modèle du jeu de l’oie pour travailler
avec ses élèves la construction du nombre et en particulier des
décompositions et recompositions de nombres de 1 à 6.
Il fabrique deux dés équilibrés selon les patrons suivants :
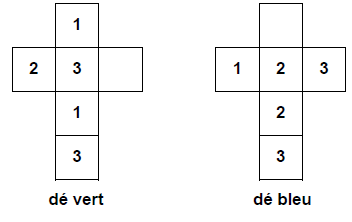
Il crée un parcours sur lequel les élèves déplacent un pion selon le
protocole suivant :
- l’élève lance les deux dés ;
- il avance son pion d’autant de cases que la somme des nombres
inscrits sur les faces supérieures des deux dés ; s’il n’obtient aucun
nombre sur les deux dés (deux faces vierges), il passe son tour.
Le plateau de jeu est matérialisé par une bande numérique comme
ci-dessous.

1. On lance le dé vert seul. Quelle est la probabilité d’obtenir 3.
2 cas favorables sur 6 cas possibles.
Probabilité d'obtenir 3 : 2 / 6 = 1 /3.
Dans la suite de l’exercice, afin de simplifier les réponses, on pourra
considérer que les faces vierges correspondent au nombre 0.
2. Un élève lance les deux dés, il calcule la somme des nombres obtenus.
a. Quelles sommes peuvent être obtenues ?
|
0
|
1
|
1
|
2
|
3
|
3
|
0
|
0
|
1
|
1
|
2
|
3
|
3
|
1
|
1
|
2
|
2
|
3
|
4
|
4
|
2
|
2
|
3
|
3
|
4
|
5
|
5
|
2
|
2
|
3
|
3
|
4
|
5
|
5
|
3
|
3
|
4
|
4
|
5
|
6
|
6
|
3
|
3
|
4
|
4
|
5
|
6
|
6
|
0 ; 1 ; 2 ; 3 ; 4 ; 5 ; 6.
b. Quelle est la probabilité qu’il doive passer son tour ?
1 cas favorable sur 36 cas possibles.
Probabilité d'obtenir deux fois zéro : 1 / 36.
c. Quelle est la probabilité qu’il doive avancer de 3 cases ?
9 cas favorables sur 36 cas possibles.
Probabilité d'avancer de trois cases : 9 / 36 = 1 / 4..
d. Déterminer la probabilité de chacun des résultats possibles.
Probabilité d'obtenir une somme égale à 1 : 3 / 36 = 1 / 12.
Probabilité d'obtenir une somme égale à 2 : 5 / 36
Probabilité d'obtenir une somme égale à 4 : 8 / 36 =2 / 9
Probabilité d'obtenir une somme égale à 5 : 6 / 36 = 1 / 6.
Probabilité d'obtenir une somme égale à 6 : 4 / 36 = 1 / 9..
e. Quelle est la probabilité que le résultat du dé vert soit
strictement supérieur à celui du dé bleu ?
(1 ; 0 ) ; (1 ; 0 ) ; (2 ; 0 ) ; (2 ; 1 ) ; (3 ; 0 ) ; (3 ; 1 ) ; (3 ; 2 ) ; (3 ; 2 ) ; (3 ; 0 ) ; (3 ; 1 ) ; (3 ; 2 ) ; (3 ; 2 ).
12 cas favorables sur 36 cas possibles : 12 / 36 = 1 / 3.
3. Après deux tours de jeu, un élève est arrivé sur la case 10 . Quelle
est la probabilité qu’il se soit arrêté sur la case 4 au premier tour ?
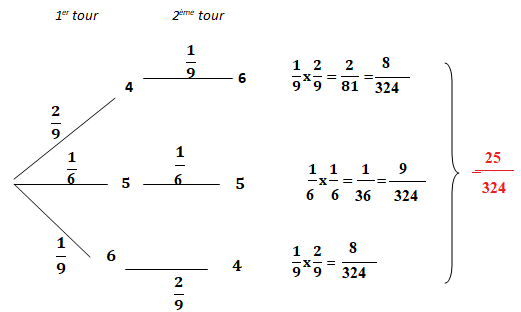
Probabilité qu’il se soit arrêté sur la case 4 au premier tour : 8 / 324 / (25 / 324) =8 / 25 =0,32.
Exercice 2.
Un nombre décimal est souvent défini de la façon suivante : « Un nombre
décimal est un nombre pouvant s’écrire sous la forme a / 10n où a est
un nombre entier et n est un nombre entier positif. ».
1. On s’appuiera sur la définition précédente pour répondre aux deux questions suivantes.
a. Montrer que 0,127 est un nombre décimal.
0,127 = 127 / 1000 = 127 / 103.
b. Montrer que 1 /4 est un nombre décimal.
1 / 4 = 0,25 = 25 / 100 = 25 / 102.
2. Dans une classe de CM2 un enseignant demande aux élèves de dire ce
qu’est un nombre décimal, voici trois réponses proposées par des élèves
:
- Élève A : « Un nombre décimal est un nombre avec une virgule. »
- Élève B : « Un nombre décimal est un nombre qui s’écrit avec une fraction qui a 10 ou 100 au dénominateur. »
- Élève C : « Un nombre décimal est un nombre qui n’est pas entier. »
Expliquer pourquoi chacune des définitions proposées ne convient pas
d’un point de vue mathématique. On pourra notamment s’appuyer sur des
contre-exemples.
A : 22 peut s'écrire 22 / 100, c'est donc un nombre décimal.
B : 0,127 = 127 / 1000 = 127 / 103. L'écriture ne contient ni 10 ni 100 au dénominateur.
C : 1 = 1 / 100, c'est un nombre entier et décimal.
3. Parmi les nombres suivants dire, en justifiant, lesquels sont
décimaux et lesquels ne le sont pas : 2,48 ; 7 /25 ; 12 ; 7 / 9 ; 49 / 14.
2,48 = 248 / 100 = 248 / 102 est un nombre décimal.
7 / 25 = 7 x4 / (25 x4) = 28 / 100 = 28 / 102 est un nombre décimal.
12 = 12 / 100 est un nombre décimal.
7 / 9 diffère de a / 10n car 10n n'est pas un multiple de 9. ( la somme des chiffres qui composent 10n est égale à 1 et non à 9 ).
49 / 14 = 7 x7 /(2 x7) = 7 / 2 = 7 x5 / (2 x5) = 35 / 101 est un nombre décimal.
4. Le produit de deux nombres décimaux est-il toujours un nombre décimal ? Justifier.
Soit deux nombres décimaux A = a / 10n et B = b / 10p.
AB = a b / 10n+p.
a b est un nombre entier car c'est le produit de deux nombres entiers.
n+p est un nombre entier positif, somme de deux nombres entiers positifs.
5. Le quotient de deux nombres décimaux est-il toujours un nombre décimal ? Justifier.
7 / 9 diffère de a / 10n car 10n n'est pas un multiple de 9.
Le quotient de deux nombres décimaux n'est pas toujours un nombre décimal.
|
Exercice 3.
PARTIE A.
Alice veut réaliser une activité avec ses élèves de petite section de
maternelle. Elle a besoin de découper 30 disques de 14 cm de rayon dans
des feuilles de dimensions 120 cm × 80 cm, c’est-à-dire de 120 cm de
longueur sur 80 cm de largeur.
Elle aimerait les dessiner en occupant l’espace de chaque feuille en
commençant en haut à gauche puis en continuant comme dans la figure
ci-dessous.
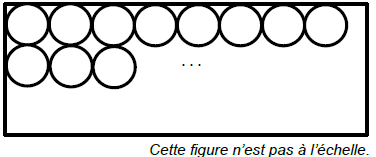
1. Calculer l’aire de la feuille, en cm².
A = 120 x 80 =9,6 103 cm2.
2. a. Expliquer pourquoi Alice peut tracer au maximum 4 disques dans la longueur de la feuille.
Diamètre d'un disque : 28 cm ; 28 x4 = 112 cm, inférieure à 120 cm.
28 x5 = 140 cm, supérieure à 120 cm.
b. En déduire le nombre maximum de disques qu’elle pourra tracer dans cette feuille.
28 x 2 =56 cm ; 28 x3 = 82 cm supérieur à 80 cm.
Donc 2 rangées de 4 disques soit 8 disques.
c. Combien faut-il au minimum de feuilles pour dessiner les 30 disques ?
30 / 8 =3,75 donc il faut 4 feuilles.
3. Représenter à l'échelle 1/8 une feuille de dimensions 120 cm × 80 cm avec les disques qu'elle peut contenir.
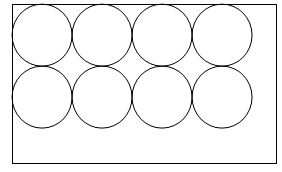
4. Calculer l’aire exacte d’un disque puis donner la valeur arrondie au centimètre carré près.
pR2 = p x 142 =196 p ~ 616 cm2.
Dans la suite du problème, on considèrera que l’aire d’un disque est de 616 cm².
5. a. Quelle est l’aire de papier non utilisé si Alice découpe 8 disques dans une feuille ?
Aire de 8 disques : 8 x 616 =4928 cm2.
Aire de la feuille : 9600 cm2.
Aire de papier non utilisé : 9600 -4928 =4672 cm2.
Quelle proportion, exprimée en pourcentage et arrondie à l’unité de
pourcentage, de l’aire totale de la feuille cela représente-t-il ?
4672 / 9600 ~0,49 ( 49 %).
b. Quelle est l’aire de papier non utilisé après avoir découpé 30 disques ?
3 feuilles avec 8 disques : aire de papier non utilisée : 4672 x3 =14 016 cm2.
Une feuille avec 6 disques : 9600 -6 x616 =5904 cm2.
Total : 19 920 cm2.
Quelle proportion, exprimée en pourcentage et arrondie à l’unité de
pourcentage, de l’aire totale des feuilles utilisées cela
représente-t-il ?
19 920 / (4x9600)~0,52 (52 %).
6. Pour limiter le
gaspillage de papier, Alice veut choisir le format qui permettra
d’obtenir le moins de chutes (en cm²) tout en gardant la même
disposition que précédemment. Elle a le choix entre plusieurs formats
proposés par un fournisseur :
Raisin : 65 cm × 50 cm.
Jésus : 75 cm × 56 cm.
Imperial : 80 cm × 60 cm.
Grand Aigle : 105 cm × 75 cm.
Grand Monde : 120 cm × 80 cm.
Pour obtenir les 30 disques, le format Grand Aigle permet-il d’obtenir
moins de chutes (en cm²) que le format Grand Monde ? Justifier la
réponse.
Grand Aigle : 105 / 28=3,75 soit 3 disques par longueur.
75 / 28 =2,68 soit 2 disques par largeur.
Soit 5 feuilles.
Aire de 6 disques : 6 x 616 =3696 cm2.
Aire de la feuille : 105 x75 =7875 cm2.
Aire de papier non utilisé : 5 x(7875 -3696) =20 895 cm2.
Le format Grand Aigle ne permet pas d’obtenir
moins de chutes.
PARTIE B.
D’autres classes veulent réaliser la même activité. La directrice se
demande quel format permettra d’obtenir moins de chutes en fonction du
nombre de disques à découper.
Pour cela, elle utilise un tableur :
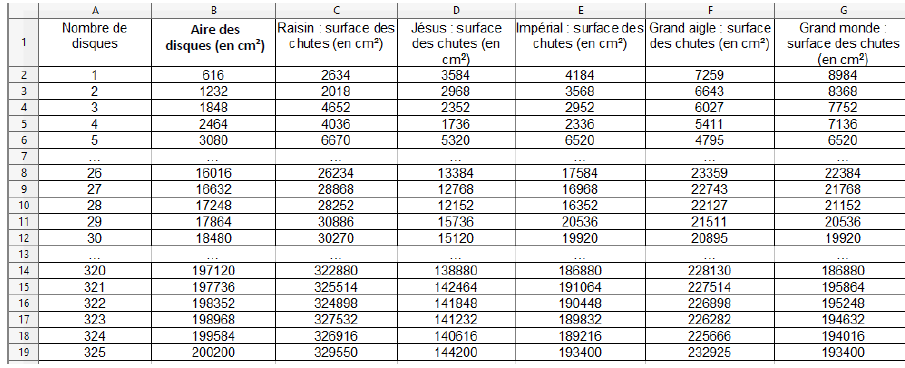
1. Sans justifier, donner la formule qui a été saisie dans la cellule B2 et étirée vers le bas.
= A2*616
2. Sans justifier, donner le format permettant d’éviter au mieux le gaspillage de papier si l’on veut réaliser 325 disques.
Jésus.
3. Les deux seuls
fournisseurs disponibles ne disposent plus que de feuilles au format «
Grand Monde ». La directrice veut choisir le fournisseur qui propose le
tarif le plus avantageux pour acheter les feuilles nécessaires à la
réalisation des disques. On a représenté graphiquement ci-dessous le
prix en fonction du nombre de feuilles commandées chez chaque
fournisseur :
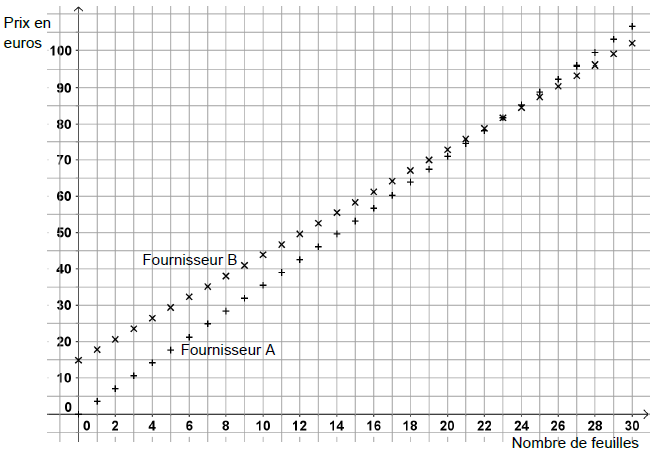
a. Chez un des deux
fournisseurs le coût des feuilles est proportionnel au nombre de
feuilles achetées. Lequel ? On justifiera la réponse.
Fournisseur A : le graphe est une droite passant par l'origine.
Répondre aux questions suivantes par lecture graphique, sans justifier.
b. Quel est le prix que va coûter l’achat de 15 feuilles chez chaque fournisseur ?
A : 54 € ; B : 58 €.
c. Déterminer le nombre maximal de feuilles que l’on peut acheter chez chaque fournisseur si l’on dispose d’un budget de 45 €.
A : 12 ; B : 10.
d. À partir de combien de feuilles est-il plus avantageux de commander chez le fournisseur B ?
Intersection des deux courbes : 23 feuilles.
4. On a maintenant représenté sous forme de tableau les tarifs proposés par chaque fournisseur :
Coût d’une feuille (en €) : A 3,55 € port gratuit.
B : 2,90 € port 14,90 €.
a. Quel est le prix que va coûter l’achat de 15 feuilles chez chaque fournisseur ?
A : 15 x3,55 =53,25 €.
B : 2,90 x15 +14,90 =58,4 €.
b. Déterminer le nombre de feuilles que l’on peut acheter chez chaque fournisseur si l’on dispose d’un budget de 312 €.
A : 312 / 3,55 ~ 87 feuilles.
B : 312 -14,90 =297,1 ; 297,1 / 2,90 ~102 feuilles.
c. À partir de combien de feuilles est-il plus avantageux de commander chez le fournisseur B ? Justifier la réponse.,90.
On note x le nombre de feuilles.
A : 3,55 x ; B : 2,90 x+14,90.
3,55x < 2,90 x +14,90 ;
0,65 x <14,90 ; x < 23.
A partir de 23 feuilles, B est le plus avantageux.
d. Sachant qu’il y
a 325 disques à dessiner et que l’on peut en mettre 8 par feuille,
quelle entreprise la directrice va-t-elle choisir ? Quel sera le prix
de cette commande ?
325 / 8 =40,625 donc 41 feuilles.
Fournisseur B : 41 x 2,90 +14,90 =133,8 €.
PARTIE C.
1. Après avoir
découpé les 30 disques, Alice veut les border d’un fil de laine. Quelle
longueur de laine devra-t-elle utiliser pour border tous les disques ?
On donnera le résultat en mètre, arrondi au décimètre.
Périmètre d'un disque : 2 p R = 2 x14 x3,14 =87,96 cm = 0,8796 m..
Longueur de fil : 0,8796 x30 ~26,4 m.
2. Alice met 48
minutes à dessiner et découper les 30 disques alors que son collègue
Bertrand met 1 heure et 12 minutes à effectuer cette tâche.
a. Donner le temps moyen que met Alice pour découper un disque (en minutes et secondes).
48 / 30 =1,6 min = 1 min 36 s = 96 s.
b. Combien de temps mettront-ils pour découper les 30 disques ensemble ? Donner le résultat en minute et seconde.
Bertrand découpe un disque en : (3600+12x60) / 30=144 s.
Durée de la découpe t : t / 96 +t /144 =30.
1,5 t / 144 + t /144 = 30.
2,5 t =30 x144 ; t =1728 s =28 min 48 s. .
|
|