Eau
de javel, analyse, optique, thermodynamique, viscosité,
concours ITRF Grenoble Alpes 2019.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
.
.
|
..
..
......
...
|
Eau de Javel commerciale : propriétés,
dosage.
A. Propriétés d'une eau de Javel commerciale.
L'eau de Javel est une solution aqueuse équimolaire d'hypochlorite de
sodium (Na+ aq + ClO- aq) et de chlorure de
sodium (Na+ aq + Cl- aq). La concentration des
eaux de Javel est exprimée par la teneur en chlore actif sous la forme
d'un pourcentage pondéral.
Ce pourcentage correspond à la masse, exprimée en gramme de dichlore Cl2(g),
nécessaire pour préparer 100 g de
solution, selon l'équation bilan :
Cl2(g) + 2HO-aq --> ClO- aq + Cl-
aq + H2O.
La terminologie « eau de Javel » est réservée aux solutions vendues
dans le commerce dont la teneur en chlore actif est inférieure à 10 %.
Pour les teneurs plus élevées, dans l'industrie, on utilise la
dénomination " hypochlorite de sodium".
1. Quels types de
renseignements sont donnés par les phrases H et P d'une fiche
toxicologique ?
Phrases H : dangers encourus, phrases de risques.
Phrases P : précautions recommandées, conseils de prudence.
L'ajout d'acide chlorhydrique à une solution d'eau de Javel provoque un
dégagement de dichlore gazeux. On désigne le degré chlorométrique d'une
solution concentrée d'eau de Javel comme le volume exprimé en litre de
dichlore gazeux qui peut être libéré par l'addition d'acide
chlorhydrique en quantité non limitante à un litre d'eau de Javel dans
les conditions normales de température et de pression (273,0 K et 1,013
bar).
On cherche la correspondance entre le degré chlorométrique et le
pourcentage en chlore actif d'une solution commerciale d'eau de Javel à
9,6 %.
On donne la densité de la solution d = 1,158 et M(Cl) = 35,50 g.mol-1.
2. Écrire
l'équation bilan de la réaction entre une eau de Javel et une solution
d'acide chlorhydrique. On indiquera les couples oxydant/réducteur.
Cl2(g) / Cl-aq ; ClO-aq / Cl2(g).
ClO-aq
+Cl-aq
+ 2H+aq --> Cl2(g) + H2O(l).
3. Calculer la
quantité de matière de dichlore dissous dans 100g de solution. En
déduire la concentration en ions hypochlorite de la solution.
9,6 g de dichlore pour préparer 100 g de solution.
n(Cl2) = 9,6 / 71 = 0,1351 ~0,14 mol.
Volume de la solution : 100 / 1,158 =86,36 mL.
[ClO-aq]
=0,1351 / 0,08636 ~1,56 mol / L.
4. Calculer le
degré chlorométrique de la solution commerciale.
V =
n(Cl2)
RT / P = 1,56 x 8,314 x273 / (1,013 105)={3,5 10-2
m3 = 35 litres = 35 degrés chlorométrique.
B. Dosage d'une solution
d'eau de Javel commerciale.
Principe de la
manipulation :
Les ions hypochlorite ClO- aq réagissent avec les ions
arsénite AsO2- aq en excès selon :
ClO- aq + AsO2- aq + H2O =
Cl-aq+ 2H+aq + AsO43- aq (1)
L'excès d'ions arsénite est alors titré par une solution de diiode
selon :
I2 aq + AsO2- aq + 2H2O = 2 I-aq+4H+aq
+ AsO43- aq (2).
Réactifs et
solutions à disposition :
Hydrogénocarbonate de sodium solide HCO3Na (s) ; solution
commerciale d'eau de Javel à 9,6 % en chlore actif.
Solution d'arsénite de sodium de concentration c1 = 5,00.10-2
mol.L-1.
Solution de diiode de concentration c2 = 5,00.10-2
mol.L-1 ; empois d'amidon.
Protocole
opératoire :
Dans un premier temps, on place un volume V1 = 10,0 mL de la
solution d'ions arsénite de concentration c1
inconnue dans un bécher, on y ajoute 40,0 mL d'eau ; 0,50 g
d'hydrogénocarbonate de sodium solide et un peu d'empois d'amidon.
D'une burette, on doit verser VE1 = 9,60 mL d'une solution
de diiode pour percevoir la coloration bleutée persistante.
Dans un second temps, on réalise une dilution au 1/20 de la solution
d'eau de Javel commerciale. On appelle S la solution diluée ainsi
préparée. On prélève 10,0 mL de la solution S à laquelle on ajoute 40,0
mL d'eau, 25,0 mL de la solution d'ion arsénite préalablement dosée,
0,50 g d'hydrogénocarbonate de sodium solide et un peu d'empois
d'amidon. Pour percevoir la coloration bleutée, il a fallu verser VE2
= 8,60 mL d'une solution de diiode.
Préparation des solutions :
1. Pour quelle
raison doit-on ajouter des ions iodure en excès lorsque l'on souhaite
préparer une solution aqueuse de diiode au laboratoire ?
On accroît fortement la solubilité de I 2 dans
l’eau en ajoutant de l’iodure de potassium KI en raison de l’existence
d’un équilibre de complexation : I 2 + I - =
I 3- ; K f =
10 2,9.
Toutes les molécules de diiode passent dans la phase aqueuse sous forme
d'ion I 3-.
2.
Indiquer la méthode (verrerie, précautions à prendre) permettant
d'obtenir 200 mL d'une solution d'eau de Javel diluée au 1/20 de la
solution commerciale.
Port de gant, blouse et lunette.
Prélever 10,0 mL de solution commerciale à l'aide d'une pipette jaugée
+ pipeteur ; placer dans une fiole jaugée de 200 mL contenant 1/3 d'eau
distillée ; compléter jusqu'au trait de jauge avec de l'eau distillée ;
bouger, agiter pour rendre homogène.
C. Propriétés d'une
solution d'ions hydrogénocarbonate.
En solution aqueuse, le dioxyde de carbone dissout CO 2 aq a
des propriétés d'un diacide que l'on notera H 2CO 3
aq appelé
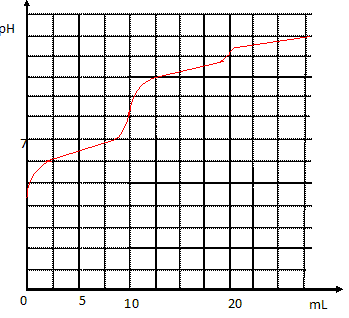
acide carbonique. On dose 10,0 mL d'une solution aqueuse d'acide
carbonique de concentration 0,100 mol/L par une solution de soude de
même concentration. On donne la simulation de la courbe de dosage pH
métrique :
 1.
1. Quelle est
l'équation chimique de la réaction support du titrage pour un volume de
solution de soude versé compris entre 0 et 10 mL. Calculer sa constante
d'équilibre et conclure.
On donne pK a( H 2CO 3 aq /
HCO 3-aq) = 6,4.
H 2CO 3 aq + HO -aq
= HCO 3-aq+ H 2O(l) ; K = [HCO 3-aq]
/ ([H 2CO 3 aq ][HO -aq]
)
K =[HCO3-aq][H3O+aq]
/ ([H2CO3 aq ][HO-aq] [H3O+aq]
) = Ka / 10-14 = 10-6,4 /10-14
=107,6.
Cette valeur est très grande, la réactuion est totale ;
étant de plus rapide, elle peut servir de support à un titrage.
2. Quelle
information nous donne la courbe de dosage en V= 5,0 mL de solution de
soude ajoutée. Justifier.
A la demi équivalence de ce dosage acide faible base forte, les
quantités de matière d'ion HCO3-aq et
de H2CO3 aq sont égales : en
conséquence le pH est égal au pKa du couple acide / base H2CO3
aq / HCO3-aq).
3. Pour quelle
raison n'observe-t-on pas de saut de pH significatif pour un volume
ajouté égal à 20 mL ?
On donne pKa( HCO3-aq /CO32-aq)
= 10,3.
Le pH avant la seconde équivalence est proche de 10,5 ;
le pH de la seconde équivalence sera voisin de 11,5 à 12 ; or en tenant
compte de la concentration de la soude et de la dilution, le pH final
sera proche de 12 : en conséquence un saut de pH important ne peut pas
exister.
4. Justifier que
le pH en V = 10,0 mL correspond à celui d'une solution d'ions
hydrogénocarbonate de concentration 5,00.10-2 mol.L-1.
La réaction support du titrage est totale ; à l'équivalence les
quantités de matière d'ion hydroxyde et d'acide carbonique sont en
proportions stoechiométriques : donc n(HO-aq ajouté
)= n(HCO3-aq) = 10,0 10-3*0,100
= 1,00 10-3 mol dans 20 10-3 L de solution.
[HCO3-aq] =1,00 10-3 /20 10-3
=5,00 10-2 mol/L.
5. Indiquer les 3 propriétés d'une
solution tampon.
Une solution tampon fixe le pH d'une solution a une valeur bien
déterminée.
Une solution tampon modère les variations de pH suite : à l'ajout
modéré d'un acide fort ou d'une base forte, suite à une dilution
modérée.
6. Une solution
aqueuse d’ions hydrogénocarbonate peut-elle être utilisée comme une
solution tampon au laboratoire ? Justifier votre réponse.
Une solution tampon doit contenir les deux espèces d'un couple acide /
base ; les quantités de matière de des deux espèces doivent être
pratiquement identiques pour avoir un pouvoir tampon maximum. Le couple
acide / base (H2CO3 aq / HCO3-aq)
contribue à stabiliser le pH du sang et de nombreux autres liquides
biologiques. Une solution aqueuse d'hydrogénocarbonate de sodium ne
constitue donc pas à elle seule, une solution tampon.
D. Détermination de la
concentration de l'eau de Javel commerciale.
1. Comment
qualifier la méthode proposée du dosage de l'eau de Javel de la
solution S ?
Dosage en retour, ou dosage indirect par différence.
2.
Indiquer les deux demi-équations intervenant dans la réaction
d'oxydo-réduction (1) entre les ions hypochlorite et les ions arsénite.
ClO- aq + 2H+aq + 2e-
= Cl-aq + H2O(l)
AsO2- aq + 2H2O(l) = AsO43-
aq+ 4H+aq +2e- .
Bilan : ClO- aq +AsO2-
aq +H2O(l) = Cl-aq
+ 2H+aq +AsO43- aq
(1).
3. Ecrire les
formules de Nernst relatives aux couples AsO43- aq
/AsO2- aq et ClO- aq / Cl-aq.
E1 = E°( ClO- aq / Cl-aq)
+0,03 log([ClO- ][H+]2 / [ Cl-
] )
E1 =1,72 +0,03 log([ClO- ][H+]2
/ [ Cl- ] )
E2 = E°(AsO43- aq /AsO2-)
+0,03 log([AsO43- ][H+]4 /
[AsO2- ] )
E2 = 0,98 +0,03 log([AsO43- ][H+]4
/ [AsO2- ] ).
4. Calculer la
constante d'équilibre de la réaction (1).
K =[AsO43- ][H+]2[ Cl-
] /([AsO2- ][ClO- ])
A l'équilibre E1 = E2 : 1,72 +0,03 log([ClO-
][H+]2 / [ Cl- ] ) =0,98 +0,03 log([AsO43-
][H+]4 / [AsO2- ] )
1,72-0,98 = 0,03 log K ; log K = 24,67 ; K =
4,6 1024.
5. Calculer la
concentration exacte C1 en ion arsénite.
A l'équivalence la quantité de matière de diiode est
égale à celle d'ion arsénite d'après (2) : C2VE1
= V1 C1.
C1 = C2VE1 / V1 =5,00 10-2*9,6
/ 10,0 =4,8 10-2 mol /L.
6. Calculer la concentration C3
en ion hypochlorite dans la solution S.
Quantité de matière initiale en ion arsénite : 25,0 10-3 *
4,8 10-2 =1,20 10-3 mol
Quantité de matière d'ion arsénite en excès : C2VE2=5,00
10-2*8,6 10-3 =4,3 10-4 mol
Quantité de matière d'ion arsénite ayant réagi avec l'ion hypochlorite
: =1,20 10-3 -4,3 10-4 =7,7 10-4 mol.
D'après (1) : [ClO-]= 7,7 10-4 /0,010 =7,7 10-2 mol/L.
Tenir compte de la dilution : 7,7 10-2 * 20 = 1,54 mol/L.
7. Retrouver le pourcentage en chlore actif dans la
solution d'eau de Javel commerciale.
Cl2(g) + 2HO-aq --> ClO-
aq + Cl- aq +H2O(l).
n(Cl2) = n(ClO-) = 1,54 mol dans 1 L soit 1,54 *
71 = 109,3 g de dichlore dans 1 L ( c'est à dire dans 1158 g de
solution).
109,3 / 1158*100 = 9,4 % ( écart avec l'indication ~ 2%).
Analyse, caractérisation.
A. Voici la formule
d’un composé organique :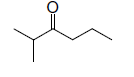
1. Donner le nom de
cette molécule ainsi que sa fonction.
Cétone : 2 méthylhexan-3-one.
2. Lequel de ces
deux spectres 1H correspond à la molécule. Justifier votre réponse :
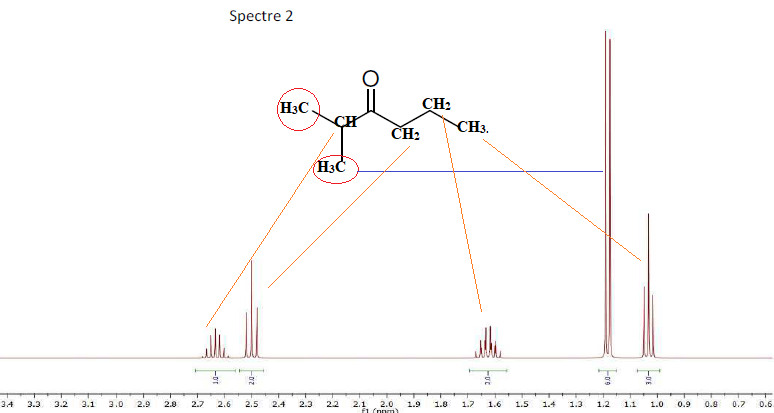
B. On réalise au
laboratoire une synthèse organique et on veut vérifier par
chromatographie sur couche mince la pureté du produit.
1. Expliquer
brièvement le principe de la CCM.
2. Donner les 4
étapes de la réalisation de ce chromatogramme.
But : séparer et identifier les
constituants d'un mélange.
Mise en
oeuvre : placer
l'éluant dans le bécher ( hauteur 5 mm), mettre un couvercle.
Sur la plaque CCM, tracer 2 traits au crayon de papier à 7 ou 8 mm des
extrémités.
Sur le trait inférieur faire les dépots (pipette pasteur), espèces à
analyser et substances étalon.
Placer la plaque dans le bécher, fermer, retirer dés que l'éluant
atteint le trait supérieur.
Nomenclature.
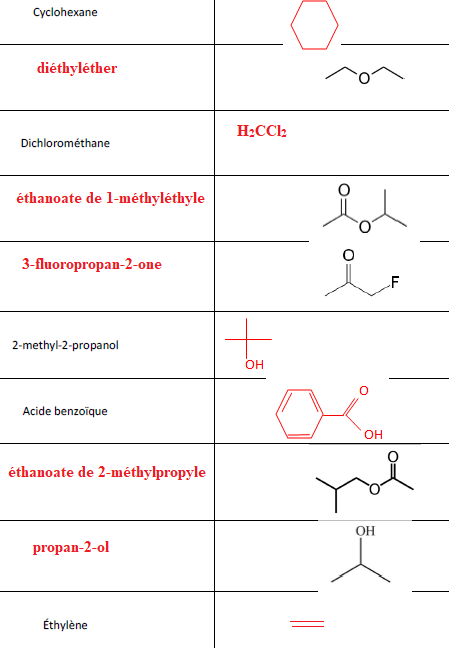
|
...
|
....
|
Analyse de la fiche toxicologique du
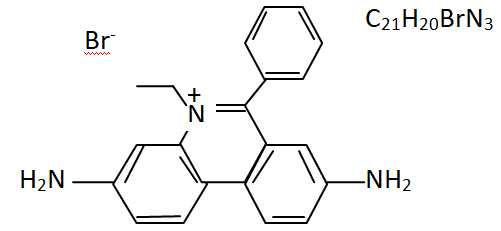
Bromure d’Ethidium.
1. Donner la
formule brute du BET (Bromure d’EThidium).
2. Noter le numéro
CAS du produit et expliquer son utilité
1239-45-8. Ce numéro identifie une espèce chimique sans aucune
ambiguité.
3. Quels sont les
dangers de ce produit ? Donner la signification des pictogrammes de
sécurité ?
4. Quels sont les
risques pour la santé ?
Susceptible d'induire des maladies génétiques ; mortel par
inhalation ; nocif en cas d'ingestion.
5. Quelles sont les
précautions à avoir lors de son utilisation ? Et lors de son stockage ?
Manipulation sous hotte chimique.
l'utilisateur doit porter un sarrau fermé, des chaussures fermées, des
gants résistants aux produits chimiques et des lunettes de sécurité.
Se laver les mains après avoir retiré les gants.
Syockage dans des locaux séparés, bien ventilés aménagés pour des
produits génotoxiques, balisés par une signalisation.
6. Que doit-on
faire après avoir renversé un flacon contenant une solution de BET et
avoir mis le coude dans le liquide ?
Laver la région affectée avec du savon et de l'eau froide, rincer
abondamment.
Optique.
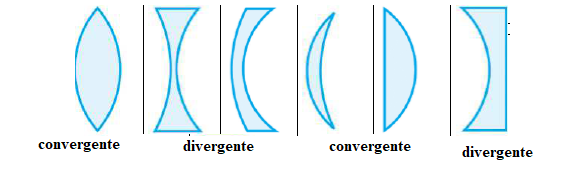
1. Pour chacune des
lentilles schématisées ci-dessous, dire si elle est convergente ou
divergente.
2. Proposer une
méthode simple pour déterminer la distance focale d’une lentille
convergente et la représenter par un schéma.
L'image
donné par une lentille convergente d'un objet situé à l'infini, se
trouve dans le plan focal image de la lentille.
- former l'image nette d'un objet lointain, assez lumineux (immeuble
éclairé par le soleil, lampe éloignée...) sur un écran. .
- mesurer la distance lentille écran : elle donne une bonne
approximation de la distance focale de la lentille.
3. Un microscope optique peut être
modélisé par deux lentilles minces coaxiales convergentes, l’objectif
et l’oculaire.
Soit L1 l’objectif, de centre optique O1 et de
distance focale f1’ = 8 mm. Soit L2 l’oculaire,
de centre optique O2 et de distance focale f2’ =
20 mm. On appellera F1 et F2 les foyers objets
des lentilles, respectivement pour l’objectif et l’oculaire, et F1’
et F2’ les foyers images, respectivement l’objectif et
l’oculaire. L’intervalle optique est défini par la distance entre F1’
et F2 et vaut Δ = 160 mm.
On place un objet réel AB, perpendiculaire à l’axe optique tel que le
point A soit situé sur l’axe et en avant de l’objectif.
On règle le microscope de manière à donner une image à l’infini et on
observe cette image avec un oeil emmétrope (oeil normal adulte) placé
en arrière du foyer image F2’ de l’oculaire. On rappelle que
l’oeil émmetrope nu peut voir nettement les objets situés entre δ = 25
cm (punctum proximum) et l’infini (punctum remotum).
a) L’oeil a-t-il
besoin d’accommoder ? Justifier.
L'image définitive se trouvant à l'infini, l'oeil observe sans fatigue,
sans accommoder.
b) Représenter
schématiquement le microscope et l’objet AB, sans respecter l’échelle.
Représenter la trajectoire de deux rayons lumineux issus de B, l’un
émis parallèlement à l’axe optique, l’autre passant par F1.
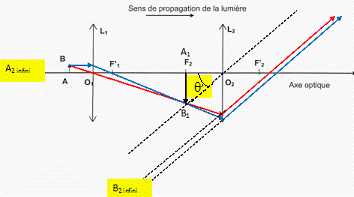
c) Calculer la distance séparant les
deux lentilles.
O1F'1 + D
+F2O2 =8 +160 +20 =188 mm.
d) Calculer la
distance AO1 pour un objectif de grandissement x20.
Commenter.
20 = O1A1 / AO1 ; AO1 = 168
/ 20 =8,4 mm, objet de petites dimensions.
e) Calculer le
grossissement de l’oculaire G2 donné par l’expression G2=punctum
proximum / f2’.
G2 = 250 /20 =12,5.
f) Calculer GM
le grossissement du microscope.
GM = 20 G2 =250.
Thermodynamique.
Le service projette l’acquisition d’une chromatographie gazeuse couplée
à un spectromètre de masse.
Le gaz vecteur sera l’hélium, son débit optimal en fonctionnement sera
d’après le constructeur de 20 mL.min-1 à la pression de
76000 Pa et 25°C.
L’appareil sera en fonctionnement 24/24 toute l’année.
Le fournisseur de gaz propose 3 types de conditionnement.
Données : Pour la pression atmosphérique on prendra 1 105 Pa
ou 1 bar ; He : 4 g.mol-1 ; densité 0,14 ; masse volumique
0,169 kg.m-3.
1. Donner le
volume
de gaz disponible dans les conditions de fonctionnement de l’appareil
pour chaque conditionnement. Détailler vos calculs..
type
|
Volume
contenant
|
pression
|
volume
gaz disponible
|
autonomie
|
emballage
|
litres
|
à
25°C en bar
|
en
m3
|
en
jours
|
M50
|
50
|
200
|
13
|
456
|
M20
|
20
|
200
|
5,3
|
183
|
S11
|
11
|
200
|
2,9
|
101
|
A
température et quantité de matière consatntes, V =0,050 x200 /
0,76 =13,15 ~13 m3.
Autonomie : 13,15 106 / 20 =6,575 105 min =1,095
104 heures ~456 jours.
3. En sachant que
chaque rechargement induit un coût supplémentaire et que quel que soit
le conditionnement le coût de la location à l’année et le prix du m3
sont identiques ; quel serait votre choix de conditionnement ?
Détailler votre calcul.
type
|
Volume
disponible
à 1 atm et 25°C
en m3( Vd)
|
prix
du litre (PI)
|
prix
bouteille(PB)
|
prix
chargement
bouteille (Pcb)
|
nombre
bouteille par an (N) |
coût
par an |
M50
|
10
|
0,1
|
75
|
100
|
1
|
1175
|
M20
|
4
|
0,1
|
50
|
100
|
2
|
1075
|
S11
|
2,2
|
0,1
|
30
|
100
|
4
|
1310
|
Coût
=1000 Vd x PI +PB +N x PcB, la bouteille étant achetée une seule fois.
M50 : une bouteille par an ; 1000 x10 x0,1+75 +100 =1175 €.
M20 : 2 bouteilles par an ; 8000 x10 x0,1+50 +2 x100 =1050 €.
M50 : 4 bouteilles par an ; 8800 x10 x0,1+30 +4 x100 =1310 €.
Viscosité.
Nous devons réaliser des essais mécaniques dans une cuve d’huile de
Jatropha Curcas. Afin d’optimiser les essais, nous
devons connaitre la viscosité de l’huile.
Pour cela nous disposons d’un viscosimètre à bille thermo régulé à 20°C
et d’une bille d’acier inox de diamètre 11,5 mm.
La viscosité est donnée par la relation suivante :
h =KR2gt
( rbille-rhuile) cos a.
Où : η = viscosité en Pa.s
K = constante du viscosimètre en m-1
R = rayon de la bille en m
g = intensité de pesanteur en m.s-2
t = temps en s
ρ = masse volumique en kg.m-3
α = angle en radian par rapport à la verticale
L’eau ultra pure (UHQ) est utilisée pour déterminer la constante de
calcul K, propre à notre viscosimètre.
Afin de déterminer la masse volumique de l’huile, nous disposons d’un
pycnomètre de 10 mL et son thermomètre, gradué à 0,2°C, qui ont été
étalonnés par le constructeur en 2014. La balance de model A120S de
chez Satorius, d’une précision de 0,1mg a été vérifiée le 07 janvier
2018 en interne au laboratoire. La masse volumique est obtenue à partir
de la pesée d’un pycnomètre sec à température ambiante.
Calculez, à partir des données, la masse volumique et la viscosité de
l’huile de Jatropha Curcas utilisée.
Données :
Volume du pycnomètre : 9,964 mL
Température de l’huile : 19,8 °C
Température du viscosimètre : 20,1 °C
Masse du pycnomètre vide : 29,9571 g
Masse du pycnomètre avec l’huile : 39,0591 g
Angle d’inclinaison du viscosimètre : 0 °
Masse volumique de la bille : 7826,81 Kg.m-3
Masse volumique de l’eau UHQ : 1000 g.L-1
Intensité de la pesanteur : 9,81 m.s-2
Temps de chute la bille dans l’huile : 67,78 s
Temps de chute de la bille dans l’eau : 2,4 s
Viscosité de l’eau à 20 °C : 1,002.10-3 Pa.s.
Masse volumique de l'huile :(39,0591-29,9571) / 9,964=0,9135 g / mL = 913,5 Kg.m-3.
heau =KR2gteau
( rbille-reau) cos a.
hhuile =KR2gthuile
( rbille-rhuile) cos a.
hhuile / heau =thuile
/ teau( rbille-rhuile) / ( rbille-reau).
hhuile / heau =67,78 / 2,4 x(7826,81 -913,5) / (7826,81 -1000)=28,24 x 6913,31 /6826,51 = 28,6.
hhuile =28,6 x1,002.10-3 = 2,865 10-2 Pa.s.
|
|






