Physique,
concours avenir 2021.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
.
.
|
..
..
......
...
|
Une
seule réponse exacte par question. Chque réponse exacte est gratifiée
de 3 points ; chaque réponse fausse est pénalisée par le retrait d'un
point.
Durée : 1 h ;
coefficient 4.
Jupiter est une planète géante gazeuse. Il s'agit de la plus grosse
planète du Système solaire, plus volumineuse et massive que toutes les
autres planètes réunies, et la cinquième planète par sa distance au
Soleil (après Mercure, Vénus, la Terre et Mars).
Comme sur les autres planètes gazeuses, des vents violents, de près de
600 𝑘𝑚.ℎ−1,
parcourent les couches supérieures de la planète. La Grande Tache rouge
(noté GTr) est un anticyclone, une zone de surpression observée depuis
au moins le 𝑋𝑉𝐼𝐼𝑒 siècle. Trois fois plus grande que la Terre au
début du 𝑋𝑋𝑒 siècle, elle a rétréci pour devenir de taille
comparable un siècle plus tard.
La Grande Tache rouge est un gigantesque anticyclone de l'atmosphère de
Jupiter situé à 22° sud de latitude. Longue d'environ 15 000 kilomètres
et large de près de 12 000 kilomètres (informations de 2015).
Une sonde AVENIR21 a été envoyée afin d'examiner de plus près cette
Grande Tache rouge (GTr) et de récolter des données pour en connaitre
ses caractéristiques. Ce sujet traite de la mise en orbite de cette
sonde AVENIR21 et de quelques mesures effectuées.
Exercice n°1 :
La sonde AVENIR21 est en orbite jovienne-stationnaire autour de Jupiter
avec une période de 𝑇𝐽=10ℎ. Elle est caractérisée
par un mouvement circulaire et uniforme dans le référentiel
jovicentrique.
Données : - Intensité du champ de pesanteur de Jupiter à une distance 𝑅𝐽
de son centre de masse : 𝑔=25 𝑚.𝑠−2
- Rayon de Jupier : 𝑅𝐽=70 000 𝑘𝑚
- Rayon de l'orbite jovienne-stationnaire : 𝑟=90 000 𝑘𝑚
- Vitesse de la sonde sur son orbite : 𝑣=30 𝑘𝑚.𝑠−1
- Constante de gravitation universelle : 𝐺≈10−10 𝑈𝑆𝐼
1. L'unité de la
constante de gravitation universelle s'exprime en :
a. 𝑁.𝑚2.𝑘𝑔−1
b. 𝑁.𝑚2.𝑘𝑔−2
vrai
c. 𝑁.𝑚.𝑘𝑔−2
d. 𝑁.𝑚.𝑘𝑔−1.
F = G M m / d2 ; G = Fd2 /(Mm).
G s'exprime en N m2 kg-2
soit kg m s-2 m2
kg-2 soit m3 kg-1 s-2
2.
L'expression de l’intensité du champ de pesanteur de Jupiter, dont la
valeur figure dans les données, est :
a. g =GMJ
/ RJ2. Vrai.
b. g= -GMJ
/ RJ2.
c. g =GMJ
/ RJ.
d. g = -GMJ
/ RJ.
3.
La masse de Jupiter est de l'ordre de :
a. 1,23×1021
kg
b. 1,23×1024
kg
c. 1,23×1027
kg vrai
d. 1,23×1030
kg.
g = GMJ / RJ2 ;
MJ =gRJ2
/ G = 25 x(7 107)2 / (10-10)=1225
x1024 ~1,3 1027 kg.
4. 4.
L'expression de la valeur de la vitesse de la sonde AVENIR21 sur son
orbite autour de Jupiter en fonction du rayon r est :
a. 2p (GMJ / r)½.
b. 2p (GMJ / r2)½.
c. (GMJ / r2)½.
d. (GMJ
/ r)½. Vrai.
Accélération a = v2 / r = GMJ
/ r2 ; v2 = GMJ
/ r.
5. L’expression de
r en fonction de la période jovienne-stationnaire TJ est :
a. [GMJTJ
/ (4p2)]1/3.
b. [GMJTJ2
/ (4p2)]1/3.
Vrai.
c. [GMJTJ
/ (2p)]1/3.
d. [GMJTJ2
/ (2p)]1/3.
La sonde décrit la circonférence 2 p r à la vitesse v pendant
la durée TJ.
2 p r =vTJ ; 4p2r2 = v2 TJ2= GMJ / r TJ2
;
4p2r3 =GMJ TJ2
; r3 =GMJ TJ2
/ (4p2).
6. Le
vecteur accélération de la sonde AVENIR21 sur son orbite est :
a. Centripète vrai
b. Tangente à la trajectoire
c. Nulle
d. Constante.
7. La valeur de
l’accélération de la sonde sur son orbite est :
a. 0,33 m s-2.
b. 3 m s-2.
c. 10 m s-2.
Vrai.
d. 1000
m s-2.
a = v2 / r =(3 104)2
/ (9 107) = 90 / 9 = 10 m s-2.
Exercice n°2 :
La sonde AVENIR21 est équipée d’un capteur couplé à
une lunette
astronomique, système afocal, permettant de prendre des images de
Jupiter et de la GTr.
Caractéristiques de la lunette :
- Vergence de l'objectif : C1 = 0,5 d.
- Vergence de l'oculaire : C2 = 5 d.
8.
Si un faisceau de lumière provenant d’un objet à l’infini arrive
parallèlement à l’axe optique de la lunette, alors le faisceau sortira
de la lunette :
a. Parallèle à
l’axe optique. Vrai.
b. Incliné d'un
angle 𝛼 par rapport à l’axe optique
c. Incliné d'un
angle −𝛼 par rapport à l’axe optique
d. Incliné d'un
angle 2𝛼 par rapport à l’axe optique.
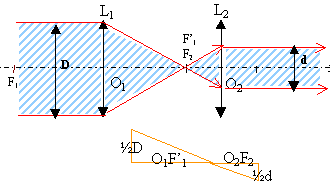 9.
9. La distance
entre l’objectif et l’oculaire est :
a. 1,8 m
b. 2,0 m
c. 2,2 m vrai.
d. 5,5 m.
O 1F 2+F 2O 2 =1 /C 1
+1/C 2 =1 /0,5 +1 /5 = 2,2 m.
10. L'image donnée
par l’objectif, d’un objet à l’infini, se trouve :
a. Sur le plan
focal image de l'objectif vrai
b. Après le foyer
objet de l'oculaire
c. Avant le foyer
objet de l'oculaire
d. Sur le plan
focal image de l'oculaire.
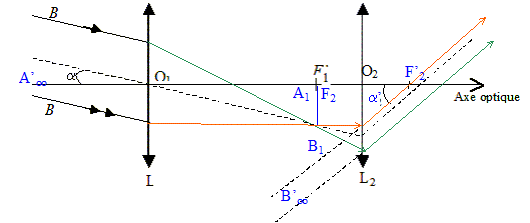
11. Le
grossissement de cette lunette est :
a. G = 0,1 ; b.
G =5 ; c. G =10 vrai ; d. G =20.
tan a' = a' (rad) =
A 1B 1 / O 2F' 2 ;
tana =a (rad) = A1B1
/ O1F'1 ;
La valeur du grossissement G de cette
lunette vaut G= a'/ a=O1F'1
/ O 2F' 2=2 / 0,2 = 10 .
12.
Entre la lunette et le capteur, un filtre ne laissant passer que les
radiations rouges est appliqué. Les ondes arrivant au capteur ont alors
une fréquence comprise entre :
a. f=6,0× 1014 Hz et 7,5×1014
Hz
b. f=3,7× 1014
Hz et 5,0×1014 Hz. Vrai.
c. f=7,5× 1014
Hz et 1,3×1015 Hz
d. f=3,7× 1015
Hz et 6,0×1015 Hz.
Longueur d'onde des radiations rouges l ~7 10-7 m.
Fréquence : 3 108 / (7 10-7) ~4 1014
Hz.
13. Ces radiations
rouges passent après le filtre par une fente rectangulaire de largueur
a = 400 µm . L’écart angulaire de diffraction 𝜽 pour chaque radiation
ayant traversé la fente est :
a. Supérieur à
0,0015 rad. Vrai.
b. Inférieur à
0,0015 rad
c. Compris entre
0,0010 rad et 0,0015 rad
d. Compris entre
0,0008 rad et 0,0010 rad.
q = l /a =7 10-7 / 4
10-4 ~1,8 10-3 rad =0,0018 rad.
.
14. Si la fente
rectangulaire est remplacée par une double fente alors une figure
d’interférence sera observée sur le capteur. Deux ondes cohérentes
interféreront de façon destructive sur le capteur, si leur différence
de chemin optique est égale à :
a. 𝛿=(2𝑘+1)𝜆 𝑎𝑣𝑒𝑐
𝑘 𝑢𝑛 𝑛𝑜𝑚𝑏𝑟𝑒 𝑒𝑛𝑡𝑖𝑒𝑟 𝑟𝑒𝑙𝑎𝑡𝑖𝑓
b. 𝛿=(2𝑘+1)𝜆 /2
𝑎𝑣𝑒𝑐 𝑘 𝑢𝑛 𝑛𝑜𝑚𝑏𝑟𝑒 𝑒𝑛𝑡𝑖𝑒𝑟 𝑟𝑒𝑙𝑎𝑡𝑖𝑓 vrai
c. 𝛿=(𝑘+1)𝜆
𝑎𝑣𝑒𝑐 𝑘 𝑢𝑛 𝑛𝑜𝑚𝑏𝑟𝑒 𝑒𝑛𝑡𝑖𝑒𝑟 𝑟𝑒𝑙𝑎𝑡𝑖𝑓
d. 𝛿=(𝑘+1)𝜆/2
𝑎𝑣𝑒𝑐 𝑘 𝑢𝑛 𝑛𝑜𝑚𝑏𝑟𝑒 𝑒𝑛𝑡𝑖𝑒𝑟 𝑟𝑒𝑙𝑎𝑡𝑖𝑓.
|
...
|
....
|
Exercice n°3 :
La Grande Tache rouge (GTr) de Jupiter a été à de nombreuses reprises
observée par des sondes. La sonde AVENIR21 a mesuré les dimensions de
cet anticyclone de forme quasi cylindrique de diamètre d et de hauteur
h. Des relevés infrarouges ont également permis de mesurer la
température à l’extérieur de la Tache et dans la Tache.
Données : - Diamètre de la GTr : d=16 000 km
- Hauteur de la GTr : h=10 000 km
- Température à l’extérieur de la GTr : Tb=160
°𝐶
- Température de la GTr : Tc=10 °𝐶
- Capacité thermique de la GTr 𝐶𝑃=4 kJ kg-1
K-1.
- Quantité de matière de gaz contenue dans la GTr : n
- Constante des gaz parfaits : R
- Masse volumique du gaz contenue dans la GTr : r=1500 𝑘𝑔.𝑚−3
- On considère que la pression et la température du gaz dans la GTr
sont uniformes.
- On considère le gaz dans la GTr comme incompressible et parfait.
- La GTr est un système fermé.
15. Le facteur de
proportionnalité entre la pression et la température du gaz dans la GTr
est :
a. k
= n / (RV).
b. k =-RV / n.
c. k = nR / V. Vrai.
d. k = RV / n.
PV = nRT ; P = nR / V T = k T.
16. La masse de gaz contenu dans la
GTr est approximativement :
a. 3 1019
kg ; b. 3 1021
kg ; c. 3 1022 kg ; d. 3 1024 kg. Vrai
Volume du
cylindre V = pd2
/ 4 h =3,14 x(1,6 107)2 / 4 x107 ~2 1021
m3.
Masse = volume fois masse volumique = 2 1021 x1500 ~3 1024
kg.
17. La variation
d’énergie interne du gaz contenu dans la GTr, si sa température passe
de 𝟏𝟎 ° à 𝟏𝟏𝟎 ° , est :
a. Δ𝑈=1,2 1030
𝐽 Vrai
b. Δ𝑈=2,0 1028
𝐽
c. Δ𝑈=1,2 1027
𝐽
d. Δ𝑈=1,5 1027
𝐽.
m Cp DT =3 1024 x 4
x100 =1,2 1027 kJ.
18. Le
flux thermique entre l’extérieur et l’intérieur de la GTr est :
a. Inversement
proportionnel à la différence de température entre l’extérieur et
l’intérieur de la GTr
b. Proportionnel à
la différence de température entre l’extérieur et l’intérieur de la
GTr. Vrai .
c. Indépendant de
la différence de température entre l’extérieur et l’intérieur de la GTr
d. Proportionnel au
carré de la différence de température entre l’extérieur et l’intérieur
de la GTr
19. Les échanges
thermiques au sein de la GTr se font majoritairement par :
a. Rayonnement
b. Conduction.
c. Convection. Vrai.
d. Les trois propositions
précédentes.
La température 𝑇(𝑡) de la GTr en contact avec
l’extérieur, thermostat de température constante 𝑇𝑒𝑥𝑡 ,
vérifie l’équation différentielle suivante :
𝑑𝑇(𝑡) / 𝑑𝑡+𝑘.𝑇(𝑡)=𝑘.𝑇𝑒𝑥𝑡
avec 𝑘 une constante positive.
20. La dimension de
1 /k est homogène à :
a. Une durée. Vrai.
b. Une
température.
c. Une
longueur d’onde
d. Une conductivité
thermique.
21. La solution
d’une telle équation différentielle d’ordre 1 est du type :
a. 𝑇(𝑡)=𝐴𝑒𝑘𝑡
+𝐵 avec 𝐴 et 𝐵 des constantes
b. 𝑇(𝑡)=𝐴𝑒-𝑘𝑡
+𝐵 avec 𝐴 et 𝐵 des
constantes. Vrai.
c. 𝑇(𝑡)=𝐴𝑒𝑘𝑡
avec 𝐴 une constante
d. 𝑇(𝑡)=𝐴𝑒-𝑘𝑡
avec 𝐴 une constante.
Exercice n°4 :
La sonde AVENIR21 analyse aussi des particules. Des
particules captées par la sonde, entrent dans un condensateur plan en O
et avec une vitesse v0 suivant
l’axe Ox. La sonde détermine, pour
chaque particule, l’altitude YS
et l’instant ts de sortie du
condensateur. Cette expérience permet de connaitre le rapport charge
sur masse pour une particule. On négligera les forces d’attractions
gravitationnelles subies par la particule. Le condensateur plan utilisé
est représenté par la figure ci-dessous :
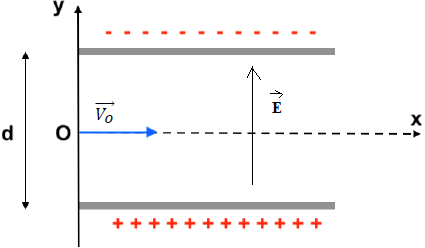
A 𝑡=0 𝑠, une particule inconnue de charge q et de masse m entre en O
avec une vitesse v0 dans le
condensateur plan, zone où règne un champ électrostatique. Les plaques
du condensateur sont séparées par du vide.
Données : - Permittivité du vide : 𝜀0= 10−11
𝐹.𝑚−1
- Valeur du champ électrostatique régnant entre les plaques : 𝐸=100
𝑉.𝑚−1
- Distance entre les plaques : 𝑑=10 𝑐𝑚
- Surface d’une plaque du condensateur : 𝑆=50 𝑐𝑚2
- Charge élémentaire : 𝑒=10−19𝐶
- Longueur des plaques : L
- Formule permettant de calculer la capacité C d’un condensateur plan
dont les plaques de surface S sont séparés, par du vide, d’une distance
d : C = 𝜀0.𝑆 / 𝑑.
22. La valeur de
la différence de potentiel U entre les plaques vaut :
U = 1000 V ; U = 100 V ; U = 10 V vrai
; V = 1 V.
U = E d = 100x0,10 = 10 V.
23. Les coordonnées de
l’accélération de la particule de charge q, dans le repère cartésien
(O,x,y), sont :
a. ax =0
; ay = qE .
b. ax =0 ; ay
= -qE
c. ax =0 ; ay
= q / m E. Vrai.
c. ax =0 ; ay
= -q / m E.
La particule n'est soumise qu'à la froce électrostatique F = qE. La
seconde loi de Newton conduit à :
ax = 0 et may = qE soit ay = qE / m.
24. Les coordonnées de la
position de la particule dans le condensateur sont :
a. x(t) = v0t
; y(t) = -q/m Et2 ;
b. x(t) = v0t ; y(t) =
0,5q/m Et2 ; vrai.
c. x(t) = 0 ; y(t) = -0,5q/m Et2
+v0t ;
d. x(t) = 0 ; y(t) = -q/m Et2
+v0t.
Le vecteur vitesse est une primitive du vecteur accélération.
vx = Cste = v0 ; vy = q / m Et.
Le vecteur position est une primitive du vecteur vitesse.
x = v0 t ; y = 0,5q/m
Et2 la position initiale étant l'origine du repère.
25. La particule sort du
condensateur avec pour ordonnée yS = -4 cm et à
l'instant tS = 32 ms. On en déduit que le rapport q / m vaut
:
a. − 8 .10−5
C kg-1.
b. + 8
.10−3 C kg-1.
c. − 8 .10−1
C kg-1. Vrai.
d. − 8
.101 C kg-1.
q / m = 2yS / (ETS2) =-0,08 /
(100*0,0322) =
− 8 .10−1
C kg-1.
26. La capacité du condensateur est
:
a. C = 5 10-10
F.
b. C = 5 10-12 F.
c. C = 5 10-13 F.
Vrai.
d. C = 5 10-14 F.
C = 𝜀0.𝑆
/ 𝑑 = 10-11 x50 10-4 /0,10 =5
10-13 F.
27. La valeur absolue de
la charge totale présente sur une plaque du condensateur vaut alors :
a. |𝑄|=5 .10−12
𝐶 vrai; b. |𝑄|=5 .10−11 𝐶 ; c. |𝑄|=2 .10−11 𝐶 ; d. |𝑄|=2 .10+13 𝐶.
|Q| = C U = 5 10-13 x10 = 5 10-12 C.
28. Un condensateur
lorsqu’il se décharge :
a. Libère de
l’énergie. Vrai.
b. Absorbe de
l’énergie
c. Voit la tension
à ses bornes augmenter
d. Stocke de
l’énergie électrique.
29. Le temps de
décharge d’un condensateur en série avec une résistance R :
a. Est
proportionnel à la tension initiale aux bornes du condensateur.
b. Est proportionnel à la
résistance R du circuit et à la capacité C du condensateur. Vrai. (t ~ 5 RC)
c. Est inversement
proportionnel à la résistance R du circuit et à la capacité C du
condensateur.
d. Est inversement
proportionnel à la tension initiale aux bornes du condensateur.
30. Le courant
traversant un condensateur, dont la tension à ses bornes est Uc ,
s’exprime :
a. i(t) =dUc/dt.
b. i(t) =1 / C dUc/dt.
c. i(t) =R / C dUc/dt.
d. i(t) =C dUc/dt. Vrai.
i = dQ /dt = d(CUc)/dt
= C dUc/dt.
Questions bonus.
NUMERIQUE
1. Quel est le
résultat de cette requête SQL
SELECT nom FROM etudiant;
a. Elle affiche
tous les noms d’une table etudiant.
Vrai.
b. Elle affiche tous les champs
d’une table etudiant
c. Elle affiche
certains noms d’une table etudiant.
d.Elle affiche tous les noms d’une
table etudiant triés par ordre alphabétique.
2. Quel est le résultat de
l’exécution du code Python suivant
liste[7, 3, 6, 4, 5, 2, 8, 1]
print ([i % 2 for i in liste])
a. [0, 0, 1, 1, 0,
1, 1, 0]
b. [1, 1, 0, 0, 1,
0, 0, 1] vrai
c. [3, 1, 3, 2, 2,
1, 4, 0]
d. Une erreur.
On écrit zéro pour un nombre pair et 1 pour un nombre impair.
3. La mémoire dans
un ordinateur est organisée en blocs de quelle taille ?
a. 4 bits
b. 8 bits vrai.
c. 4 octets
d. 32 bits.
Sciences de l'ingénieur.
4. La résistance
équivalente de ce circuit est :
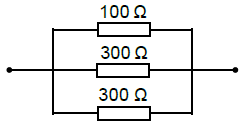
1 / Réq=1 /100 +1 /300 +1/300 = 3 /300+1/300+1/300 = 5 /300.
Réq = 300 / 5 = 60 ohms. Réponse
b.
5. On donne : E = 12 V ; R1
= 1 kΩ et R2 = 2 kΩ. La valeur de la tension U est :
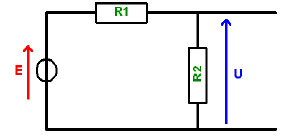
u = ER2 /(R1+R2) = 12*2 /3=8 V.
Réponse c.
6. Le nombre 92 en
hexadécimal s’écrit en binaire :
a. 1001 0010
b. 1001 0011
c. 1000 0010
d. 0111 1110.
Réponse a.
SVT.
7. Où se déroule
la photosynthèse ?
a. Dans le noyau
des cellules végétales.
b. Dans les
mitochondries des cellules végétales.
c. Dans les
chloroplastes des cellules végétales. Vrai.
d. Dans le
cytoplasme des cellules végétales.
8. Quelle est la
valeur normale de glycémie ?
a. 0,7 g/L.
b. 1 g/L.Vrai.
c. 1,5 g/L.
d. 2 g/L.
9. Où la
lithosphère océanique est-elle produite ?
a. Au niveau des
zones de subduction.
b. Au niveau des
zones de rifting.
c. Au niveau des
zones de collision.
d. Au niveau des
zones de dorsales. Vrai.
PHYSIQUE :
1. Une onde
progressive :
a. Transporte de
l’énergie.Vrai.
b. Transporte de la
matière.
c. Transporte
de l’énergie et de la matière.
d. Ne transporte ni
énergie ni matière.
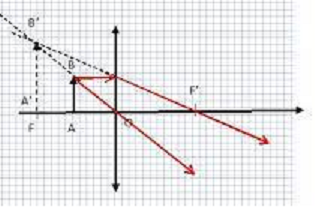
2. L’image virtuelle d’un
objet obtenue à travers une lentille mince convergente est :
a. Plus petite que
l’objet
b. Plus grande que
l’objet. Vrai.
c. Renversée par rapport
à l’objet
d. Cela dépend.
3. Soit A et B deux
points d’un fluide de masse volumique 𝜌. Dans un repère (O,x,y,z),
avec l’axe z vertical et orienté vers le haut, la relation entre la
pression 𝑷𝑨 au point A d’altitude 𝒛𝑨 et la pression 𝑷𝑩 au point B
d’altitude 𝒛𝑩 s’écrit :
a.
𝑃𝐵−𝑃𝐴=𝑚𝑔(𝑧𝐴−𝑧𝐵)
b.
𝑃𝐵−𝑃𝐴=𝑚𝑔(𝑧𝐵−𝑧𝐴)
c.
𝑃𝐵−𝑃𝐴=𝜌𝑔(𝑧𝐴−𝑧𝐵) vrai
d.
𝑃𝐵−𝑃𝐴=𝜌𝑔(𝑧𝐵−𝑧𝐴)
|
|
|
|