Géométrie dans l'espace.
Question 1.
On suppose l’espace muni d’un repère orthonormé.On
définit les points A,B et C comme étant les points de coordonnées
respectives (8 ;−2 ;4), (8 ;−2 ;14) et (0 ;−2 ;−2). On a alors :
a. AB > AC
b. AB = AC vrai
c. AB < AC
d. on ne peut pas comparer AB et AC.
AB = [(8-8)
2 +(-2-(-2))
2 +(14-4)
2]
½ = 10.
AC = [(0-8)2 +(-2-(-2))2 +(-2-4)2]½ = 10.
Question 2.
On suppose l’espace muni d’un repère orthonormé.
Soient P le plan d’équation cartésienne 2x −3y +6z −2 = 0 et A le
point de coordonnées (−1 ;−1 ;−1). La distance du point A au plan P est
égale à :
a. 1 vrai ; b. 2 ; c. 3 ; d. 7.
Soit K le projeté orthogonal du point A sur le plan P :
Equation paramétrique de la droite (AK) de vecteur directeur (2 ; -3 ; 6) :
x = 2t-1 ; y = -3t-1 ; z = 6t-1 avec t réel.
K appartient au plan (P) :
2xK −3yK +6zK −2 = 0.
2(2t-1) -3(-3t-1)+6(6t-1)-2 = 0 , 49 t = 3 ; t = 7 / 49 = 1 /7.
K( 2 / 7 -1 ; -3 /7 -1 ; 6 / 7-1) soit ( -5 /7 ; -10 /7 ; -1 /7).
AK = [(xK+1)2 +(yK+1)2 +(zK+1)2]½ = [(2 / 7)2+(-3 / 7)2+(6 / 7)2]½ .
AK = [49 /49]½=1.
Question 3.
Parmi les égalités suivantes, laquelle est vraie quels que soient les vecteurs u et v ?

Question 4.
On suppose le planmuni d’un repère orthonormé d'origine O.
C désigne le cercle de centre O et de rayon 1.
Soit ABCD un carré dont les sommets appartiennent à C et dont chaque côté est parallèle à l’un des axes du repère.
Quelle est la longueur d’un côté de ce carré ?
a. 1 ; b. 2½ vrai ; c. 3½ ; d. 2 / 3.
Equation du cercle : x2 +y2 = 1.
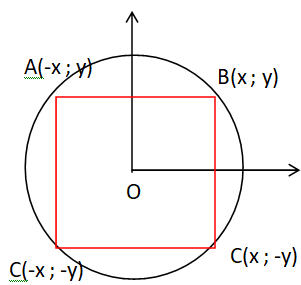
AB = [(x+x)2 +(y-y)2 ]½=2x.
BC = [(x-x)2 +(-y-y)2 ]½=2y.
AB = BC : x= y.
A appartient au cercle ; x2 +y2 = 1 ; 2y2 = 1 ; y = 0,5½.
AB = BC = 2 *0,5½ =2½.
Question 5.
On suppose l’espace muni d’un repère orthonormé. Soient P le plan d’équation cartésienne 2x + y −z −3 = 0, A le point
de coordonnées (−1 ;1 ;−4) et D la droite d’équation paramétrique :
x = −1+2t
y = 1+t
z = −4−t avec t réel.
On admet que A appartient à P et que D est la droite perpendiculaire au plan P passant par A.
Soit B le point de D de coordonnées (3 ;3 ;−6). Si C est un point du cercle inclus dans P de centre A et de rayon 5, alors
BC =
a. 6 ; b. 7 vrai; c. 36 ; d. 49.
Equation du cercle : (x+1)2 +(y-1)2+(z+4)2 = 25.
C appartient au cercle : (xC+1)2 +(yC-1)2+(zC+4)2 = 25.
xC2 +yC2 +zC2 +2xC -2yC+8zC =7.
xC2 +yC2 +zC2 = -2xC +2yC-8zC +7.
BC2 = (xC-3)2+(yC-3)2+(zC+6)2 =xC2 +yC2 +zC2 -6xC -6yC+12zC +54.
BC2 = -8xC -4yC+4zC +61 = -4(2xC +yC-zC )+61.
C appartient au plan P : 2xC + yC −zC −3 = 0.
2xC + yC −zC = 3.
BC2 = -4 * 3 +61 = 49 ; BC = 7.