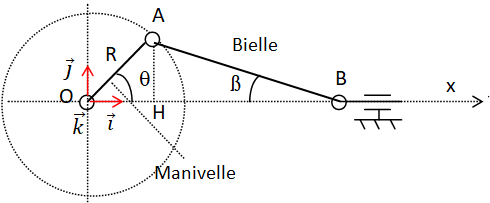
Mécanique , bielle, bille reliée à deux fils, EMIG ( école des mines, de l'industrie et de la géologie).

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.


.
.
.. ..
......


...
Système bielle manivelle.

q = wt ; AB = L ; k = L / R. w est constante.
1. Déterminer les expressions de la position du point A.
x =R cos q = R cos ( wt) ; y =R sin q = R sin ( wt) ;  z = 0.

2. Exprimer l'angle ß en fonction de q.
Dans le triangle OAH : sin q =AH / R ;
Dans le triangle ABH : sin ß =AH / L ;
sin ß =R / L sin q = sin q / k.
3. Déterminer les expressions de la position du point B en fonction de w, t, R et k.
x = OB ; y = z = 0.
Dans le triangle OAH : cos q =OH / R ;
Dans le triangle ABH : BH2 =L2 -AH2=L2 -R2 sin 2q.
OB =R cos q +(L2 -R2 sin 2q)½ ;
OB =R cos q +(k2 R2 - R2 sin 2q)½ ;
OB =R[ cos(wt) +(k2  -  sin 2(wt))½ ].

4. Déterminer les expressions des vecteurs vitesses linéaires des points A et B en fonction  de w, t, R et k.
Point A : vx = x' = -Rw sin( wt) ;
vy = y' = Rw cos( wt).
v = (vx2 +vy2)½ = R w.
Point B :  vx =R[ -w sin( wt) -w sin( wt) cos( wt) /  (k2  -  sin 2(wt))½ ].
vx = -R w sin( wt) [1+  cos( wt) /  (k2  -  sin 2(wt))½ ].

 5. Déterminer les expressions des vecteurs accélérations normale et tangentielle du point A. En déduire la force d'inertie exercée sur la manivelle  par une masse m concentrée en A. Représenter cette force sur un schéma.
ax = x'' = -Rw2 cos( wt) ;
ay = y'' = -Rw2 sin( wt).
a =(ax2 +ay2)½= Rw2 .
Dans  la base de Frenet : an =v2 / R = Rw2  et at = dv / dt =0, w étant constant.
La force d'inertie est centrifuge F = -m an.

 6.  Déterminer les expressions du vecteur accélération linéaire du point B. En déduire la force d'inertie exercée sur la bielle si m2 est la masse du piston.
Dériver vx en posant u = -R w sin( wt) et v = [1+  cos( wt) /  (k2  -  sin 2(wt))½ ]
u' = -R w2 cos( wt) ;
on pause a = cos( wt) et b =(k2  -  sin 2(wt))½ .
a' = - w sin( wt) ; b' =  -w sin( wt) cos( wt) / (k2  -  sin 2(wt))-½ .
v' = (a' b-b' a) / b2 =[- w sin( wt)(k2  -  sin 2(wt))½ +w sin( wt) cos2( wt) / (k2  -  sin 2(wt))-½ ] / (k2  -  sin 2(wt)).



Force d'inertie F = -m2 ax.

...
....

 Une petite bille M de masse m est reliée à deux points A et A' d'un axe vertical par l'intermédiaire de 2 fils MA et MA' inextensibles et sans masse tels que MA = MA' =L. L'axe tourne sur lui même avec une vitesse angulaire constante w telle que q = wt. Les deux fils sont tendus pendant le mouvement et forme avec l'axe AA' un angle a.


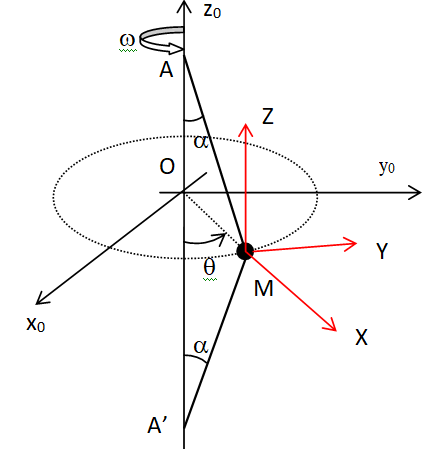
1. Déterminer les expressions des accélérations relative, d'entraînement et de Coriolis du point M par rapport au repère fixe (O, x0, y0, z0). En déduire les forces d'inertie correspondantes.
La rotation étant uniforme ( w = constante), l'accélération de Coriolis est nulle ; il en est de même de la force d'inertie de Coriolis.
Accélération d'entraînement : ae = w2 OM
Force d'inertie d'entrainement centrifuge de norme mw2 OM.

2. Faire le bilan des forces extérieures appliquées à M et écrire le principe fondamental de la dynamique dans le repère galiléen (O, x0, y0, z0).

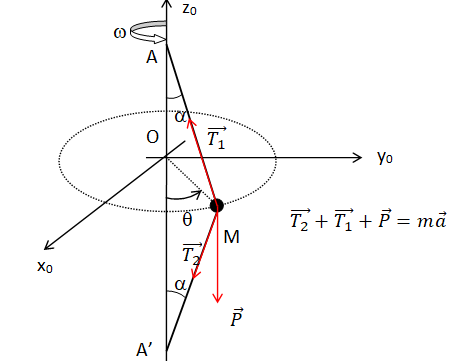
Tensions des deux fils et poids.
3. Ecrire le principe fondamental de la dynamique dans le repère (M, X, Y, Z). En déduire les tensions des deux fils.
 Projections sur l'axe vertical Oz : T1 cos a -T2 cos a -mg = m az= 0.
T1- T2 = mg / cos a.(1)
Dans la base de Frenet, projections sur OM : T1 sin a +T2 sin a = m v2 / OM = m w2 OM =m w2 Lsin a.
T1+T2=m w2 L. (2)
(1) +(2) donne : T1 = ½ m (w2 L+mg / cos a).
Par suite T2 =½ m (w2 L-mg / cos a).

Chimie.
1. Quelle est la différence entre 147N et 15 7N ?
Composition des noyaux :
147N  : 7 protons et 7 neutrons.
 15 7N : 7 protons et 8 neutrons.
Ils ne diffèrent que par leur nombre de neutrons ; ce sont deux isotopes.

 2. Donner la configuration électronique de 92U à l'état fondamental.
1s2, 2s2, 2p6, 3s2, 3p6, 4s2, 3d10, 4p6, 5s2, 4d10, 5p6, 6s2, 4f14, 5d10, 6p6, 7s2, 5f3, 6d1.
3.  Donner la configuration électronique de 79Au, 80Hg et 82Pb à l'état fondamental.
79Au : 1s2, 2s2, 2p6, 3s2, 3p6, 4s2, 3d10, 4p6, 5s2, 4d10, 5p6, 4f14, 5d10, 6s1,
 80Hg  : 1s2, 2s2, 2p6, 3s2, 3p6, 4s2, 3d10, 4p6, 5s2, 4d10, 5p6, 4f14, 5d10, 6s2.
et 82Pb : 1s2, 2s2, 2p6, 3s2, 3p6, 4s2, 3d10, 4p6, 5s2, 4d10, 5p6, 4f14, 5d10, 6s2, 6p2.

4. Expliquer la formation des liaisons dans  :
HCl : liaison covalente polarisée ; l'atome de chlore porte une charge partielle négative.
H3O+ : l'atome central d'oxygène établit 3 liaisons de covalence avec 3 atomes d'hydrogène.
PCl5 : molécule bipyramidale à base triangulaire,  hybridation sp3d pour le phosphore.
BF4- : géométrie tétraèdrique ; il se forme par action de sels de fluorures avec le trifluorure de bore.
[Co(NH3)6]2+ : réaction acide base selon Lewis Co3+ + 6NH3.

  
menu