Mathématiques,
concours interne ingénieur territorial 2011.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Problème 1.
Soit l'endomorphisme f de R3 représenté par la base canonique (e1, e2, e3) par la matrice A.
1.a Soit le vecteur u=(0 ; 1 ; -1). Calculer f(u).
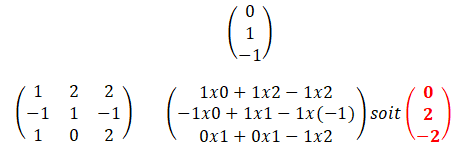
1.b. Que peut-on en déduire pour u et le réel 2 ?
f(u) = 2 u.
Donc u est un vecteur propre de f associé à la valeur propre 2.
2. On note l1, l2, l3 les valeurs propres réelles de f, rangées par ordre croissant. 2.a Calculer les valeurs propres de f .
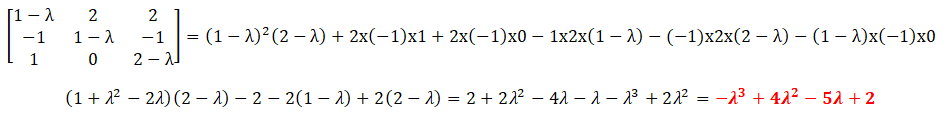
Résolution de -l3 +4l2 -5l +2=0.
2 est une racine.
(l-2)( al2+bl+c) = 0
On identifie al3= -l3; a = -1.
-2c =2 ; c = -1.
(l-2)( -l2+bl-1) = 0.
2l2+bl2=4l2 ; b =2.
Solutions de -1l2+2l-1) = 0.
Discriminant D =22-4(-1)(-1) =0.
Racine double : l = 1.
Valeurs propres de f : l1=l2=1 ; l3=2.
2.b Soit E 1 le sous espace propre associé à l1. Montrer que E 1 est de dimension 1.
On note v=(x, y, z) un vecteur propre associé à l1. Donc A u = 1 u ou Au-u=0.
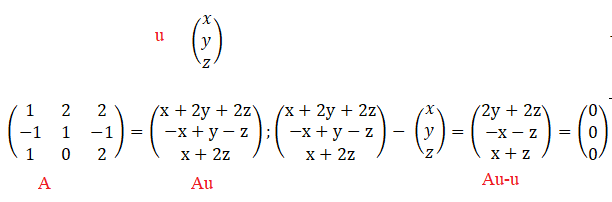
Soit y+z = 0 et x+z = 0.
Le sous espace E1 est une droite de l'espace. Sa dimension est donc 1.
2.c. Donner un vecteur propre v associé à la valeur propre l1.
Solutions du système t y+z = 0 et x+z = 0.
x = k ; z = -k ; y = k avec k un nombre réel.
Par exemple v = (1 ; 1 ; -1).
2.d. Expliquer pourquoi A n'est pas diagonalisable.
On a trouvé une valeur propre double ( l1 = 1) et que le sous espace associé E1 a la dimension 1.
La somme des dimensions des sous-espaces propres ( soit 2) diffère de la dimension de R3 ( soit 3). Donc A n'est pas diagonalisable.
3. Soit le vecteur v = (1 ; 1 ; -1).
3.a. Vérifier et justifier que (u, v, e3) forme une base de R3. On note B' cette nouvelle base.
On calcule le déterminant Det(u, v, e3).
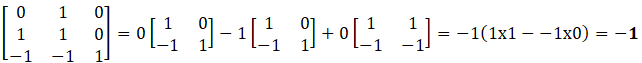
Le déterminant n'étant pas nul, u, v et e3 sont des vecteurs linéairement indépendants d'un espace de dimension 3. Ils constituent une base de R3.
3.b. Calculer les coordonnées de f(u) et f(v) dans la base B'.
f(u) = 2x u.
Les coordonnées de u dans la base B' sont u=(2 ; 0 ; 0).
De même f(v) = 1 x v.
Les coordonnées de v dans la base B' sont v=(0 ; 1 ; 0).
3.c En déduire qu'il existe une matrice inversible M et une matrice triangulaire supérieure T telles que :
A = M-1T M.
Expliciter M et T.
On rappelle qu'une matrice triangulaire supérieure est telle que tous les éléments situés sous sa diagonale valent 0.
Dans la base B', f est représentée par les vecteurs colonnes f(u)=2 x u, f(v) = 1 x v et f(e3).
e1=(1 ; 0 ; 0) ; e2=(0 ; 1 ; 0) ; e3=(0 ; 0 ; 1).
u =(0 ; 1 ; -1) soit u = e2-e3.
v=(1 ; 1 ; -1) soit v=e1+e2-e3.
La matrice M de passage de B à B' est la matrice des nouveaux vecteurs de base exprimés en fonction des anciens.
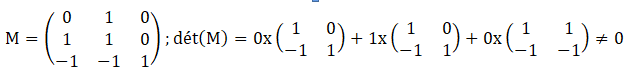
Le déterminant de M n'est pas nul, donc M est inversible.
Quand à la matrice T :
Par suite e1 = v-u ; e2=u+e3.
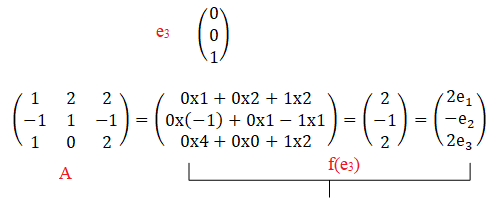
f(e3) = 2e1-e2+2e3 =2v-2u-(u+e3)+2e3 = -3u+2v+e3.
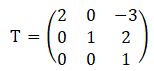
|
...
|
....
|
Problème 2.
L'étude d'un phénomène d'amortissement conduit à l'équation différentielle (E) :
y" +2y'+2y=0.
où y est une fonction de la variable x, définie et 2 fois dérivable sur R.
1. Résoudre (E) sur R.
Equation caractéristique : r2+2r+2=0.
Discriminant D = 22-8=-4 = 4 i2.
Racines complexes : r = (-2 ±2i) / 2 = -1 ± i.
Solution de (E) : y = Ae-x cos(x+B) où A et B sont des constantes.
2. Déterminer la solution de (E) vérifiant y(0) = 0 et y'(0) = 1.
y(0) = Acos B= 0 soit B = (2k+1) p / 2 ou A = 0.
Calcul de y' en posant u = A e-x et v = cos(x+B) ;
u' = -Ae-x ; v' = -sin(x+B).
y' = u'v +v'u = -Ae-x cos(x+B) -A e-xsin(x+B).
y'(0) = -Acos B -A sinB = -A(cos B + sin B) = 1.
A diffère donc de zéro.
or cos B = 0 et sin B =±1 ; A sin B = -1 ;
A = 1 et B =3p/2 ou bien A = -1 et B = p/2.
y = e-x cos(x+3p/2) =e-x sin (x).
3. On considère la fonction f définie sur [0 ; p] par f(x) = e-x sin x.
On note G sa courbe représentative dans un repère orthogonal.
3.a Vérifier que cos x-sin x = 2½ sin ( p/4-x) pour tout x de cet intervalle.
sin (a-b) = sin a cos b -cos a sin b avec a = p/4 et b = x.
sin ( p/4-x) =sin (p/4) cos x -cos (p/4) sin x =2½ / 2 ( cos x - sin x) = ( cos x - sin x) / 2½.
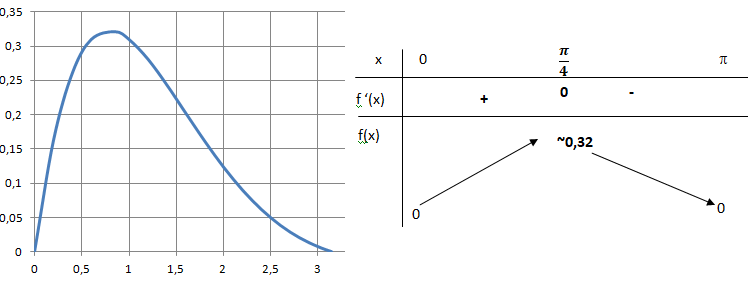
3.b Etudier les variations de f et dresser son tableau de variations.
Calcul de f '(x) en posant u = e-x et v = sin x ; u' = -e-x ; v' = cos x.
f '(x) = e-x(cos x- sin x )= 2½e-x sin ( p/4-x).
2½e-x étant strictement positif le signe de f '(x) est celui de sin ( p/4-x).
si x < p/4, f '(x) >0 et f est strictement croissante.
si x > p/4, f '(x) <0 et f est strictement décroissante.
Si x = p/4, f '(x) =0 et f présente un maximum.
3.b.
Ecrire un développement limité de f au voisinage de 0 à l'ordre 3. En
déduire l'équation de la tangente T à la courbe au point d'abscisse 0
et donner la position relative de T et G.
e-x =1 -x+x2/2-x3 / 6.
sin x =x-x3/6.
e-x sin x =(x-x3/6)(1 -x+x2/2-x3 / 6).
En se limitant à l'ordre 3 :
e-x sin x =x -x2+x3/2-x3/6 = x -x2+x3/3.
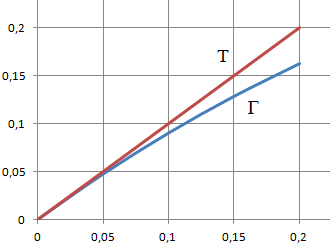
Equation de la tangente à l'origine : y = x.
y-x = -x2+x3/3 < 0 au voisinage de zéro.
La courbe est en dessous de la tangente.
4. Construire la courbe G et la tangente T.
5.
En utilisant le fait que f est une solution de l'équation
différentielle (E), déterminer une primitive F de f sur cet intervalle.
y" +2y'+2y=0.
f = -0,5f "- f '.
F = -0,5 f ' -f.
F = -0,5 e-x(cos x- sin x )- e-x sin x.
F(x) = -0,5 e-x(sin x + cos x).
6. En déduire l'aire du domaine délimité par la courbe G et l'axe des abscisses.
Aire =F(p)-F(0).
F(0) = -0,5.
F(p) =0,5 e-p.
Aire =0,5( e-p+1) ~ 0,52 unités d'aire.
|
|