Mathématiques, concours interne ingénieur territorial 2013. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... Problème 1. Une société entreprend la réalisation de pièces métalliques de forme cylindrique dont on donne le schéma ci - dessous. 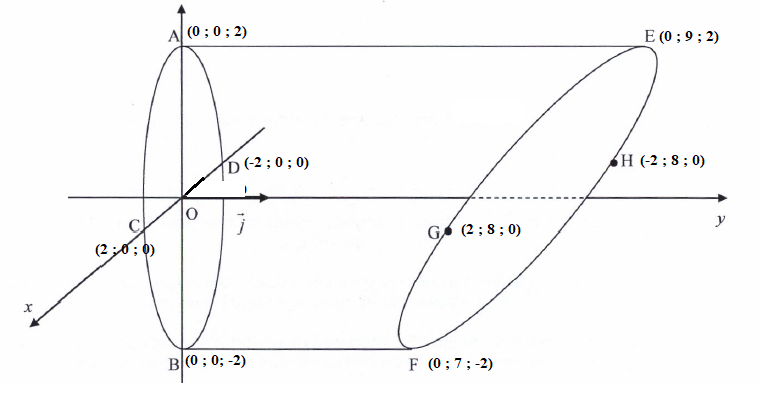(Ce dessin n'est pas à l'échelle.) Ces pièces sont sectionnées à chaque extrémité selon les ptans (ABC) et (EFG) . On donne, dans ce repère les points : Question 1 : (0,75 point) Calculer les longueurs AB, AE et BF. AB = 4 ; AE = 9 ; BF= 7. Question 2 : (0,75 point) a) Calculer les coordonnées du vecteur suivant. 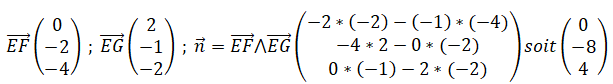b) En déduire une équation cartésienne du plan (EFG) Equation cartésienne du plan (EFG) : 0 x -8y +4z +d = 0. G(2 ; 8 ; 0) appartient à ce plan : 2*0-8*8+4*0+d= 0 ; d =64. -8y +4z +64 = 0. -2y+z+16=0. Question 3 : (1,5 points) Vérifier que le quadrilatère AEFB est un trapèze rectangle. AE et BF sont parallèles et perpendiculaires à AB. Soit K le projeté orthogonal de F sur [AE] . Câlculer le produit scalaire suivant, et en déduire à 0,1 degré près, une mesure de I'angle KFE. 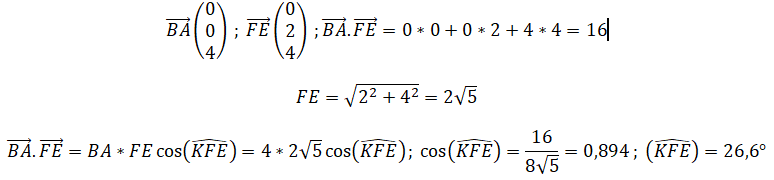Question 4:(2polnts) On donne ci - dessous le développement de l'une des pièces métalliques. Le repère  est orthonormal d'unité 1 cm. (Le dessin n'est pas à l'échelle.) On admet que, dans ce repère la courbe obtenue a pour équation : y = 8 + cos(0,5 x). 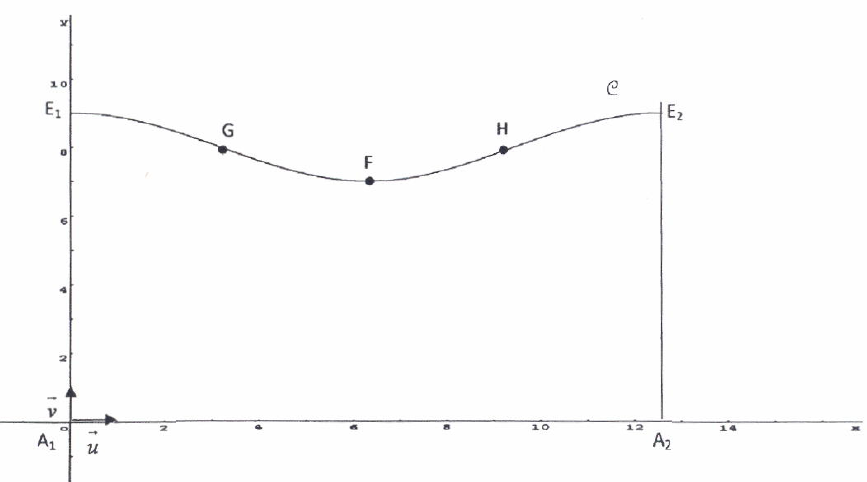a) Justifier que le segment [A1A2] a pour longueur 4p. A1E1 = 8 +cos(0) = 9. A2E2 = 8 +cos(a) = 9 ; cos(a) =1 ; a =2p (2p)=0,5 x ; x =4p. b) Calculer l'aire en cm2 de la surface métallique A1A2E2E1 . On donnera la valeur exacte, puis une valeur approchée au mm2 près. 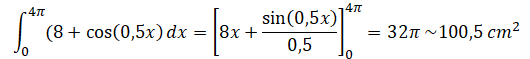c) Retrouver cette aire par une autre méthode en utilisant les propriétés du cylindre. Aire latérale du cylindre de rayon 2 cm et de hauteur moyenne ( BF + AE) / 2 = 8 cm : 2 pr ( BF + AE) / 2 =32 p cm2. ... .... Problème 2. Soit l'endomorphisme f de R3 représenté par la base canonique B0(e1, e2, e3) par la matrice A. 1. Déterminer les valeurs propres de A, une base et la dimension de chaque sous-espace propre. Résoudre -l3 -l=0 ; racines  l1 = i ; l2=-i ; l3=0. Pour chaque valeur propre, il faut trouver un vecteur X tel que AX = l X. Ei de dimension 1 et de base par exemple (1 ; -1-i ; -1-i) ; en multipliant ce vecteur par une constante, c'est encore une solution. E-i de dimension 1 et de base par exemple (1 ; -1+i ; -1+i). E0 de dimension 1 et de base par exemple (-1 ; 1 ; 0). 2. La matrice est-elle inversible ? Diagonalisable ? Le polynôme caractéristique de A est scindé en racines simples : donc A est diagonalisable. La famille formée par les vecteurs propres de la matrice est libre, donc A est inversible. 3. On pose u1 = e1-e2 ; u2 = f(e2) ; u3 = f(e3). 3.a  Prouver que B1=(u1 ; u2 ; u3) est une base de R3. Ecrire la matrice de passage P de la base B0 à la base B1. e1 (1 ; 0 ; 0) ; e2 (0 ; 1 ; 0) ; u1 (1 ; -1 ; 0). Les vecteurs u1 ; u2 ; u3 sont libres : B1=(u1 ; u2 ; u3) est une base de R3. 3.b Vérifier que P-1 est la matrice suivante. Déterminant de B1 : 1*2*(-1) +-1*(-1)*0+0*2*(-1)-[0*2*0+(-1)*(-1)*(-1)+1*2*(-1)]= -2+3=1. Transposer la matrice : la première rangée devient la première colonne ... Déterminer la matrice des cofacteurs. Diviser chaque terme par le déterminant. 3.c. Démontrer les égalités f(u1)=0 ; f(u2) = u2+2u3 ; f(u3)= -u2-u3. En déduire la matrice B de f dans la base B1. 3.d. Calculer B2 et en déduire B2n pour n > 1. B2n = B2. 4. Démontrer par récurrence que pour tout entier naturel n > 1, on a : A2n = PB2n P-1. Initialisation : A2 = PB2 P-1 est vrai. Hérédité : A2n = PB2n P-1 est supposé vrai. A2n A2=A2(n+1)= PB2n P-1 A2= PB2n P-1PB2 P-1 =PB2n B2 P-1 =PB2(n+1)  P-1 . La propriété est vraie au rang n+1 Conclusion : la propriété est vraie au rang 1 et héréditaire, elle est donc vraie pour tout entier naturel n > 1. 5. En déduire l'expression de A2n et de A2n+1. A2n = PB2 P-1. A2n A= PB2 P-1A.

menu