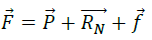Télémètre
à ultrasons, bac Asie 2022.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Le
télémètre à ultrasons permet de déterminer la position d’un objet en
mesurant la durée nécessaire à une salve d’ultrasons pour faire un
aller-retour entre un module télémètre et l’objet sur lequel la salve
d’ultrasons se réfléchit.
Dans cet exercice, on
s’intéresse au principe de la mesure de distances avec le télémètre
(Partie A). Dans un second temps, on utilise le télémètre pour faire
des relevés conduisant à évaluer la valeur d’une force de frottement
(Partie B).
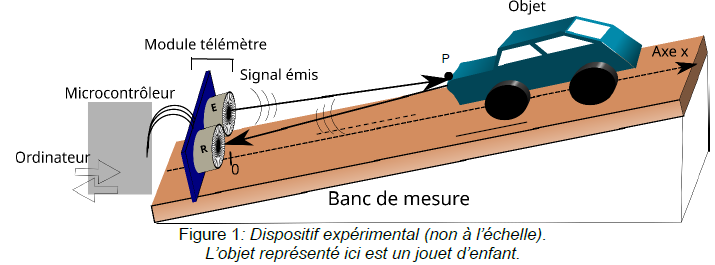
On
suppose que la distance entre le télémètre à ultrasons et l’objet est
grande devant la distance entre l’émetteur E et le récepteur R. Ainsi,
on peut considérer que la salve suit quasiment l’axe (𝑂𝑥), à l’aller
et au retour, et que la distance donnée par le télémètre est égale à
l’abscisse 𝑥 du point P de l’objet sur lequel se réfléchit la salve
d’ultrasons : EP=PR=𝑥.

Partie A – Principe de la mesure de distance avec le télémètre
Le module télémètre est constitué d’un émetteur (E) et d’un récepteur
(R). Il est relié à un microcontrôleur qui commande l’émission de la
salve d’ultrasons par l’émetteur et traite le signal reçu par le
récepteur pour en déduire l’intervalle de temps Dt mis par la salve d’ultrasons pour faire l’aller-retour. Le microcontrôleur échange les données avec un ordinateur.
1. Montrer que la relation liant la distance x à la durée Dt nécessaire à l’aller-retour de la salve d’ultrasons est :
x = ½vs Dt (1)
où vs est la vitesse de propagation des ultrasons dans l’air.
Distance aller + retour = 2 x = vs Dt ; x = ½vs Dt.
2.
Identifier la ligne du programme Python permettant de passer de
la durée mesurée à la distance x et préciser l’unité dans laquelle le
programme calcule la valeur de x.

Ligne 12 ; x est exprimée en mètre.
Calibrage du télémètre et précision des mesures.
Pour pouvoir réaliser des mesures avec le télémètre étudié, il est
nécessaire de connaître la vitesse des ultrasons dans l’air. Or, cette
vitesse dépend de la température de l’air. Afin de remédier à cette
difficulté, on met en oeuvre une démarche de type « calibrage » avant
d’utiliser le télémètre pour réaliser des mesures de distance. En
pratique, ce calibrage consiste à déterminer la vitesse des ultrasons
grâce au télémètre.
3. À l’aide de la
relation (1), proposer un protocole expérimental permettant de
déterminer la vitesse des ultrasons dans l’air à l’aide du télémètre.
vs = 2x / Dt.
On mesure Dt pour une distance x connue.
Pour
affiner la précision de la mesure de la vitesse des ultrasons, le
protocole de calibrage est réalisé à 5 reprises. Le tableau ci-dessous
donne les résultats successifs pour la valeur de la vitesse des
ultrasons dans l’air :
Mesure n°
|
1
|
2
|
3
|
4
|
5
|
vs ( m /s)
|
349
|
352
|
348
|
347
|
351
|
Pour la série de mesures, la valeur de l’écart-type donnée par la calculatrice est : s = 2,07 m·s-1.
4. Calculer la
valeur moyenne de la série de mesures. Montrer, en conservant un nombre
adapté de chiffres significatifs, que le résultat de la mesure de la
vitesse des ultrasons dans l’air peut s’écrire :
vs=349,4±0,9 m·s−1 (2).
u(vs) =s / n½ = 2,07 / 5½ =0,93 m /s ~0,9 m /s.
Valeur moyenne de la vitesse : (349 +352 +348 +347 +351) / 5 =349,4 m /s.
vs=349,4±0,9 m·s−1.
5. Indiquer la ligne et la modification à faire pour tenir compte de la valeur moyenne de vs établie à la question 4.
Ecrire à la ligne 6 : vs=349,4 # vitesse des ultrasons en m /s.
Au niveau du microcontrôleur, la durée de l’aller-retour d’une salve d’ultrasons est déterminée avec une incertitude : u(Dt)=10 μs.
Lors d’une mesure de distance x, le télémètre mesure une durée Dt=3438 μs.
6. Calculer la
valeur de x déterminée par le télémètre à l’issue du calibrage
précédent. Estimer la valeur de l’incertitude de mesure u(x) et écrire
le résultat de la mesure avec un nombre adapté de chiffres
significatifs.
x =349,4 x3438 10-6 / 2 = 0,6006 m.
u(x) / x = [(u(vs) / vs)2 +(u(Dt) / Dt)2]½ =[(0,9 / 349,4)2 +(10 / 3438)2]½ =(6,63 10-6 +8,46 10-6)½~ 4 10-3.
u(x) =0,6006 x 4 10-3 ~3 10-3 m.
x = (601 ±3)10-3 m.
|
...
|
....
|
Partie B - Estimation de la valeur d’une force de frottement
On utilise le télémètre à ultrasons pour étudier le mouvement d’une
voiture d’enfant posée sur un plan incliné. Par cette étude, on
souhaite estimer la valeur f de la résultante de l’ensemble des forces
de frottement appliquées sur la voiture en mouvement.
Un traitement des données permet d’obtenir la position du centre de
masse du système {voiture}. Dans cette partie B, x désigne l’abscisse
du centre de masse.
L’étude des relevés expérimentaux dans le cadre de la mécanique de
Newton permet de tendre vers l’estimation recherchée de deux manières
différentes.
Le système {voiture} est lâché sans vitesse initiale à la position x0=56,0 cm sur un banc de mesure incliné d’un angle a
par rapport à l’horizontale. On constate que le mouvement du centre de
masse du système {voiture} est rectiligne le long de l’axe (Ox) et
accéléré dans le sens du déplacement ( vers O).
L’étude est menée dans le référentiel terrestre considéré comme étant galiléen.
Le système est soumis à :
son poids P, verticale vers le bas valeur mg.
la réaction du support N, perpendiculaire au plan incliné (donc suivant (𝑂y) ), sens : vers les y positifs,
des forces de frottements représentées par leur résultante f : tangente
au plan incliné (donc suivant (Ox) ), sens opposé au mouvement, vers
les 𝑥 positifs, valeur : f.
On note F la résultante des forces extérieures exercées sur le système {voiture}.
Une étude des forces, non demandée ici, permet d’établir :
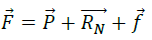
On fait l’hypothèse que f (et donc F) est constante au cours du mouvement.
Intensité du champ de pesanteur terrestre : g = 9,81 m·s-2.
Masse de la voiture d’enfant : m = 103 g.
Angle d’inclinaison du plan incliné : a = 40°.
7. À l’aide de la
description du mouvement, déterminer la direction et le sens du vecteur
accélération a (𝑡) du centre de masse du système {voiture}.
Direction : Ox ; sens : vers O, la vitesse initiale est nulle et la vitesse augmente ( mouvement accéléré )..
8. Enoncer la deuxième loi de Newton.
La somme des forces extérieures appliquées au système est égale au
produit de la masse du système par le vecteur accélération de son
centre de masse.
9. En déduire la direction et le sens de la résultante des forces F.
F a le sens du vecteur accélération ( suivant Ox, dirigée vers O).
Etude mécanique :
L’étude est menée le long de l’axe (Ox).
10. Montrer que l’équation horaire du mouvement du centre de masse du système s’écrit :
x(t) =-½F / m t2 + x0. (4)
a = - F / m ; la vitesse est une primitive de l'accélération : v = -at + Cste.
La vitesse initiale étant nulle : v = -at = -F / m t.
La position est une primitive de la vitesse : x = -½F / m t2 + Cste.
La position initiale étant x0 : x(t) =-½F / m t2 + x0.
Les relevés expérimentaux de x(𝑡) sont présentés sous la forme d’un graphique.
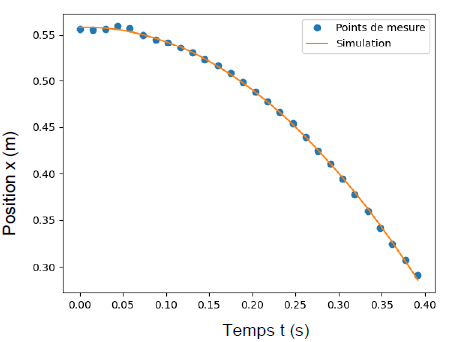
Le tableur utilisé permet de superposer aux points de mesure une modélisation par un polynôme d’équation :
x(t) = -1,84t2 +0,558.
11. Indiquer si la valeur obtenue pour le coefficient 0,558 est cohérente avec les données du problème.
x = 0,56 m, valeur cohérente avec 0,558 ( écart relatif : 0,4 %).
12. À partir de la modélisation des points expérimentaux, montrer que la valeur f de la force de frottement est voisine de 0,27 N.
la seconde loi de Newton projetée sur l'axe Ox donne : -f + mg sin a =m a.
a = 1,84 x 2 = 3,68 m s-2.
f = m(g sin a - a )= 0,103 ( 9,81 x sin 40 -3,68)=0,27 N.
Etude énergétique :
Pour compléter l’étude mécanique, on se propose d’estimer f par une
étude énergétique entre le point A où la voiture a été lâchée sans
vitesse initiale (𝑥𝐴=𝑥0=56,0 cm) et le point B d’abscisse 𝑥𝐵=35,0 cm.
13. Enoncer le théorème de l’énergie cinétique entre les positions A et B.
La variation de l'énergie cinétique est égale à la somme des travaux des forces appliquées au système.
14. Exprimer le travail WAB(𝐹 ) de la résultante des forces F entre A et B en fonction de m, g, f, a et d=𝑥𝐴−𝑥𝐵.
F = mg sin a -f ; WAB(𝐹 ) = F d = (mg sin a -f) d.
Les données
acquises sur la position du centre de masse permettent de calculer la
valeur de la vitesse du centre de masse au point B en considérant deux
points au voisinage du point B. On obtient : 𝑉𝐵=1,21 m∙s−1.
15. Proposer une nouvelle estimation de la valeur de f.
½m vB2 - 0 = (mg sin a -f) d.
f = mg sin a -½m vB2 / d =m (g sin a -½ vB2 / d) = 0,103 ( 9,81 x sin 40 -0,5 x1,212 /0,21)=0,103( 6,3-3,48) =0,29 N.
|
|