Contrôle
de l'ordre d'une réaction,
bac général Asie
2023.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| .. |
.
.
|
|
.
.
|
..
..
......
...
|
En solution aqueuse le peroxyde d'hydrogène H2O2 peut se décomposer en eau et dioxygène.
H2O2 aq --> H2O(l) + ½O2(g) (1).
Cette réaction est lente, accélérée par les ions Fe3+aq.
H2O2 aq + 2Fe3+aq -->2Fe2+aq +O2(g) +2H+aq étape 1.
H2O2 aq + 2Fe2+aq +2H+aq--> 2Fe3+aq +2 H2O(l) étape 2.
1. Justifier que l'ion fer (III) joue le rôle de catalyseur.
Cet ion n'apparaît pas dans le bilan : il réagit lors de l'étape 1 et se trouve régénéré à l'étape 2.
On réalise le dosage par titrage, à différentes dates, d'un échantillon du milieu réactionnel par les ions permanganate MnO4-. Chaque dosage permet de déterminer la concentration en H2O2 restant à la date t.
L'équation support du titrage est :
5H2O2 aq +2 MnO4-aq + 6H+aq -->5 O2(g) + 2Mn2+aq+8 H2O(l) (2).
MnO4- est la seule espèce chimique colorée.
Protocole :
On dispose :
- d'une solution S0 d'eau oxygénée de concentration inconnue C0.
- d'une solution de chlorure de fer (III) de concentration 0,1 mol / L.
- D'une solution SP depermanganate de potassium de concentration Cp = 2,00 10-2 mol / L.
- d'une solution d'acide sulfurique.
Remplir la burette graduée avec la solution de permanganate de potassium.
Préparer 7 erlenmeyers contenant chacun 40 mL d'eau distillée glacée et 10mL de solution d'acide sulfurique.
Les placer dans un cristallisoir contenant un mélange d'eau et de glace.
Dans un erlenmeyer de 150 mL verser 95,0 mL de la solution S0.
Introduire un barreau aimanté, placer l'ensemble sur un agitateur et mettre en route l'agitation.
Verser rapidement 5 mL de solution de fer (III) et déclencher le chronomètre.
Prélever rapidement un volume VR = 10,0 mL du milieu
réactionnel. Verser rapidement dans l'un des 7 erlenmeyers. Introduire
le barreau aimanté et doser par titrage le peroxyde d'hydrogène
présent dans le volume VR à cette date par la solution de permanganate. Noter le volume équivalent VE.
Procéder de la même façon aux dates 4 min, 6 min, 8 min, 12 min, 20 min, 40 min et 80 min.
t(min)
|
1,75
|
4
|
6
|
8
|
12
|
20
|
30
|
40
|
80
|
VE(mL)
|
16,0
|
15,0
|
13,8
|
12,9
|
11,4
|
8,3
|
5,9
|
4,2
|
1,2
|
[H2O2]mmol / L
|
80,0
|
75,0
|
69,0
|
64,5
|
|
43,0
|
29,5
|
21,0
|
6,0
|
2. Identifier les deux facteurs cinétiques mis en oeuvre pour stopper la réaction de dismutation (1) le temps du dosage.
La température est un facteur cinétique. Le bain d'eau glacé réalise un blocage cinétique.
3. Indiquer le changement de couleur observer à l'équivalence.
Avant l'équivalence l'ion permanganate est en défaut : solution incolore.
Après l'équivalence l'ion permanganate est en excès : solution violette.
4. Etablir la relation suivante : [H2O2]=5 Cp VE / (2 VR).
A l'équivalence : quantité de matière d'ion permanganate : n =Cp VE.
Quantité de matière d'eau oxygénée titrée: [H2O2] VR = 2,5 n = 2,5Cp VE.
[H2O2]=2,5 Cp VE / VR.
5. calculer sa valeur à t =12 min.
[H2O2]=2,5 x2,00 10-2 x 11,4 / 10=0,57 mol / L = 57 mol / L.
6 Retrouver la relation d[H2O2] /dt = -k [H2O2], la cinétique étant d'ordre 1.
Vitesse volumique : v = -d[H2O2] /dt.
D'autre part pour une cinétique d'ordre 1 : v = k [H2O2] avec k une constante.
Par suite :d[H2O2] /dt = -k [H2O2].
La solution de cett équation différentielle est de la forme [H2O2](t) =B exp(-kt) relation 1.
7. Donner la signification physique de B.
A t = 0 : [H2O2](t=0) =B, concentration initiale en peroxyde d'hydrogène.
|
...
|
....
|
On a tracé les deux graphes suivants :
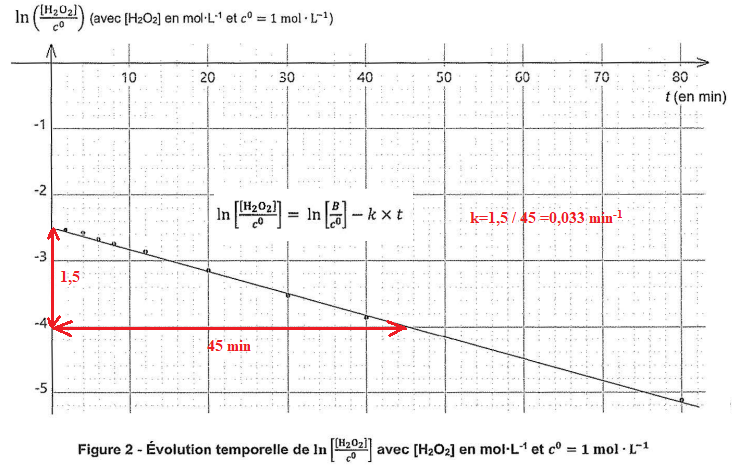
8. Montrer que l'hypothèse d'une cinétique d'ordre 1 est valide. En déduire k.
ln ([H2O2] / c°) -ln(B/c°) = -kt ;
ln ([H2O2] / B) = -kt ; [H2O2] / B = exp(-kt).
[H2O2] =B exp(-kt).
La courbe observée est une droite, la cinétique d'ordre 1 est valide.
9. Définir puis déterminer le temps de demi-réaction t½.
A t½, la concentration en eau oxygénée est égale à la moitié de la concentration initiale en eau oxygénée.
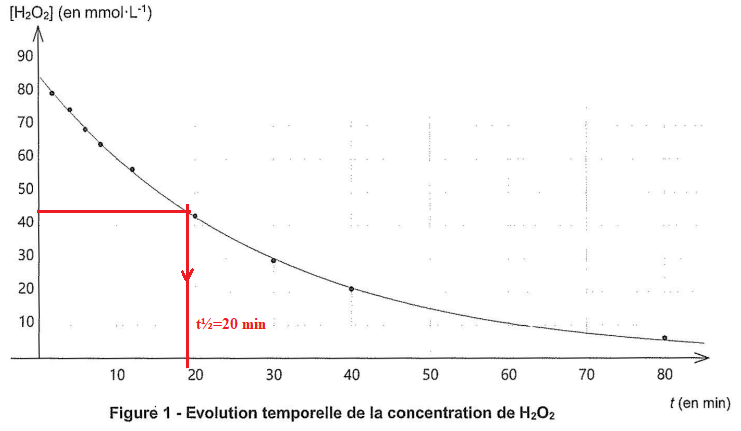
10. On donne pour une cinétique d'ordre1, la realtion k t½ = ln(2). La constante k dépend-elle de la concentrtaion initiale en eau oxxygénée ?
Pour
une réaction d'ordre1, le temps de demi-réaction ne dépend pas de la
concentration initiale en eau oxygénée ; il en est de même de la
constante k.
|
|