Transfert
thermique et gastronomie,
bac général Centres Etrangers SI
2023.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| .. |
.
.
|
|
.
.
|
..
..
......
...
|
À la sortie du réfrigérateur, le bloc de tomme
fraîche est retiré de son emballage puis posé sur
une de ses plus grandes faces, sur une planche en
bois. L’air circule alors librement tout autour des
cinq autres faces.
La situation sera modélisée en considérant
uniquement les transferts conducto-convectifs.
On néglige le transfert thermique au niveau de la
face du bloc en contact avec la planche en bois
devant les autres.
Pour simplifier, on considère que la température
du bloc de tomme notée q est la même en tout
point du bloc tout au long de l’expérience.
Une sonde thermique est insérée au cœur du bloc,
la température est enregistrée toutes les deux
minutes ; les résultats expérimentaux sont donnés.
1. Indiquer sur un schéma de la situation, faisant apparaitre les températures, dans quel sens
s’opère le transfert thermique au travers du bloc de tomme fraiche.
Le trandfert thermique s'effectue du corps le plus chaud ( l'air ambiant) vers le corps le plus froid ( la tomme).

En considérant uniquement les transferts conducto-convectifs, on admet que l’équation différentielle
vérifiée par la température du bloc de tomme fraiche est de la forme suivante :
dq
dt
+
h×S
/(m×c) q = h×S
/(m×c) qair (1)
Cette équation différentielle a pour solution générale : q(t) = qair+ (q0 - qair) × exp(- t / t) (2).
Q2. Vérifier à l’aide des équations (1) et (2) que t = m×c
/ (h×S). Donner la signification physique et l’unité
de cette grandeur.
Solution générale de dq
dt
+
h×S
/(m×c) q =0 :
q = A exp(-t h S / (m c)). A est une constante.
On identifie t = m c / (h S).
t est la constante de temps, exprimée en seconde. Elle nous renseigne sur la rapidité du réchauffement du bloc de tomme.
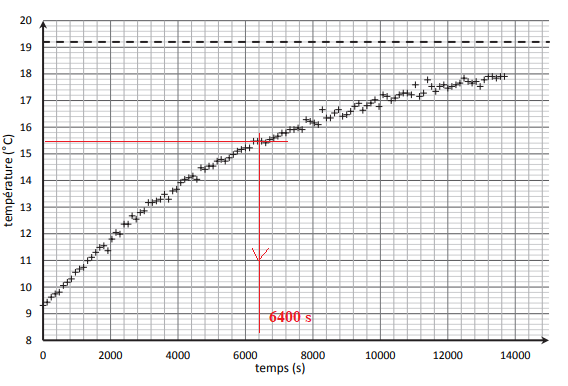
Q3. À l’aide de la figure 2, estimer, en explicitant la méthode, une valeur expérimentale de t, notée texp.
q(t= t) = qair+ (q0 - qair) × exp(-1)=15,5°C.
|
...
|
....
|
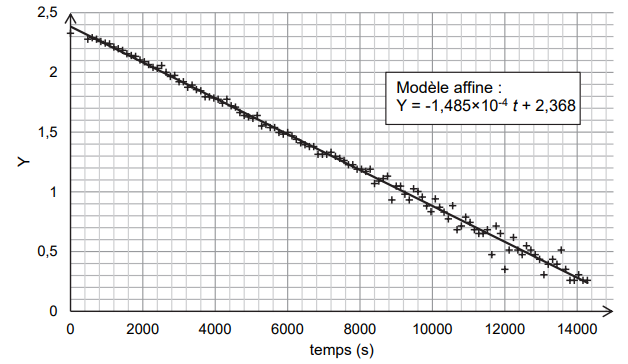
La représentation graphique de Y = ln(qair - q(t)) en fonction du temps est donnée sur la figure suivante, ainsi que sa modélisation par une fonction affine.
Q4. Montrer à l’aide de la figure que l’expression (2) rend bien compte des résultats
expérimentaux.
q(t) = qair+ (q0 - qair) × exp(- t / t)
qair - q(t) =(qair - q0) × exp(- t / t) = (19,2 - 9,2)exp(- t / t) = 10 exp(- t / t)
(qair - q(t)) / 10= exp(- t / t).
ln[(qair - q(t)) /10)] = - t / t.
ln[qair - q(t) ]-ln(-10) = - t / t.
Y =ln[qair - q(t) ] = - t / t + ln(10).
Il s'agit d'une fonction affine de pente négative.
Q5. Effectuer à l’aide de la figure 3 une nouvelle estimation de la valeur expérimentale de t et
comparer à celle obtenue à la question 3.
-1 / t = -1,485 10-4 ; t= 1 /(1,485 10-4) =6734 s.
Ecart relatif : (6734 -6400) / 6400 =0,05 ( 5 %).
Les valeurs sont en accord à 5 % près.
Q6. À partir des données, de l’expression t = m×c/(
h×S) et des valeurs expérimentales obtenues,
discuter des hypothèses du modèle choisi.
m = 0,52 kg ; c = 3,1 103 J kg-1 K-1 ; h = 10,0 W K-1 m-2 ; S = 2,9 10-2 m2.
mc / (hS) = 0,52 x3,1 103 /(10,0 x2,9 10-2)=5,56 103 s.
Ecart relatif : (6400 -5560) / 5560 =0,15 ( 15 %).
La montée réelle en température est plus longue que prévue.
La température a été mesurée au coeur du bloc qui se réchauffe moins vite.
Q7. Proposer une méthode permettant à un cuisinier de réduire la durée de la remontée en
température du bloc de tomme fraiche.
Couper le bloc en tranches fines ; ces tranches se réchaufferont plus vite.
|
|