Fonctions,
suites, spécialité mathématiques bac 2024.
.
|
.
.
|
L’exercice est constitué de deux parties indépendantes.
Partie I
On considère l’équation différentielle (𝐸)∶y'+y=e−𝑥.
1. Soit u la
fonction définie sur R par u(x)=xe-x.
Vérifier que la fonction u est une solution de l’équation
différentielle (E).
Calcul de u' en posant v = x et w = e-x ; v' = 1 ; w' = -e-x.
v'w+w'v = e-x -xe-x=e-x(1-x).
Repport dans (E) : e-x(1-x)+xe-x=e−𝑥
est vérifiée quel que soit x.
2. On considère
l’équation différentielle (E′)∶𝑦′+𝑦=0.
Résoudre l’équation différentielle (E′) sur R.
y = A e-x avec A une constante réelle.
3. En déduire
toutes les solution de l’équation différentielle (E) sur R.
f(x) =A e-x +u(x) =A e-x +xe-x.
4. Déterminer l’unique solution g de
l’équation différentielle (E) telle que g(0)=2.
A e-0
+0 e-0= 2 ; A = 2.
g(x) =2e-x
+xe-x.
Partie II
Dans cette partie, k est un nombre réel fixé que l’on cherche à
déterminer.
On considère la fonction fk définie sur R par fk(x))=(x+k)e-x.
Soit h la fonction définie sur R par h(x)=e−𝑥.
On note Ck la courbe représentative de la fonction fk
dans un
repère orthogonal et C la courbe représentative de la fonction H.
On a représenté les courbes Ck et C sans
indiquer les unités sur les axes ni le nom des courbes.
1. Sur le graphique
l’une des courbes
est en traits pointillés, l’autre est en trait plein. Laquelle est la
courbe C ?
2. En expliquant la
démarche utilisée, déterminer la valeur du nombre
réel k et placer sur l’annexe à rendre avec la copie l’unité sur
chacun des axes du graphique.
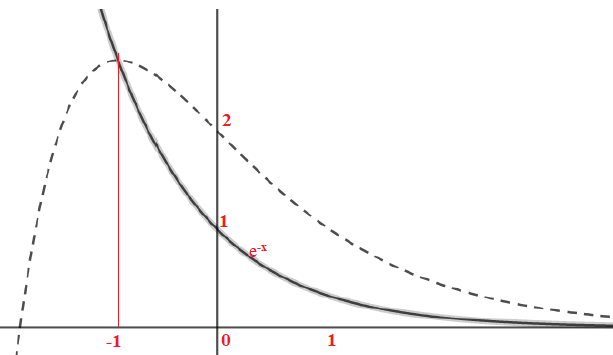
h(x)=e−𝑥 : quand x tend vers plus
l'infini, h(x) tend vers zéro ; quand x tend vers moins l'infini, h(x)
tend vers plus l'infini.
Quand x =0, h(0) = 1.
fk(x))=(x+k)e-x : quan x = 0, fk(x) = k = 2.
On dérive en posant u = x+2 et v = e-x ; u' = 1 ; v' = -e-x
; u'v+v'u = e-x -(x+2)e-x=e-x
(-x-1).
La dérivée s'annule pour x = -1 et fk(x)
présente un extrémum.
Exercice 2.
Partie I.
Pour tout entier 𝑛 supérieur ou égal à 1, on désigne par fn
la fonction définie sur [0 ;1] par : fn(x)=xnex.
On note Cn la courbe représentative de la fonction fn
dans un repère du plan.
On désigne par (In) la suite définie pour tout entier n
supérieur ou égal à 1 par :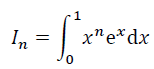
1. a. On désigne
par F1 la fonction définie sur [0 ;1] par :
F1(𝑥)=(x−1)e𝑥.
Vérifier que F1 est une primitive de la fonction f1.
On dérive F1 en posant u = x-1 et v = ex ; u' = 1
; v' = ex ; u'v+v'u = xex = f1(x).
b. Calculer I1.
I1 =
F1(1)-F1(0) =0-(-1) = 1.
2. À l’aide d’une
intégration par parties, établir la relation pour tout n supérieur ou
égal à 1,
In+1=e−(n+1)In.
On pose u = xn+1 et v '= ex ; u' = (n+1) xn
; v' = ex.

3. Calculer I2.
I2=e−(1+1)I1=e-2.
4. On
considère la fonction mystere écrite dans le langage Python :
from math import e # la constante d'Euler e
def mystere(n):
a = 1
L = [a]
for i in range(1,n):
a = e - (i+1)*a
L.append(a)
return L
À l’aide des questions précédentes, expliquer ce que renvoie l’appel
mystere(5).
Cette fonction renvoie la liste des valeurs I1, I2,
I3, I4 et I5.
Partie II
1. Sur le graphique
ci-dessous, on a représenté les courbes C1, C2, C3,
C10, C20 et C30 .

a. Donner une
interprétation graphique de In.
In est la valeur de l'aire comprise entre l'axe des
abscisses, la courbe Cn et les droites d'équation x=0 et x=1.
b. Quelle
conjecture peut-on émettre sur la limite de la suite (In) ?
Cette aire diminue lorsque n augmente.
Conjecture
: la limite
de la suite (In) est nulle.
2. Montrer que
pour tout n supérieur ou égal à 1,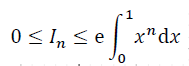
0 < x < 1.
La fonction exponentielle ex étant strictement croissante : e0 < ex < e1.
Multiplier par xn positif : xn e0 < xn ex < xne1 ; xn < xn ex < xne ; 0 < xn ex < xne .

3. En déduire la
limite de In quand n tend vers plus l'infini.
Quand n tend vers plus l'infini, 1 / (n+1) tend vers zéro.
|
|
Exercice 6.
Pour chacune des affirmations suivantes, indiquer si elle est vraie ou
fausse. Chaque réponse doit être justifiée. Une réponse non justifiée
ne rapporte aucun point.
On considère la suite (un) définie : un+1=un
/ (1+2un) pour tout entier naturel n et u0=1
Affirmation 1 :
« u4=1/9 .» Vrai.
u1=u0 / (1+2u0)=1/3.
u2=u1 / (1+2u1)=1/3 / [1+2/3]=1/3 /
[3/3+2/3]=1/5.
u3=u2 / (1+2u2)=1/5 / [1+2/5]=1/3 /
[5/5+2/5]=1/7.
u4=u3 / (1+2u3)=1/7 / [1+2/7]=1/7 /
[7/7+2/7]=1/9.
Affirmation 2 : «
Pour tout entier naturel n, un=1/ (2n+1) . »Vrai.
Initialisation : la
propriété est vraie au rang zéro.
Hérédité :
un=1/ (2n+1) est supposée vraie.
un+1=un / (1+2un)=[1/ (2n+1)] / [1+2 /
(2n+1)] =[1/ (2n+1)] / [(2n+1+2) / (2n+1)] =1/ (2n+3)= 1 /(2n+2+1) = 1
/ [2(n+1)+1].
La propriété est vraie au rang n+1.
Conclusion
: la propriété est vraie au rang zéro et héréditaire, elle est donc
vraie pour tout entier naturel n.
Affirmation 3 : «
La suite numérique (un) est minorée par 10−10.» Faux.
Résoudre un > 10-10.
1/ (2n+1) > 10-10.
Inverser :
1010 < 2n+1 ; n > 0,5x 1010-0,5.
Il existe de nombreuses valeurs de n répondant à cette inégalité.
Exercice 7.
On considère les fonctions fk définies sur R par fk(x))=
x +ke−x, où k est un réel strictement positif.
1. On s’intéresse
dans cette question au cas k = 0,5, donc à la fonction f0,5
définie sur R par
f0,5 (x)= x +0,5e−𝑥.
a. Montrer que la
dérivée de f0,5 notée f '0,5 vérifie f '0,5
(x)= 1−0,5e-x.
f '0,5 (x)= 1+0,5 (-1)e-x= 1−0,5e-x.
b. Montrer que la
fonction f0,5 admet un minimum en ln(0,5).
1−0,5e-x = 0 ; 1 / 0,5 =e-x ; ln(1/0,5) =-
ln(0,5)= -x ; x = ln(0,5) = -ln(2)
Si x < ln(0,5) : e-x > 2 et f '0,5 (x) <
0 et f0,5 (x) est décroissante.
Si x > ln(0,5) : e-x < 2 et f '0,5 (x) >
0 et f0,5 (x) est croissante.
Si x = ln(0,5) : e-x = 2 et f '0,5 (x)= 0 et f0,5
(x) admet un minimum.
Soit k un réel strictement positif. On donne le tableau de variations
de la fonction fk.

2. Montrer que
pour tout réel positif k, fk(lnk)=ln k+1.
fk(ln k)= ln k +ke−ln k=lnk+k / eln k=ln
k +k / k = ln k +1.
On note Ck la courbe représentative de la fonction fk
dans un plan muni d’un repère orthonormé. On note Ak le
point de la courbe Ck d’abscisse lnk.
On a représenté ci-dessous quelques courbes Ck pour
différentes valeurs de k.
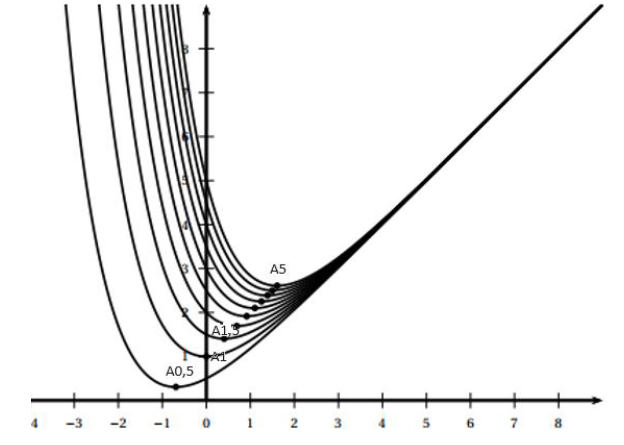
3. Indiquer si
l’affirmation suivante est vraie ou fausse. Justifier la réponse. Une
réponse non justifiée ne rapporte aucun point.
Affirmation : « Pour tout réel k strictement positif, les points
A0,5, A1 et Ak sont alignés. »
Coordonnées des points Ak : ln k ; ln k +1.

L'affirmation est donc vraie.
Exercice 8 :
Pour chacune des affirmations suivantes, indiquer si elle est vraie ou
fausse. Chaque réponse doit être justifiée. Une réponse non justifiée
ne rapporte aucun point.
On considère la suite (un) définie par et u0=0 et
un+1=3un+1
pour tout entier naturel 𝑛.
1. On considère la
fonction calcul écrite dans le langage Python qui
renvoie la valeur de un.
def calcul(n):
u = 0
for i in range(n):
u = 3 * u + 1
return u
On considère par ailleurs la fonction liste écrite dans le langage
Python :
def liste(n):
l = [ ]
for i in range(n):
l.append( calcul(i) )
return l
Affirmation 1
: « l’appel liste(6) renvoie la liste [0, 1, 4, 13, 42,
121]. » Faux.
u0=0 ; u1 = 3x0+1=1 ; u2 = 3x1+1=4 ; u3
= 3x4+1=13 ; u4 = 3x13+1=40 ; u5 =
3x40+1=121.
Affirmation 2
: « pour tout entier naturel n, un=0,5 x3n−0,5 .
» Vrai.
un+1=3un+1=3(0,5 x3n−0,5)+1=0,5 x3n+1-1,5+1=
0,5 x3n+1-0,5.
Affirmation 3
: « pour tout entier naturel n, un+1−un est une
puissance de 3. » Vrai.
un+1−un = 0,5 x3n+1-0,5 -0,5 x3n+0,5=
0,5(3n+1-3n) =0,5x 3n(3-1)=3n.
|
|