QCM,
géométrie,
spécialité mathématiques bac 2024.
.
|
.
.
|
Exercice 4.
On considère le prisme droit ABFEDCGH tel que AB=AD.
Sa base ABFE est un trapèze rectangle en A.
On note I le milieu du segment [EF].
On note J le milieu du segment [AE].

1. On donne les coordonnées de quatre vecteurs dans la base ci-dessus..
Lequel est un vecteur normal au plan (ABG) ?
Vecteurs directeurs du plan (ABG) :
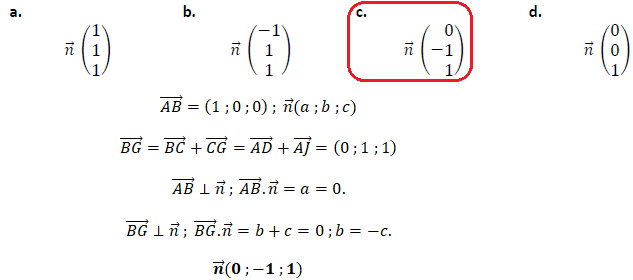
2. Parmi les droites suivantes, laquelle est parallèle à la droite (IJ) ?
a. (DG) vrai ; b. (BD) ; c. (AG) ; d. (FG).
Les droites (IJ) et (AF) sont parallèles. ( droites des milieux dans le triangle AEF).

Les droites (AF) et (DG) sont donc parallèles.
Les droites (IJ) et (DG) sont donc parallèles.
3. Quels vecteurs forment une base de l’espace ?

a. ne convient pas, car il n'y a que deux vecteurs.
b. ne convient pas, car les trois vecteurs sont coplanaires.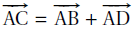
d. ne convient pas, car les trois vecteurs sont coplanaires.
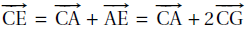
Réponse c.
4. Une décomposition du vecteur AG comme somme de plusieurs vecteurs deux à deux orthogonaux est :
 Réponse b.
Réponse b.
5. Le volume du prisme droit ABFEDCGH, est égal à :
a. 5 / 8 ; b. 8 / 5 ; c. 3 /2 vrai ; d.2.
Soit K le milieu de [DH] ; le prisme est composé du :
cube ABCDJFGK, de volume 1 ;
prisme JFGKHE, qui est la moitié du cube précédent, donc de volume 0,5.
Volume total 1,5 = 3 /2..
|
|
Exercice 5.
1. Sur l’intervalle [0 ; 2p] , l’équation sin(𝑥)=0,1 admet :
a. zéro solution ; b. une solution ; c. deux solutions vrai ; d. quatre solutions.
sin (x ) = 0,1~ sin (0,1) radian.
x ~0,1 radian et x = p-0,1 radian.
2. On considère la fonction f définie sur l’intervalle [0 ;p] par f(x)=x+sin(x). On admet que f est deux fois dérivable.
a. La fonction f est convexe sur l’intervalle [0 ;p]
b. La fonction f est concave sur l’intervalle [0 ;p] vrai.
c. La fonction f admet sur l’intervalle [0 ;p] un unique point d’inflexion
d. La fonction f admet sur l’intervalle [0 ;p] exactement deux points d’inflexion.
f '(x) = 1+cos(x) ; f "(x) = - sin(x).
Sur l’intervalle [0 ;p] la dérivée seconde est négative : la fonction f est concave sur cet intervalle.
3. Une urne
contient cinquante boules numérotées de 1 à 50. On tire successivement
trois boules dans cette urne, sans remise. On appelle « tirage » la
liste non ordonnée des numéros des trois boules tirées. Quel est le
nombre de tirages possibles, sans tenir compte de l’ordre des numéros ?
a. 503 ; b. 1×2×3 ; c. 50×49×48 ; d.50×49×48 / (1×2×3) vrai .
(50 3)=50 x 49 x48 /(1 x2 x3) .
4. On effectue dix
lancers d’une pièce de monnaie. Le résultat d’un lancer est « pile » ou
« face ». On note la liste ordonnée des dix résultats.
Quel est le nombre de listes ordonnées possibles ?
a. 2×10 ; b. 210 vrai ; c. 1×2×3×⋯×10 ; d.1×2×3×⋯×10 / (1×2).
2 résultats sont possibles avec 1 lancer ; 4=22 résultats sont possibles avec 2 lancers ...; 210 résultats sont possibles avec 10 lancers.
5. On effectue n
lancers d’une pièce de monnaie équilibrée. Le résultat d’un lancer est
« pile » ou « face ». On considère la liste ordonnée des n résultats.
Quelle est la probabilité d’obtenir au plus deux fois « pile » dans cette liste ?
a. n(n−1)/2
b. n(n−1)/ 2×0,5n.
c. 1+n+n(n−1)/2.
d. (1+n+n(n−1)/2)×0,5n. Vrai.
Soit X la variable aléatoire donnant le nombre de "pile" sur n lancers. X suit la loi binomiale de paramètres n et 0,5.
P(X<2)=P(X=0) + P(X=1) +P(X=2).
P(X=0)=(n 0) x0,50 x(1-0,5)n-0=0,5n.
P(X=1)=(n 1) x0,51 x(1-0,5)n-1= n 0,5n.
P(X=2)=(n 2) x0,52 x(1-0,5)n-2=n (n-1)/2 x0,5n.
|
|