Sujet 1.
On considère la fonction f définie sur ]0 ; +oo[ par f(x) = x
2 − 8 ln(x), où ln désigne
la fonction logarithme népérien.
On admet que f est dérivable sur ]0 ; +oo[, on note f 'sa fonction dérivée.
1. Déterminer la limite de f(x) quand x tend vers zéro.
x2 tend vers zéro ; ln(x) tend vers moins l'infini ; - ln(x) tend vers plus l'infini.
f(x) tend vers plus l'infini.
.
2. On admet que, pour tout x > 0, f(x) = x
2 (1 − 8
ln(𝑥) x
2 .
En déduire la limite de f(x) en plus l'infini.
x
2 tend vers plus l'infini ; par croissance comparée, ln(x) / x
2 tend vers zéro ; f(x) tend vers plus l'infini.
3. Montrer que, pour tout réel x de ]0 ; +oo[, f '
(x) =
2(x
2−4)/ x
.
f '(x) = 2x -8 / x =( 2x
2-8) / x =
2(x2−4)/ x
.
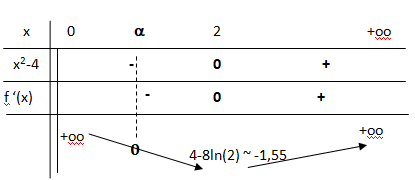
4. Étudier les variations de f sur ]0 ; +∞[ et dresser son tableau de variations
complet.
On précisera la valeur exacte du minimum de f sur ]0 ; +oo[ .
 5.
5. Démontrer que, sur l’intervalle ]0 ; 2], l’équation f(x) = 0 admet une solution
unique
a (on ne cherchera pas à déterminer la valeur de
a).
D'après le tableau de vaariation, l'équation f(x) =0 admet une solution unique sur ]0 ; 2[.
6. On admet que, sur l’intervalle [2 ; +∞[, l’équation f(x) = 0 admet une solution
unique ß (on ne cherchera pas à déterminer la valeur de ß).
En déduire le signe de f sur l’intervalle ]0 ; +oo[.
f(x) >0 sur ]0 ;
a [ et sur ]ß ; +oo[ ; f(x) < 0 sur ]
a ; ß [.
7. Pour tout nombre réel k, on considère la fonction g
k définie sur ]0 ; +oo[ par : g
k(x) = x
2 − 8 ln(x) +k .
En s’aidant du tableau de variations de f, déterminer la plus petite valeur de k
pour laquelle la fonction g
k est positive sur l’intervalle ]0 ; +∞[.
Le minimum de f(x) est égal à 4-8ln(2).
Donc f(x) > 4-8ln(2).
gk(x) =f(x) +k.
4-8ln(2) + k >0 ;
k > 8 ln(2) -4.
La plus petite valeur de k
pour laquelle la fonction gk est positive sur l’intervalle ]0 ; +∞[ est k =8ln(2)-4.