Mathématiques,
probabilités. Bac Métropole 09 / 2023.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Pour
aider à la détection de certaines allergies, on peut procéder à un test
sanguin dont le résultat est positif ou négatif.
Dans une population, ce test donne les résultats suivants :
Si un individu est allergique, le test est positif dans 97 % des cas.
Si un individu
n'est pas allergique, le test est négatif dans 95,7 % des cas.
Par ailleurs, 20 % des individus de cette population présentent un test
positif.
On choisit un individu au hasard et on note :
A l'événement, l'individu est allergique ; on note x = p(A)
T l'événement le test est positif.
Partie A.
1. Compléter
l'arbre ci-dessous.

2.a Démontrer que
p(T) = 0,927x +0,043.
Loi des probabilités totales :
P(T) = 0,97 x + 0,043(1-x) = 0,927x +0,043.
b. En déduire la
probabilité que l'individu soit allergique.
0,927x +0,043 = 0,20.
0,927x = 0,157 ; x =0,157 / 0,927 ~0,169.
3. Justifier par un calcul l'affirmation suivante.
Si le test d'un individu choisi au hasard est positif, il y a plus de 80 % de chances que cet individu soit allergique.
pT(A) =p(A n T) / p(T) = 0,97 x / 0,20 =0,97 x 0,169 / 0,20 ~0,82. ( 82 %). Affirmation vraie.
Partie B.
On réalise une enquète sur les allergies en interrogeant 150 habitants
choisis au hasard, et on admet que ce choix se ramène à des tirages
successifs indépendants avec remise.
On sait que la probabilité qu'un habitant soit allergique est égale à 0,08.
On note X la variable alléatoire qui à un échantillon de 150 habitants
choisis au hasard associe le nombre de personnes allergiques dans cet
échantillon.
1. Quelle est la loi de probabilité suivie par X ? Indiquer ses paramètres.
Le tirages successifs sont indépendants et chaque personne a une probabilité d'être allergique égale à 0,08.
X sui la loi binomiale de paramètre n = 150 et p = 0,08.
2. Déterminer la probabilité que 20 personnes exactement parmi les 150 interrogées soient allergiques.
p(X=20) ~ 0,008 d'après la calculatrice.
3. Déterminer la probabilité qu'au moins 10 % des personnes parmi les 150 interrogées soient allergiques.
p (X < 0,1) = 0,853 5 ; p (X > 0,1) = 1 -0,8535 ~0,147.
|
...
|
....
|
La
paratuberculose est une maladie digestive infectieuse qui touche les
vaches. Elle est due à une bactérie présente dans l'intestin de la
vache.
On réalise une étude dans une région où 0,4 % de la population de vaches est infectée.
On choisit une vache au hasard de cette région. Compte tenu des caractéristiques du test, on sait que :
Si la vache est atteinte par l'infection, la probabilité que le test soit positif est de 0,992.
Si la vache n'est pas atteinte par l'infection, la probabilité que le test soit négatif est de 0,984.
On désigne par :
I : la vache est atteinte par l'infection.
T : le test est positif.
Partie A.
1. Compléter l'arbre suivant.
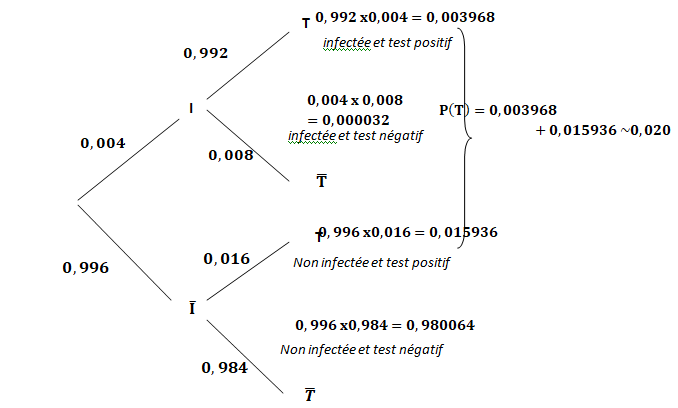
2.a. Calculer la probabilité que la vache ne soit pas atteinte par l'infection et que son test soit négatif.
P(non I n non T) =0,996 x0,984 ~0,980.
b. Montrer que la probabilité que la vache présente un test positif et d'environ 0,020.
Formule des probabilités totale : p(T) =0,003968 +0,015936 ~0,020.
c. La valeur
prédictive positive du test est la probabilité que la vache soit
atteinte par l'infection sachant que son test est positif. Calculer la
valeur prédictive positive de ce test.
pT(I) =p(T n I ) / p(T) =0,003968 / 0,020 ~0,198.
d. Le test donne
une information erronée sur l'atat de santé de la vache lorsque la
vache n'est pas infectée et présente un résultat positif au test ou
lorqsque la vache et infectée et présente un résultat négatif au test.
Calculer la probabilité que ce test donne une information erronée sur
l'état de santé de la vache.
Vache non infectée avec test positif ou vache infectée avec test négatif.
p(non I n T) + p(I n non T) =0,015936 +0,000032 ~0,0160.
Partie B.
3 Lorsqu'on choisit au hasard dans la région un échantillon de 100 vaches, on assimile ce choix à un tirage avec remise.
La probabilité que le test soit positif est égale à 0,02.
On note X la variable aléatoire qui à un échantillon de 100 vaches
choisies au hasard associe le nombre de vaches présentant un test
positif dans cet échantillon.
a. Quelle est la loi de probabilité suivie par X ? Indiquer ses paramètres.
Le
tirages successifs sont indépendants ; deux issues sont posibles
et chaque vache a une probabilité d'être infectée égale à 0,02.
X sui la loi binomiale de paramètre n = 100 et p = 0,02.
b. Déterminer la probabilité que 3 vaches exactement parmi les 100 vaches présentent un test positif.
p(X=3)=(100 3) x0,023 x(1-0,02)100-3 ~0,182.
c. Déterminer la probabilité qu'il y ait au plus 3 vaches parmi les 100 vaches présentant un test positif.
p (X < 3) ~ 0,859 donné par la calculatrice.
4. On choisit un
échantillon de n vaches. On admet que l'on peut assimiler ce choix à
untirage avec remise. Déterminer la valeur minimale de n pour que la
probabilité qu'il y ait, dans l'échantillon, au moins une vache testée
positive, soit supérieur ou égale à 0,99.
1-p(X=0) > 0,99 ; p(X=0) < 0,01.
p(X=0) = (n 0) x 0,020 x(1-0,02)n-0 =0,98n.
0,98n< 0,01.
n ln(0,98) < ln(0,01)
n > ln( 0,01) / ln(0,98) ; n > 228 vaches.
|
|