Mathématiques, fonctions. Bac Métropole 09 / 2023. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... Partie A. On définit sur l’intervalle ]0 ; +∞[ la fonction g par : g(x) =2 / x −1 / x2+ln(x). On admet que la fonction g est dérivable sur ]0 ; +∞[= I et on note g′ sa fonction dérivée. 1. Montrer que pour x >0, le signe de g′(x) est celui du trinôme du second degré (x2−2x +2). g'(x) = -2 /x2+2/ x3 +1/x=(-2x+2+x2)/x3. Sut I x3 >0 ; le signe de g′(x) est donc celui du trinôme du second degré (x2−2x +2). 2. En déduire que la fonction g est strictement croissante sur ]0 ; +∞[. x2−2x +2 = (x-1)2+1. (x-1)2+1 > 1 > 0, le trinôme est positif pour tout x de I. la fonction g est strictement croissante sur I. 3. Montrer que l’équation g(x) = 0 admet une unique solution sur l’intervalle [0,5; 1], que l’on notera a. g(0,5) =4 -4+ln(0,5)=ln(0,5) = -ln(2). g(1)=2-1+0=1. De plus g(x) est strictement croissante sur I, donc d'après le théorème des valeurs intermédiaires, l’équation g(x) = 0 admet une unique solution sur l’intervalle [0,5; 1]. 4. On donne le tableau de signes de g sur l’intervalle ]0 ; +∞[= I : Justifier ce tableau de signes à l’aide des résultats obtenus aux questions précédentes. g(0,5) ~ -0,69 et g(1) = 1. Le théorème des valeurs intermédiaire permet d'affirmer que 0,5 < a < 1. Partie B. On considère la fonction f définie sur l’intervalle ]0 ; +∞[= I par : f (x) = ex ln x. On note Cf la courbe représentative de f dans un repère orthonormé. 1. On admet que la fonction f est deux fois dérivable sur ]0 ; +∞[, on note f ′ sa fonction dérivée, f ′′ sa fonction dérivée seconde et on admet que : pour tout nombre réel x > 0, f ′(x) = ex (1 / x +ln x). Démontrer que, pour tout nombre réel x > 0, on a : f ′′(x) = ex (2 /x −1/x2 +ln x). On pose u = ex et v = (1 / x +ln x). u' = ex ; v' = -1/x2 +1/x . u'v+v'u =ex (1 / x +ln x)+ex (-1/x2 +1/x)=ex(2 /x −1/x2 +ln x). 2. On pourra remarquer que pour tout réel x > 0, f ′′(x) = ex g(x), où g désigne la fonction étudiée dans la partie A. 3. a. Dresser le tableau de signes de la fonction f sur ]0 ; +∞[. Justifier. ex est positif sur I ; le signe de f ''(x) est celui de g(x). b. Justifier que la courbe Cf admet un unique point d’inflexion A. Si f ''(x) s'annule et change de signe, la courbe Cf admet un point d'inflexion. f ′′(x) = ex g(x)=0 entraîne g(x) = 0  entraîne x = a. 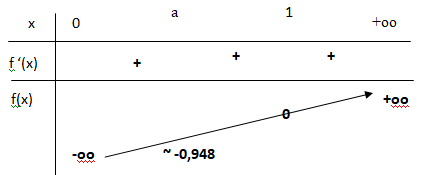A ( a ; f(a) soit A( 0,952 ; -0,948) c. Étudier la convexité de la fonction f sur l’intervalle ]0 ; +∞[. Justifier. Sur l'intervalle ]0 ; a], f ''(x) < 0 et donc f(x) est concave sur cet intervalle. Sur l'intervalle [ a ; +oo[, f ''(x) > 0 et donc f(x) est convexe sur cet intervalle. 4. a. Calculer les limites de f aux bornes de son ensemble de définition. En zéro : ex tend vers 1 et ln(x) tend vers moins l'infini. Par produit des limites, la limite de f(x) en zéro est - oo. En plus l'infini : ex tend vers plus l'infini ; ln(x) tend vers plus l'infini. Par produit des limites, la limite de f(x) en plus l'infini est  + oo. b. Montrer que f ′(a) =ea/a2 (1−a). On rappelle que a est l’unique solution de l’équation g(x) =0. g(a) = 0 = 2 / a −1 / a2+ln(a). ln(a)= -2 / a +1 / a2= 1 / a2 (1-2a). f '(a) =ea (1 / a +ln a) =ea (1 / a +1 / a2 (1-2a)) =ea/a2 (1−a). c. Démontrer que f ′(a) > 0 et en déduire le signe de f ′(x) pour x appartenant à ]0 ; +∞[. ea > 0 ; a2 > 0 ; a ~0,592 < 1 donc (1−a) > 0. Donc f(a) >0. De plus f ''(x) = ex g(x), donc : sur ]0 ; a], g(x) < 0 donc f ''(x <0 ; la fonction f '(x) est décroissante sur cet intervalle. sur ]a  ; +oo [, g(x) > 0 donc f ''(x >0 ; la fonction f '(x) est croissante sur cet intervalle. Donc f '(a) est le minimum de f '(a) sur ]0 ; +oo[. f '(a) > 0 ; f '(x) > 0  et la fonction f(x) est strictement croissante  sur ]0 ; +∞[. d. En déduire le tableau de variations complet de la fonction f sur ]0 ; +∞[. ... .... On considère la fonction f définie sur l’intervalle ]0 ; +∞[ par f (x) = (2−lnx) . ln x, On admet que la fonction f est deux fois dérivable sur ]0 ; +∞[. On note C la courbe représentative de la fonction f dans un repère orthogonal et C′ la courbe représentative de la fonction f ′, fonction dérivée de la fonction f . La courbe C′ est donnée ci-dessous ainsi que son unique tangente horizontale (T). 1. Par lecture graphique, avec la précision que permet le tracé ci-dessus, donner : a. le coefficient directeur de la tangente à C au point d’abscisse 1. f ' (1) ~ 2. b. le plus grand intervalle sur lequel la fonction f est convexe. La fonction f '(x) doit être croissante : [7,4 ; +oo[. 2. a. Calculer la limite de la fonction f en +∞. f (x) = (2−lnx) . lnx. En plus l'infini : ln(x) tend vers plus l'infini ; 2-ln(x) tend vers moins l'infini. Par produit des limites, f(x) tend vers moins l'infini si x tend vers plus l'infini. b. Calculer la limite de la fonction f en zéro. Interpréter graphiquement ce résultat. En zéro : ln(x) tend vers moins l'infini ; 2-ln(x) tend vers plus l'infini. Par produit des limites, f(x) tend vers moins l'infini si x tend vers zéro. La droite d'équation x = 0 est asymptote verticale. 3. Montrer que la courbe C coupe l’axe des abscisses en deux points exactement dont on précisera les coordonnées. On résoud l'équation f(x) = 0 ; (2−lnx) . ln x = 0. ln x =0 soit x = 1 et 2-ln x=0 soit x = e2. Coordonnées de ces points : ( 1 ; 0 ) et (e2 ; 0). 4. a. Montrer que pour tout réel x appartenant à ]0 ; +∞[, f ′(x) =2(1−lnx) / x. f (x) = (2−lnx) . ln x. On pose u = ln x et v = 2 -ln x ; u' = 1 /x ; v' = -1/x. u'v+v' u = (2-ln( x)) / x -ln(x) / x =2 / x ( 1-ln(x)). 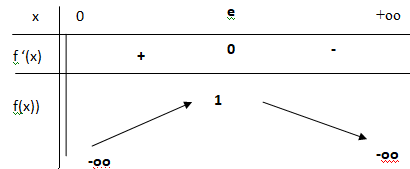b. En déduire, en justifiant, le tableau de variations de la fonction f sur ]0 ; +∞[. 2 / x  >0 ; si x = e, f '(x) = 0. Si x appartient à ]0 ; e], f '(x) >0 et f(x) est croissante. Si x appartient à [e ; +oo[, f '(x) < 0 et f(x) est décroissante. 5. On note f ′′ la dérivée seconde de f et on admet que pour tout réel x appartenant à ]0 ; +∞[, f ′′(x) =2(ln(x) −2)/ x2 . Déterminer par le calcul le plus grand intervalle sur lequel la fonction f est convexe et préciser les coordonnées du point d’inflexion de la courbe C. 2x2 >0 ; le signe de f ''(x) est celui de ln(x) -2. Si x > e2, ln(x) -2 >0 et la fonction f(x) est convexe sur [e2 ; +oo[. f ''(x) = 0 si x = e2 ; f(e2) = 0. Le point de coordonnées ( e2 ; 0) est un point d'inflexion.

menu