QCM, Probabilités, Mathématiques, bac général Amérique du Nord 2023. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... Sujet 1. Uans un souci d’améliorer sa politique en matière de développement durable, une entreprise a réalisé une enquête statistique sur sa production de déchets. Dans cette enquête, les déchets sont classés en trois catégories :  - 69% des déchets sont minéraux et non dangereux ; - 28% des déchets sont non minéraux et non dangereux ; - les déchets restants sont des déchets dangereux. Cette enquête statistique nous apprend également que :  - 73% des déchets minéraux et non dangereux sont recyclables ; - 49% des déchets non minéraux et non dangereux sont recyclables ; - 35% des déchets dangereux sont recyclables. 1. Recopier et compléter l’arbre pondéré ci-dessous représentant la situation de l’énoncé. 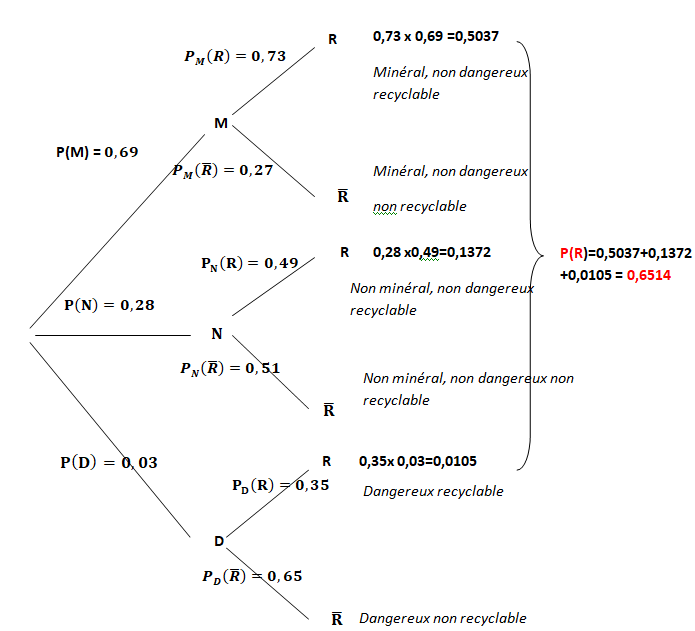2. Justifier que la probabilité que le déchet soit dangereux et recyclable est égale à 0,010 5.  3. Déterminer la probabilité P ( M ∩ non R ) et interpréter la réponse obtenue dans le contexte de l’exercice. P ( M ∩ non R )= 0,69 x0,27 =0,1863. La probabilité qu'un déchet soit minéral, non dangereux, non recyclable est égale à 0,1863.  4. Démontrer que la probabilité de l’évènement R est P(R) = 0,6514.  5. On suppose que le déchet prélevé est recyclable. Déterminer la probabilité que ce déchet soit non minéral et non dangereux. On donnera la valeur arrondie au dix-millième. PR(N) = P(R n  N) / P(R) = 0,1372 / 0,6514=0,2106. Partie B On rappelle que la probabilité qu’un déchet prélevé au hasard soit recyclable est égale à 0,651 4. 1. Afin de contrôler la qualité de la collecte dans l’entreprise, on prélève un échantillon de 20 déchets pris au hasard dans la production. On suppose que le stock est suffisamment important pour assimiler le prélèvement de cet échantillon à un tirage avec remise. On désigne par X la variable aléatoire égale au nombre de déchets recyclables dans cet échantillon.  a. On admet que la variable aléatoire X suit une loi binomiale. Préciser ses paramètres. n = 20 ; p =0,6514.  b. Donner la probabilité que l’échantillon contienne exactement 14 déchets recyclables. On donnera la valeur arrondie au dix-millième. P(X=14)=(2014)x0,651414 x0,34866~0,1723. 2. Dans cette question, on prélève désormais n déchets, où n désigne un entier naturel strictement positif.  a. Donner l’expression en fonction de n de la probabilité pn qu’aucun déchet de cet échantillon ne soit recyclable. Soit Xn la variable aléatoire qui compte le nombre de déchets recyclables  dans cet échantillon. Xn suit la loi binomiale de paramètre (n ; 0,6514). pn =P(Xn=0)=(n0)x0,65140 x0,3486n=0,3486n. b. Déterminer la valeur de l’entier naturel n à partir de laquelle la probabilité qu’au moins un déchet du prélèvement soit recyclable est supérieure ou égale à 0,999 9. 1-pn > 0,999 9 ; -pn > -0,000 1 ; pn < 0,000 1 0,3486n < 0,000 1 ; n ln(0,3486) < ln(0,000 1) -1,054 n < -9,21 ;  n > 9,21 / 1,054 ; n > 8,7 ; n > 9. ... .... Sujet 2. 1. On considère la fonction f définie sur l’intervalle ]1 ; +oo[ par f (x) = 0,05− ln(x) / (x −1) . La limite de la fonction f en +oo est égale à :  a. +oo ;  b. 0,05 vrai ;  c. −oo ; d. 0. f(x) = 0,05 -ln(x) / x * x /(x-1). En plus l'infini : ln(x) / x tend vers zéro. x /(x-1) tend vers 1. Par suite f(x) tend vers 0,05. 2. On considère une fonction h continue sur l’intervalle [−2;4] telle que : h(−1) = 0, h(1) = 4, h(3) = −1. On peut affirmer que : a. la fonction h est croissante sur l’intervalle [−1 ; 1].  b. la fonction h est positive sur l’intervalle [−1 ; 1]. c. il existe au moins un nombre réel a dans l’intervalle [1 ; 3] tel que h(a) = 1. Vrai.  d. l’équation h(x) = 1 admet exactement deux solutions dans l’intervalle [−2 ; 4]. On applique le théorème de la valeur intermédiaire sur [1 ; 3]. 3. On considère deux suites (un) et (vn) à termes strictement positifs telles que la limite de un en plus l'infini soit plus l'infini  et (vn) converge vers 0 . On peut affirmer que : a. la suite (1 /vn) converge.  b. la suite ( vn /un ) converge. Vrai. ( limite du quotient de deux suites) c. la suite (un) est croissante. d. la limite en plus l'infini de (−un) n = −oo. 4. Pour participer à un jeu, un joueur doit payer 4 €. Il lance ensuite un dé équilibré à six faces : - s’il obtient 1, il remporte 12 € ; - s’il obtient un nombre pair, il remporte 3 €;  - sinon, il ne remporte rien.  En moyenne, le joueur :  a. gagne 3,50 €.  b. perd 3 €.  c. perd 1,50 €. d. perd 0,50 €. Vrai. Soit X la variable aléatoite donnant le gain, c'est à dire ce que l'on gagne moins la mise. tirage nombre 1 nombre pair autre gain 12-4=8 3-4=1 0-4= -4 probabilité 1 /6 3 /6 2 /6 E(X) = 8 /6 +(-1)x3 /6 +(-4) x2 /6 = -0,5  ( perte de 0,5 €). 5. On considère la variable aléatoire X suivant la loi binomiale B(3 ; p). On sait que P(X = 0) = 1/ 125 . On peut affirmer que : a. p = 1 /5 ; b. P(X = 1) = 124 /125 ; c. p = 4 /5 vrai ; d. P(X = 1) = 4/ 5. p(X=0) = (3 0)  x p0 x(1-p)3-0 = (1-p)3 = 1 / 125 =(1 / 5)3. 1-p = 1 /5 ; p = 4 / 5.

menu