On
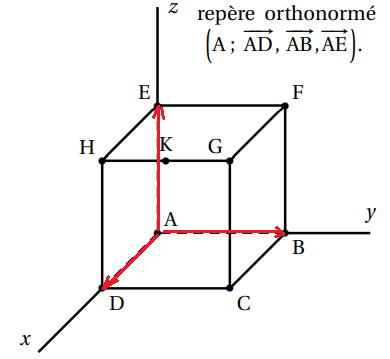
considère le cube ABCDEFGH d’arête
1 représenté ci-dessous.
On note K le milieu du segment [HG].
 1.
1. Justifier que les points C, F et K définissent un plan.
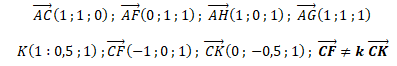
Ces deux vecteurs n'étant pas colinéaires, les points C, F et K définissent un plan.
2. a. Donner, sans justifier, les longueurs KG, GF et GC.
KG = 0,5 ; GF = 1 ; GC = 1.
b. Calculer l’aire du triangle FGC.
Triangle rectangle en G ( moitié du carré BCFG) : GF x CG / 2 = 1 x 1 /2 = 0,5 unité d'aire.
c. Calculer le volume du tétraèdre FGCK.
Base CFG x hauteur GK / 3 = 0,5 x 0,5 / 3 = 1 / 12 unité de volume.
3. a. On note n le vecteur de coordonnées (1 ; 2 , 1).
Démontrer que n est normal au plan (CFK).
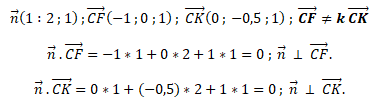
Le vecteur n est orthogonal à deux vecteurs non colinéaires du plan (CFK), donc c'est un vecteur orthogonal à ce plan.
b. En déduire qu’une équation cartésienne du plan (CFK) est :
x +2y + z −3 = 0.
x+2y+z+d=0.
C(1 ; 1 ; 0) appartient à ce plan :1 +2 +0+d = 0 ; d = -3.
4. On note
D la droite passant par le point G et orthogonale au plan (CFK).
Démontrer qu’une représentation paramétrique de la droite
D est :
x = 1+ t
; y = 1+2t
; z = 1+ t avec t réel.
Le vecteur n (1 ; 2 ; 1) est un vecteur directeur de cette droite
D.
x = t+x
G =t+1 ; y = 2t+y
G = 2t+1 ; z = t +z
G = t+1.
5. Soit L le point d’intersection entre la droite
D et le plan (CFK).
a. Déterminer les coordonnées du point L.
L appartient au plan (CFK) et à la droite D :
1+t +2(2t+1) +1+t-3 = 0 ; 6t +1=0 ; t = -1 /6.
L( 5 /6 ; 4 /6 ; 5 /6).
b. En déduire que LG = 6
½ /
6.
LG = [(1-5 /6)
2 +(1-4 /6)
2 +
(1-5 /6)2 ] ½= (12 +22+12)½ / 6= 6½ /
6.
6. En utilisant la question 2., déterminer la valeur exacte de l’aire du triangle CFK.
Le tétraèdre FGCK a pour base le triangle CFK et pour hauteur LG.
Son volume vaut : aire triangle CFK x LG / 3 =1 / 12.
Aire triangle CFK x 6½ /
(6 x3) = 1 /12.
Aire triangle CFK x 6½ / 3 = 1 /2.
Aire triangle CFK =3 / (2 x6½ )=6½ / 4.