Probabilités, bac Nlle Calédonie 2023.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

.
. . .

.
.
.. ..
......


...
Une entreprise de location de bateaux de tourisme propose à ses clients deux types de bateaux : bateau à voile et bateau à moteur. Par ailleurs, un client peut prendre l’option PILOTE. Dans ce cas, le bateau, qu’il soit à voile ou à moteur, est loué avec un pilote. On sait que :
 • 60 % des clients choisissent un bateau à voile ; parmi eux, 20 % prennent l’option PILOTE.
• 42 % des clients prennent l’option PILOTE.
On choisit au hasard un client et on considère les évènements :
• V : « le client choisit un bateau à voile »; • L : « le client prend l’option PILOTE ».
Partie A
1. Traduire la situation par un arbre pondéré que l’on complètera au fur et à mesure.

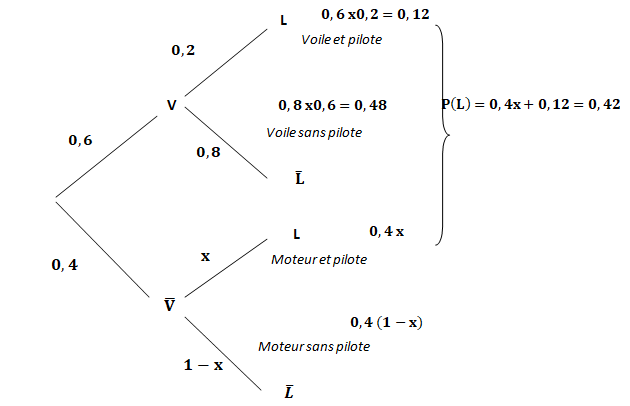 2. Calculer la probabilité que le client choisisse un bateau à voile et qu’il ne prenne pas l’option PILOTE.
P(V n non L) =0,8 x0,6 = 0,48.
3. Démontrer que la probabilité que le client choisisse un bateau à moteur et qu’il prenne l’option PILOTE est égale à 0,30.
0,4x +0,12 = 0,42 ; 0,4x = 0,30.
4. En déduire PnonV (L), probabilité de L sachant que V n’est pas réalisé.
PnonV (L) = P(L n nonV) / P(non V) =0,30 / 0,40 =0,75.
 5. Un client a pris l’option PILOTE. Quelle est la probabilité qu’il ait choisi un bateau à voile ? Arrondir à 0,01 près.
PL(V) = P(L n V) / P(L) =0,12 / 0,42 ~0,29.
Partie B
Lorsqu’un client ne prend pas l’option PILOTE, la probabilité que son bateau subisse une avarie est égale à 0,12. Cette probabilité n’est que de 0,005 si le client prend l’option PILOTE.
On considère un client. On note A l’évènement : « son bateau subit une avarie ».
1. Déterminer P(L ∩ A) et P( non L ∩ A ) .
P(L ∩ A) =0,42 x 0,005 =0,002 1.
 P( non L ∩ A ) =0,58 x0,12=0,069 6.
2. L’entreprise loue 1 000 bateaux. À combien d’avaries peut-elle s’attendre ?
P(L ∩ A) + P( non L ∩ A ) =0,002 1 +0,069 6=0,071 7.
Nomnre de bateaux subissant une avarie : 0,0071 7 x1000 ~ 72.

Partie C
On rappelle que la probabilité qu’un client donné prenne l’option PILOTE est égale à 0,42. On considère un échantillon aléatoire de 40 clients. On note X la variable aléatoire comptant le nombre de clients de l’échantillon prenant l’option PILOTE. 1. On admet que la variable aléatoire X suit une loi binomiale. Donner sans justification ses paramètres.
Paramètres : n = 40 ; p = 0,42.
2. Calculer la probabilité, arrondie à 10−3 , qu’au moins 15 clients prennent l’option PILOTE.
p(X > 15) = 1 -p(X < 14)=0,768.

...
....

 QCM
L’énoncé ci-dessous est commun aux questions 1. et 2. Les 200 adhérents d’un club sont des filles ou des garçons. Ces adhérents pratiquent l’aviron ou le basket selon la répartition figurant dans le tableau ci-dessous.

 Aviron
 Basket
 Total
Filles
 25
 80
 105
Garçons
 50
 45
 95
Total
 75
 125
 200
On choisit un adhérent au hasard et on considère les évènements suivants :
 F : l’adhérent est une fille ; A : l’adhérent pratique l’aviron.
 1. La probabilité de F sachant A est égale à :
a. 25 /100  ; b. 25/ 75 vrai; c. 25 /105 ; d. 75 / 105
PA(F) =P(A n F) / P(A) = 25 / 75.
2. La probabilité de l’évènement A u F est égale à :
a. 9/ 10 ; b. 1/ 8 ;c. 31/ 40 vrai ; d. 5 /36.
P(A u F) = P(A) + P(F) - P(A n F) =75 / 200 + 105 / 200 - 25 / 200 =155 / 200 = 31 / 40.
L’énoncé ci-dessous est commun aux questions 3. et 4. Pour se rendre à son travail, Albert peut utiliser au choix le bus ou le train.
La probabilité que le bus soit en panne est égale à b.
La probabilité que le train soit en panne est égale à t.
 Les pannes de bus et de train surviennent de façon indépendante.
 3. La probabilité p1 que le bus ou le train soient en panne est égale à :
 a. p1 = b t ; b. p1 = 1−b t ; c. p1 = b + t ; d. p1 = b + t −b t. Vrai.
On appelle  : B : " le bus est en panne" ; T : " le train est en panne".
P(B n T) = P(B) x P(T) = bt.
p1 = P(B u T) = P(B) + P(T) - P(B n T) = b + t -bt.

 4. La probabilité p2 que Albert puisse se rendre à son travail est égale à :
 a. p2 = b t ; b. p2 = 1−b t vrai ; c. p2 = b + t d. ; p2 = b + t −b t.
Il ne faut pas que le train ou le bus soit en panne en même temps. On cherche la probabilité contraire à B n T.
p2 = 1-bt.

 5. On considère une pièce de monnaie pour laquelle la probabilité d’obtenir FACE est égale à x. On lance la pièce n fois. Les lancers sont indépendants. La probabilité p d’obtenir au moins une fois FACE sur les n lancers est égale à a.
 p = x n ; b. p = (1− x) n;  c. p = 1− x n ; d. p = 1−(1− x) n. Vrai.
Probabilité d'obtenir que des PILE : (1-x)n.
Probabilité d'obtenir au moins une fois FACE : 1-(1-x)n.

  
menu