On considère la fonction f définie pour tout réel x de l’intervalle ]0 ; +∞[ par :
f (x) = 5x
2 +2x −2x
2
ln(x).
On note C
f
la courbe représentative de f dans un repère orthogonal du plan.
On admet que f est deux fois dérivable sur l’intervalle ]0 ; +∞[.
On note f
′
sa dérivée et f
′′ sa dérivée seconde.
1. a. Démontrer que la limite de la fonction f en 0 est égale à 0.
La limite en 0
+ de
5x
2 +2x est égale à 0.
La limite en 0+ de 2x2ln(x) est égale à zéro par croissance comparée.
Par somme des limites, la limite de f(x) en 0+ est égale à 0.
b. Déterminer la limite de la fonction f en +∞.
f(x) = x
2 [5+2/x-2 ln(x)].
En +oo : 2 /x tend vers zéro.
5+2/x tend vers 5.
ln(x) tend vers +oo et -ln(x) tend vers-oo.
Par somme des limites, f(x) tend vers -oo.
2. Déterminer f
′
(x) pour tout réel x de l’intervalle ]0 ; +∞[.
Calcul de la dérivée de 2x
2 ln(x) en posant u = 2x
2 et v = ln(x) ; u' = 4x ; v' = 1/x.
u'v+v'u = 4x ln(x) +2x.
f '(x) = 10x+2-4x ln(x) -2x=
8x +2 -4x ln(x).
3. a. Démontrer que pour tout réel x de l’intervalle ]0 ; +∞[
f
′′(x) = 4(1−ln(x)).
On dérive 4x ln(x) en posant u = 4x et v = ln(x) ; u' = 4 et v' =1/x.
u'v+v'u = 4 ln(x)+4.
f "(x)=8-4 ln(x)-4=4(1-ln(x)).
b. En déduire le plus grand intervalle sur lequel la courbe C
f est au-dessus de ses
tangentes.
La courbe C
f est au dessus de ces tangentes si et seulement si f est convexe, c'est à dire si f "(x)
>0.
1-ln(x)
>0 ; ln(x)
< 1 ; x
< e.
L'intervalle recherché est : ]0 ; e].
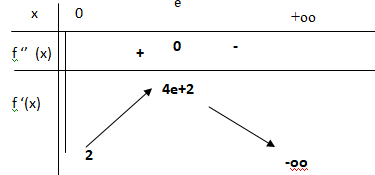
c. Dresser le tableau des variations de la fonction f
′
sur l’intervalle ]0 ; +∞[.
(On admettra que
f
′
(x) = 2 quand x tend vers 0
+ et que f
′
(x) tend vers moins l'infini quand x tend vers +oo ).
 4. a.
4. a. Montrer que l’équation f
′
(x) = 0 admet dans l’intervalle ]0 ; +∞[ une unique
solution
a dont on donnera un encadrement d’amplitude 10
−2
.
Sur l'intervalle ]0 ; e], f '(x) est strictement croissante et de plus f '(x) > 2.
Sur l'intervalle [e ; +oo], f '(x) est strictement décroissante de 4e+2 à -oo.
f '(x) est continue car dérivable.
D'après le corollaire du théorème des valeurs intermédiaire, l'équation f '(x) = 0 adment une unique solution a sur [e ; +oo[.
7,87 < a < 7,88.
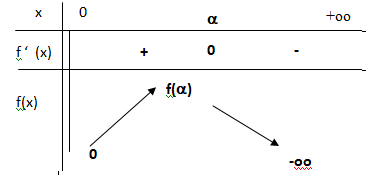
b. En déduire le signe de f
′
(x) sur l’intervalle ]0 ; +∞[ ainsi que le tableau des variations de la fonction f sur l’intervalle ]0 ; +∞[.
 5. a.
5. a. En utilisant l’égalité f
′
(
a) = 0, démontrer que :
ln(
a) =
(4
a+1)/
(2
a)
.
En déduire que f (
a) =
a
2 +
a.
f ''(
a)=8
a+2-4
a ln(
a).
f '(
a) =0 conduit à
8 a+2-4a ln(a)=0.
4a ln(a)=8 a+2.
ln(a) =
(4a+1)/
(2a).
f(a)=5 a2+2a-2a2ln(a)= 5 a2+2a-2a2 x
(4a+1)/
(2a).
f(a)= 5 a2+2a-a x
(4a+1) = 4 a2+a.
b. En déduire un encadrement d’amplitude 10
−1 du maximum de la fonction f .
7,87 < a < 7,88.
61,936 9 < a2 < 62,094 4.
69,806 9 < a2 + a < 69,974 4.
69,806 9 < f(a) < 69,974 4.