Question 1
Simplifier l’écriture de l’expression suivante :
A(x) = −ln(9) + 2 ln(3x).
A(x) = - ln(3
2) + ln((3x)
2) =ln [(3x / 3)
2]=
ln(x
2) = 2 ln(x).
Question 2.
Le plan complexe est rapporté à un repère orthonormé.
Le point M d’affixe z
M vérifie les conditions suivantes :
M appartient au cercle de centre O et de rayon 6 ;
la partie réelle de z
M est négative ;
la partie imaginaire de z
M est égale à 3.
1. Soit
q la mesure dans [0 ; 2
p[ de l’argument du nombre
complexe z
M.
Déterminer sin(
q).
Module de z
M = 6. ; sin
q = 3 /6 =0,5.
2. À l’aide du
demi-cercle trigonométrique ci-dessous, donner la valeur exacte de
q.
Justifier.
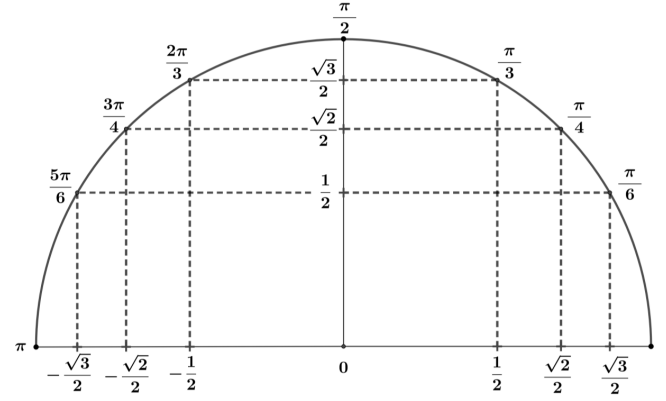
La partie réelle de z
M étant négative et
sin q = 0,5 :
q = 5
p /6.
3. En déduire
l’écriture exponentielle de z
M.
zM =
6 exp ( 5p i / 6).
Question 3
Soit 𝑓 la fonction définie sur R par f(x)) = e
0,01x − 2.
On admet que la fonction f est croissante sur R.
1. On cherche à
déterminer le plus petit entier naturel N qui vérifie f(N) > 98.
Recopier et compléter la ligne 4 de l’algorithme ci-dessous écrit en
langage Python
afin que celui-ci détermine la valeur de N.
from math import*
def seuil();
n=0; y=-1
while
y <= 98 :
n=n+1
y = exp(0,01*n)-2
return n
2. Résoudre
algébriquement dans R l’inéquation f(x) > 98.
exp(0,01x) -2 > 98 ; exp(0,01 x) > 100 ; 0,01 x > ln(100).
x > ln(100) / 0,01 ; x > 100 ln(100).
Question 4
On injecte dans la circulation sanguine d’un patient une solution
contenant un marqueur
afin de réaliser une exploration de la thyroïde.
La concentration dans le sang en µg ∙ mL
−1
, après injection, est modélisée par la fonction f définie sur [0 ; +∞[
par f(t) = 7,88t
2e
−0,75t
, où t est le temps exprimé en heure.
On admet que la fonction f est dérivable sur [0 ; +∞[ et que sa dérivée
f
′ vérifie : f '(t) = t(−5,91t + 15,76)e
−0,75t
.
1. Dresser le
tableau de variations de la fonction f. On ne demande pas la limite en
+∞.
t exp(-0,75 ) étant positif, le signe de la dérivée est celui de -5,91
t +15,76.
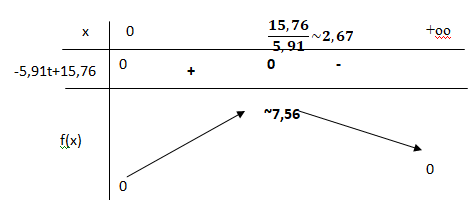 2.
2. L’examen doit être
effectué lorsque la concentration dans le sang du marqueur est
maximale. Justifier que l’examen doit être réalisé entre 2 et 3 heures
après
l’injection.
Le maximum se situe à t ~2,67, valeur appartenant à [2 ; 3 ].