Fonctions,
Bac Amérique du sud 2023.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Partie
A
On considère la fonction f définie sur l’ensemble ]0 ; +∞[ par f (x) = 1+x2 −2x2 ln(x).
On admet que f est dérivable sur l’intervalle et on note f ′ sa
fonction dérivée
1. Justifier que la limite en zéro est 1 et que la limite en plus l'infini est moins l'infini.
f(x) = 1 + x2(1-2ln(x)).
en zéro : x2 = 0 et ln(x) tend vers -oo ; 1-2ln(x) tend vers +oo ; par produit des limites f(x) tend vers 1.
En +oo : -2ln(x) tend vers -oo ; x2 tend vers +oo ; par produit des limites f(x) tend vers -oo.
2. Montrer que pour tout réel x de l’intervalle ]0 ; +∞[, f ′(x) =−4x
ln(x).
On dérive x2(1-2ln(x)) en posant u = x2 ; v = 1-2ln(x) ; u' = 2x ; v' = -2 / x.
u'v+v'u = 2x(1-2ln(x))-2x=-4 x ln(x).
3. Étudier le signe de f ′(x) sur l’intervalle ]0 ; +∞[, puis dresser
le tableau de variation de la fonction sur l’intervalle ]0 ; +∞[.
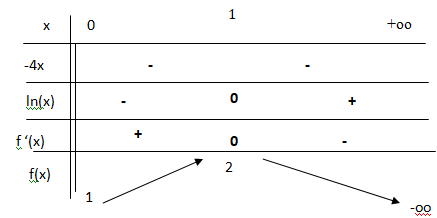
4. Démontrer que l’équation f (x) = 0 admet une unique solution a dans
l’intervalle [1 ; +∞[ et que a appartient à [1 ; e].
f(x) est continue car dérivable sur [1 ; +∞[ et décroissante de 2 à -oo. D'après le théorème des valeurs intermédiaires, il existe un réel unique de [1 ; +∞[ tel que f(a) =0.
Or f(e) =1+e2(1-2ln(e)) =1+e2(1-2) =1-e2 ~-6,4.
D'après ce même théorème, a appartient à [1 ; e].
On admet dans la suite de l’exercice, que l’équation f (x) = 0 n’admet
pas de solution sur l’intervalle ]0; 1].
5. On donne la fonction ci-dessous écrit en Python. L’instruction
fromlycee import * permet d’accéder à la fonction ln.

Il écrit dans la console d’exécution :
>>> dichotomie(1)
Parmi les quatre propositions ci-dessous, recopier celle affichée par l’instruction précédente ?
Justifier votre réponse (on pourra procéder par élimination).
Proposition A : (1.75, 1.9031250000000002)
Proposition B : (1.85, 1.9031250000000002)
Proposition C : (2.75, 2.9031250000000002)
Proposition D : (2.85, 2.9031250000000002).
e ~2,7 ; on part de l’intervalle [1; 2,7], dichotomie(1) donne par dichotomie un encadrement de a par deux réels a et b tels que b −a < 0,1..
Or a ~ 1,9, C et D sont exclus ; A ne donne pas un encadrement au dixième :
La proposition B est retenue.
Partie B
On considère la fonction g définie sur l’intervalle ]0 ; +∞[, par g(x) =ln(x) / (1+x2).
On admet que g est dérivable sur l’intervalle ]0 ; +∞[ et on note g′ sa fonction dérivée.
On note Cg la courbe représentative de la fonction g dans le plan rapporté à un repère orthonormé.
1. Démontrer que pour tout réel x de l’intervalle ]0 ; +∞[, g′(x) = f (x) / [x (1+x2)2] .
On pose u = ln(x) ; v = 1+x2 ; u' = 1 /x ; v' = 2x.
(u'v-v'u) / v2 =[(1+x2) / x -2x ln(x)] / (1+x2)2.
g'(x) =[(1+x2 -2x2 ln(x)/ x] / (1+x2)2= f (x) / [x (1+x2)2] .
2. Démontrer que la fonction g admet un maximum en x = a.
Le dénominateur [x (1+x2)2] est positif ; g'(x) a le signe de f(x).
g'(x) >0 sur ]0 , a] et g(x) est croissante.
g'(x) <0 sur [ a ; +oo[ et g(x) est décroissante.
La fonction g admet un maximum en x = a.
On admet que g(a) =1/ (2a2).
3. On note T1 la tangente à Cg au point d’abscisse 1 et on note Ta la tangente à Cg au point d’abscisse a.
Déterminer, en fonction de a, les coordonnées du point d’intersection des droites T1 et Ta.
Au point d’abscisse a, g(x) a un maximum : la tangente Ta est horizontale d'équation y = 1/ (2a2).
Equation de T1 : y-g(1) =g'(1) (x-1).
y-0=0,5(x-1) ; y =0,5(x-1).
A l'intersection de ces deux droites : 1/ (2a2) =0,5 x-0,5 ; x = 1+1/a2 ; y = 1/ (2a2).
|
...
|
....
|
Soit la fonction f définie sur R par f (x) = ln(1+e−x )+0,25x.
On note Cf la courbe représentative de la fonction f dans un repère orthonormé du plan.
Partie A
1. Déterminer la limite de f en +∞.
En +oo : e-x tend vers zéro ; 1+e-x tend vers 1 et ln(1+e−x ) tend vers zéro.
0,25 x tend vers +oo ; f(x) tend vers +oo.
2. On admet que la fonction f est dérivable sur R et on note f ′ sa fonction dérivée.
a. Montrer que, pour tout réel x, f ′(x) =(e x −3) / [4(e x +1)].
f '(x) = -e-x / (1+e−x ) +0,25 =[ -e-x+0,25(1+e−x )] / (1+e−x ) =( 0,25-0,75 e-x) / (1+e−x ) =(1-3e-x) / (4(1+e−x )).
Multiplier numérateur et dénominateur par ex : f ′(x) =(e x −3) / [4(e x +1)]..
b. En déduire les variations de la fonction f sur R.
[4(e x +1)] >0 ; f '(x) a le signe de ex-3.
x < ln(3) : f '(x) < 0 et f(x) est décroissante.
x > ln(3) : f '(x) >0 et f(x) est croissante.
x = ln(3), f(x) présente un minimum.
c. Montrer que l’équation f (x) = 1 admet une unique solution a dans l’intervalle [2; 5].
ln(3) ~1,1 ; [2; 5] est inclu dans [ln(3) ; +oo[, intervalle dans lequel f est strictement croissante.
f(2)=ln(1+e-2) +0,5 ~0,63 < 1.
f(5) =ln(1+e-5) +1,25 ~6,3 > 1.
f(x) est continue car dérivable sur [l2 ; 5] et strictement croissante de 0,63 à 6,3. D'après le théorème des valeurs intermédiaires, il existe un réel unique de [1 ; +∞[ tel que f(a) =1.
Partie B
On admettra que la fonction f ′ est dérivable sur R et pour tout réel x, f ′′(x) =e x / (e x +1)2 .
On note D la tangente à la courbe Cf au point d’abscisse 0.
Dans le graphique ci-dessous, on a représenté la courbe Cf la tangente D et le quadrilatère MNPQ tel que M et N sont les deux points de la courbe Cf d’abscisses respectives a et −a, et Q et P sont les deux points de la droite D d’abscisses respectives a et −a.
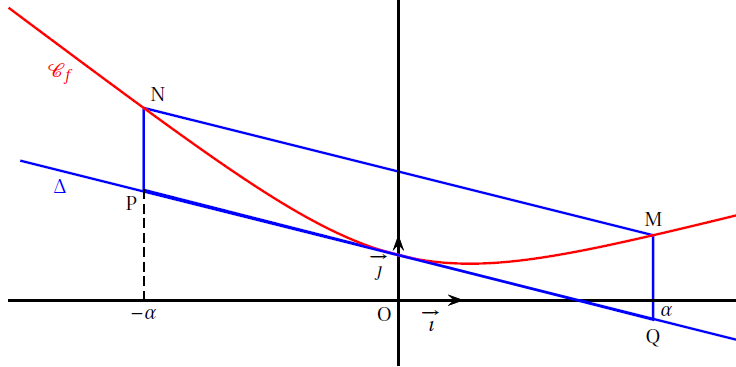
1. a. Justifier le signe de f ′′(x) pour x appartenant à R.
e x > 0 ; (e x +1)2 > 0 ; f "(x) > 0.
b. En déduire que la portion de la courbe Cf sur l’intervalle [−a ; a], est inscrite dans le quadrilatère MNPQ.
f "(x) >0, la fonction f(x) est convexe ; sa courbe
représentative est située au dessus de toutes ces tangentes, donc au
dessus de D.
De plus, entre les points M et N, Cf est située en dessous de la sécante [MN].
Donc la portion de la courbe Cf sur l’intervalle [−a ; a], est inscrite dans le quadrilatère MNPQ.
2. a. Montrer que f (−a) = ln(e-a+1)+0,75 a .
f (−a) = ln(1+ea )-0,25a =ln[ea(e-a+1)]-0,25a =a +ln(e-a+1)-0,25a = ln(e-a+1)+0,75 a .
b. Démontrer que le quadrilatère MNPQ est un parallélogramme.
f(a) = 1 soit ln(1+e−a )+0,25a =1 ; ln(1+e−a )=1-0,25a.
De plus f (−a) = ln(e-a+1)+0,75 a =1-0,25a+0,75 a =1+0,5 a.
M( a ; f(a) ) ; M( a ;1-0,25a );
N(- a ; f(-a) ) ; N( -a ;1+0,75a );
coefficient directeur de la droite (MN) : (yM-yN) / (xM-xN) =[ f(a)-f(-a)] / (2a)= -0,75 a / (2a)= -0,375 = -3 / 8.
Coefficient directeur de la droite D tangente à la courbe Cf au point d’abscisse 0 : f '(0)=(e 0 −3) / [4(e 0 +1)]= -3 /8
La droite D et la droite (MN) sont donc parallèles.
Par construction les droites (MQ) et (NP) sont parallèles.
Le quadrilatère MNPQ est un parallélogramme.
|
|