Géométrie,
Bac Amérique du sud 2023.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Dans l’espace muni d’un repère orthonormé, on considère les points
A(0; 4; 16), B(0 ; 4 ; −10), C(4 ; −8 ; 0) et K(0; 4; 3).
On définit la sphère S de centre K et de rayon 13 comme l’ensemble des points M tels que
KM= 13.
1. a. Vérifier que le point C appartient à la sphère S.
KC =((4-0)2+(-8-4)2+(0-3)2]½ =(16+144+9)½ =169½ = 13.
Donc C appartient à la sphère.
b. Montrer que le triangle ABC est rectangle en C.
AC2 =(4-0)2 +(-8-4)2 +(0-16)2=416.
BC2 =(4-0)2 +(-8-4)2 +(0+10)2=260.
AB2 =(0-0)2 +(4-4)2 +(-10-16)2=676.
AB2 =BC2 +AC2.
D'après la réciproque du théorème de Pythagore, le triangle ABC est rectangle en C.
2. a. Montrer que le vecteur n de coordonnées (3 ; 1 ; 0) est un vecteur normal au plan (ABC).
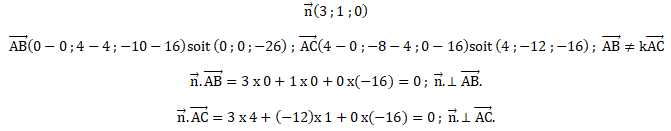
b. Déterminer une équation cartésienne du plan (ABC).
3x+y+d=0.
A appartient à ce plan : xA+yA+d = 0 ; 0+4+d=0 ; d = -4.
3x+y-4=0.
3.
On admet que la sphère S coupe l’axe des abscisses en deux points, l’un
ayant une abscisse positive et l’autre une abscisse négative.
On note D celui qui a une abscisse positive.
a. Montrer que le point D a pour coordonnées (12; 0; 0)
D appartient à l'axe des abscisses : D(x ; 0 ; 0).
D appartient à la sphère : KD =((x-0)2+(0-4)2+(0-3)2]½ =(x2+16+9)½ =169½ ;
x2+25 = 169 ; x=12.
b. Donner une représentation paramétrique de la droite D passant par D et perpendiculaire au plan (ABC).
Le vecteur n (3 ; 1 ;0) est un vecteur directeur de cette droite.
x = 3 k+ xD =3 k +12 ; y =k+yD = k ; z = zD =0 avec k réel.
c. Déterminer la distance du point D au plan (ABC).
Soit I le projeté orthogonal de D sur le plan ABC.
3xI+yI-4=0 et xI=3k+12 ; yI =k ; zI =0.
9k+36+k-4=0 ; 10 k+32 = 0 ; k = -3,2.
xI = 2,4 ; yI = -3,2 ; zI =0.
DI =((2,4-12)2+(-3,2-0)2+(0-0)2]½ =(92,16+10,24)½ =102,4½ = (512 /5)½=24 x (2/ 5)½.
4. Calculer une valeur approchée, à l’unité de volume près, du volume du tétraèdre ABCD.
Base : triangle ABC rectangle en C.
Aire de ce triangle : AC x BC / 2 =(416 x260)½ / 2 ~164,44.
Hauteur DI ~10,12.
Volume = base x hauteur / 3 ~164,44 x10,12 / 3 ~555 unités de volume.
|
...
|
....
|
Dans un repère orthonormé on considère les points :
A(1 ; 1 ; −4), B(2 ; −1 ; −3), C(0 ; −1 ; −1) et W(1; 1; 2).
1. Démontrer que les points A, B et C définissent un plan.
2. a. Démontrer que le vecteur n de coordonnées (1 ; 1 ; 1) est normal au plan (ABC).
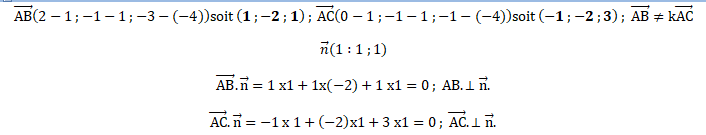
b. Justifier qu’une équation cartésienne du plan (ABC) est x + y +z +2 = 0.
x+y+z+d =0.
A(1 ; 1 -4) appartient à ce plan : 1+1-4+d = 0 ; d = 2.
3. a. Justifier que le point W n’appartient pas au plan (ABC).
xW+yW+zW+2 =1+1+2+2=4 diffère de zéro.
b. Déterminer les coordonnées du point H, projeté orthogonal du point W sur le plan (ABC).
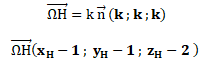
xH =k+1 ; yH = k+1 ; zH =k+2.
H appartient au plan ABC : xH+yH+zH +2 =0.
k+1+k+1+k+2+2=0 ; 3k +6 =0 ; K =-2.
H(-1 ; -1 ; 0).
On admet que WH=2*3½.
On définit la sphère S de centre W et de rayon 2*3½ comme l’ensemble de tous les points M de l’espace tels que WM= 2*3½.
4. Justifier, sans calcul, que tout point N du plan (ABC), distinct de H, n’appartient pas à la sphère S.
H est le projeté orthogonal de W sur le plan (ABC), donc HW est la plus petite distance entre W et tout point du plan.
Tout point M de ce plan autre que H est tel que WM > WH ; WM >2*3½.
M n'appartient pas à la sphère.
On dit qu’un plan P est tangent à la sphère S en un point K lorsque les deux conditions suivantes sont vérifiées :
• K ∈P ∩S
• (WK)⊥P
5. Soit le plan P d’équation cartésienne x + y − z −6 = 0 et le point K de coordonnées K(3; 3; 0).
Démontrer que le plan P est tangent à la sphère S au point K.
xK+yK+zK+2 =3+3-0-6 =0, donc K appartient au plan P.
WK2 = (3-1)2 +(3-1)2 +(0-2)2 = 12 ; WK = 2 *3½ ; donc K appartient àla sphère.
La condition K ∈P ∩S est vérifiée.
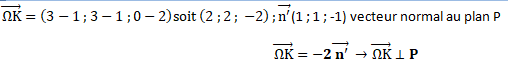
6. On admet que les plans (ABC) et P sont sécants selon une droite (D).
Déterminer une équation paramétrique de la droite (D).
Le vecteur n (1 ; 1 ; 1) est un vecteur normal au plan ABC.
Le vecteur n'(1 ; 1 ; -1) est un vecteur normal au plan P.
Ces vecteurs n'étant pas colinéaires, les plans ABC et P sont donc sécants selon la droite (D).
M(x ; y ; z) appartient à (D) :
x+y+z+2 =0 et x+y-z-6=0.
2z +8=0 ; z = -4.
x+y-2 =0 soit x =2-y.
Représentation paramétrique de la droite (D) :
x = 2-t ; y = t ; z = -4 avec t réel.
|
|