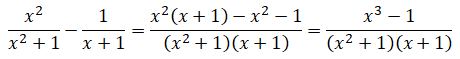
Mathématiques, calcul algébrique, test scientifique avancé tsecia 2023. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... Calcul algébrique et analyse  M1 Pour tout choix du nombre réel x différent de −1, la quantité x2 /(x2+1) - 1/(x+1) est égale à : Réponse E. M2. 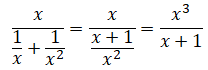Pour tout choix du nombre réel x différent de 0 et de −1, la quantité suivante est égale à : Réponse B.   M3 Pour tout choix du nombre réel x différent de 0, 1 et −1, la quantité suivante est égale à : 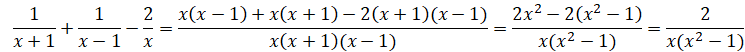Réponse A   M4 L’équation 1/x2 =5x  d’inconnue réelle x admet comme solution : 1/x2 > 0, donc 5x >0, ce qui exclu les valeurs négatives. 5 x3=1 ; x3=1/5=0,2 ; x =+(0,2)1/3. Réponse C.   M5. L'équation 1 / (x+1) = 3 /(x-1) a pour ensemble de solutions : x-1 =3(x+1) ; x-1 = 3x+3 ; 2x=-4 ; x=-2. Réponse B.   M6. L’équation 2x2 − x +1 /9=0 a pour solutions : Discriminant D = (-1)2 -4*2 /9 =1-8/9 = 1/9 =1/32. Solutions x = (1±1/3) / 4 soit { 1/3 ; 1/ 6 } réponse B. M7 L’inéquation x3 > 8 a pour ensemble de solutions : x est positif ; x > 81/3 ; x > 2 réponse E.   M8. L’inéquation x2 − x − 1 < 0 a pour ensemble de solutions : Solutions de x2-x-1=0 ; D = (-1)2 +4 =5. x = (1±5½) / 2. Le coefficient de x2 étant positif, l'ensemble des solution est ] (1-5½) / 2 ; (1+5½) / 2 [ réponse D. 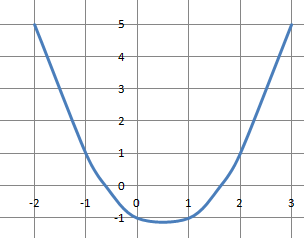M9. La somme des solutions distinctes de l’équation suivante vaut : x > 0. 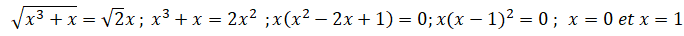Réponse E. L1. Donner sans justification l’ensemble des solutions de l’inéquation 1/(x+1) > -1. x doit être différent de -1 et 1 > -x-1 ; 2 > -x ; x > -2. ]-2 ; -1[ union ]-1 ; +oo[.  M10 Soit x et y deux nombres réels. Sachant que x − y > y et x + y < y, on peut affirmer que : x > 2y  et x < 0 ;  y < 0,5 x et x < 0 ; x < 0 et y < 0, réponse A . M11 Vrai ou faux ? L’inéquation ex > x2023 + 5 a une infinité de solutions réelles. Vrai. ex > 0 et  x2023 + 5 < 0 si x < -2. M12 Pour tout choix des nombres réels x, y, et z, le nombre x3 + y3 + z3 est égal à : A −3xyz + (x + y + z)(x2 + y2 + z2 − xy − yz − zx). Faux. −3xyz +x3+xy2+xz2-x2y-xyz-x2z+x2y+y3+yz2-xy2-zy2-xyz+x2z+y2z+z3-xyz-yz2-xz2. B −xyz xyz + (x + y + z)(x2 + y2 + z2 − xy − yz − zx). Faux C xyz xyz + (x + y + z)(x2 + y2 + z2 − xy − yz − zx). Faux D 3xyz + (x + y + z)(x2 + y2 + z2 − xy − yz − zx). Vrai +3xyz +x3+xy2+xz2-x2y-xyz-x2z+x2y+y3+yz2-xy2-zy2-xyz+x2z+y2z+z3-xyz-yz2-xz2. E aucune des autres réponses proposées M13 Soit a et b deux nombres réels tels que l’égalité suivante soit vraie pour tout réel x différent de 1 et 2. 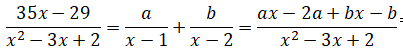Alors, a + 2b vaut : On identifie 2a+b = 29 et a+b = 35. a = -6 ; b =41 ; a+2b =76. Réponse E. L2. Donner sans justification les triplets (x, y, z) d’entiers naturels non nuls vérifiant simultanément les relations zx = y2x , 2z = 2x et x + y + z = 10. 2z = 2x conduit à x = z. zx = (y2)x conduit à z = y2. 2y2 +y -10= 0 ; D = 12 +80 = 81 = 92. y = (-1 ±9) / 4 ; soit y = 2 et y = -2,5. (4 ; 2 ; 4) et ( 6,25 ; -2,5 ; 6,25).  M14 Le nombre de solutions de l’équation ex = x + 1 est : réponse E ( une seule solution ). 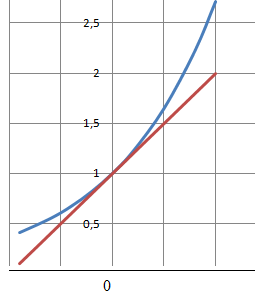Soit la fonction f(x) = ex ; f '(x) = ex ; f "(x) = ex >0, la fonction f(x) est convexe. Equation de la tangente en x =0 : y = f '(0) + b = x+b. Le point de coordonnées (0 ; 1) appartient à la tangente : 1 =b. y = x+1. La fonction étant convexe, son graphe se situe au dessus des ces tangentes, en particulier la tangente en x =0. ... .... Calculs de dérivées. M30. La dérivée de la fonction qf(x)= −1 /x +ln(x) est : f '(x) = 1 /x2 +1/x =(1+x) / x2. Réponse D. M31 La dérivée de la fonction f(x)= (x2 + 1) ln(x) est : On pose u = 1+x2 et v = ln(x) ; u' =2x ; v' = 1/x. u'v +v'u = 2x ln(x) +(x2+1) / x . Réponse E. M32. La dérivée de la fonction f(x)=(2+x) / (2-x) est égale à : on pose u = 2+x et v = 2-x ; u' =1 ; v' = -1. (u'v-v'u) / v2 =(2-x+2+x) / (2-x)2=4 / (2-x)2. Réponse E.   M33 à 35 Sur ]-oo ; 2 [ union ]2 ; +oo[, la fonction f(x) = (2+x) / (2-x) est : A. décroissante ;  B. croissante vrai ; C. ni croissante ni décroissante. La dérivée est strictement positive, la fonction est strictement croissante. M36. La dérivée de la fonction f(x)=ln(1+x2) est égale à : On pose u = 1+x2 ; u' = 2x ; f(u) = ln(u) ; f '(u) = u' /u ; f '(x) = 2x / (1+x2). Réponse B. M37. La dérivée de la fonction f(x)=exp(ex) est égale à : On pose u = ex ; u' = ex ; f(u )=eu ; f '(u) = u' eu ; f '(x) = ex exp(ex)) =exp(x+ex). Réponse A. M38. La dérivée de la fonction f(x)=x½ exp(x½) , x strictement positif, est égale à : On pose u = x½ ; u ' = ½x-½ ; v = exp(x½) ; v' =  ½x-½ exp(x½)  ; u'v+v'u =  ½x-½ exp(x½)+½ exp(x½)=½ exp(x½)(1+x-½ ). Réponse B.   L6. La dérivée de la fonction f(x)=ln[1+1/(1+2x)½] est égale à : M60 La dérivée troisième de la fonction f définie sur ]−∞, 1[ par f(x) = 3 ln(1 − x) est : On pose u = 1-x ; u' = -1 ; f(u) = 3 ln(u) ; f '(u) = 3 u' / u ; f '(x) = -3/(1-x). On pose v =( 1-x)  ;v '=-1 ; f '(v) = -3 / v ; f ''(v) = -3v ' / v2=3/ (1-x)2. On pose w = (1-x)2 ; w' = -2(1-x) ; f ''' (w) = -w' / w4 ; f '''(x) = -6  (1-x)3. Réponse A. M61 Soit n un entier naturel supérieur ou égal à 2. La dérivée seconde de la fonction f définie sur R par f(x) = xn est : f '(x) = n xn-1 ; f ''(x) = n(n-1) xn-2. Réponse C. M62 Soit n un entier naturel supérieur ou égal à 1. La dérivée n-ième de la fonction définie sur R par f(x) = xn est: n(n-1)(n-2)...* 2 =n !. Réponse E. M63 Soit n un entier naturel. La dérivée (n+1)-ième de la fonction f définie sur ]−∞, 1[ par f(x) = −ln(1−x) est : On pose u = 1-x ; u' = -1  ; f '(u) = -u'/ u ; f '(x) = 1/ (1-x). On pose v = 1-x ; v ' =-1 ; f ''(v) = -v'/ v2 ; f ''(x) = 1/ (1-x)2. On pose w = (1-x )2; w ' =-2(1-x) ; f '''(w) = -w'/ w2 ; f '''(x) = 2/ (1-x)3. On pose z = (1-x )3; z ' = -3(1-x)2 ; f (4)(z) = -z'/ z6 ; f (4)(x) = 2*3/ (1-x)4. f(n+1)(x)=n! / (1-x)n+1. Réponse C. M64 Si g est polynomiale de degré n alors :  g(k) est polynomiale de degré n − k pour tout entier k compris entre 0 et n. Réponse A. M65. La fonction exponentielle est-elle polynomiale ? Non. La dérivée n-k ième de ex est égale à g(n-k)=ex, différent d'une fonction polynomiale de degré n-k.

menu