Mathématiques, DNB Amérique du Nord 2023.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

.
. . .

.
.
.. ..
......


...
Exercice1. (20 points).
Les cinq situations suivantes sont indépendantes.
Situation 1 Décomposer en produit de facteurs premiers le nombre 780. Aucune justification n’est attendue.
780 =22 x 3 x 5 x13.
 Situation 2 On rappelle qu’un jeu de 32 cartes est composé de quatre familles (trèfle, carreau, cœur, pique). Chaque famille est composée de huit cartes : 7, 8, 9, 10, valet, dame, roi et as. L’expérience aléatoire consiste à tirer une carte au hasard dans ce jeu de 32 cartes.
a. Quelle est la probabilité d’obtenir le 8 de pique ? Aucune justification n’est attendue.
1 / 32.
 b. Quelle est la probabilité d’obtenir un roi ou un cœur ? Aucune justification n’est attendue.
7, 8, 9, 10, valet, dame, as et les 4 rois : 11 / 32.
 Situation 3 Développer et réduire l’expression A = (2x +5)(3x −4).
A = 6 x2-8x+15x-20=6 x2+7x-20.
Situation 4 a. Quel est le volume, en cm3 , de ce prisme droit ?
 b. Convertir ce résultat en litre. Rappel : 1 L = 1 dm3 .

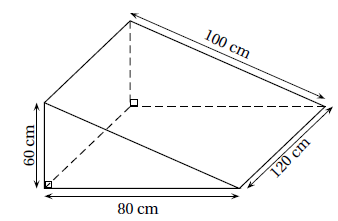
Aire du triangle de base : 60 x80 / 2 =2400 cm2.
Volume = aire de base  fois hauteur = 2400 x120 =288 000 cm3 = 288 dm3 = 288 L.

Situation 5
Le polygone 2 est un agrandissement du polygone 1.
Le coefficient de cet agrandissement est 3.
L’aire du polygone 1 est égale à 11 cm2.
Quelle est l’aire du polygone 2 ?
Aire du polygone1 fois 32 =11 x9 = 99 cm2.

Exercice 2 22 points
On considère la figure ci-contre. On donne les mesures suivantes :
AN = 13 cm ;  LN = 5 cm ; AL = 12 cm ; ON = 3 cm
 O appartient au segment [LN]
 H appartient au segment [NA]

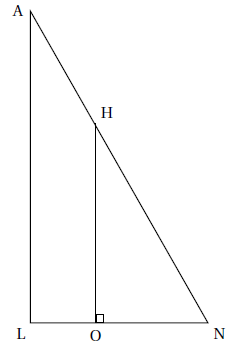1. Montrer que le triangle LNA est rectangle en L.
AN2 =132 = 169.
AL2+LN2=122 +52 = 144 +25 =169.
d'après la réciproque du théorème de Pythagore, le triangle LNA est rectangle en L.
2. Montrer que la longueur OH est égale à 7,2 cm.
D'après le théorème de Thalès : AL / OH = AN / HN = LN / ON = 5 /3.
OH = 3AL / 5 = 3 x 12 / 5 =7,2 cm.
3. Calculer la mesure de l’angle LNA. Donner une valeur approchée à l’unité près.
tan (LNA) = AL / LN = 12 /5 =2,4 ; cet angle mesure environ 67°.
4. Pourquoi les triangles LNA et ONH sont-ils semblables ?
Ils possèdent chacun un angle droit et l'angle (LNA) est commun. Ils sont donc semblables.
5. a. Quelle est l’aire du quadrilatère LOHA?
Aire d'un trapèze = (AL+HO) xLO / 2 = (12 +7,2) x2 / 2 = 19,2 cm2.
b. Quelle proportion de l’aire du triangle LNA représente l’aire du quadrilatère LOHA?
Aire du triangle LNA : AL x LN / 2 = 12 x5 / 2 =30 cm2.
19,2 / 30 = 192 /300 =32 /50 =16 /25.

Exercice 3 20 points
Les deux parties sont indépendantes
Partie A : évolution du nombre de visiteurs sur un site touristique
1. Le diagramme ci-dessous représente le nombre de visiteurs par an de 2010 à 2021 sur ce site.

a. Quel a été le nombre de visiteurs en 2010? Aucune justification n’est attendue.
300 000.
b. En quelle année le nombre de visiteurs a-t-il été le plus élevé? Aucune justification n’est attendue.
2019.
2. Le tableau ci-dessous indique le nombre de visiteurs sur le site touristique de cette ville en 2020 et en 2021 :
Année 2020  : 187 216 visiteurs.
Année 2021 : 219 042 visiteurs.
Le maire de cette ville avait pour objectif que le nombre de visiteurs progresse d’au moins 15% entre 2020 et 2021.
L’objectif a-t-il été atteint ?
219 042 -187 216 = 31 826.
31 826 / 187 216 ~17 %, l'objectif est atteint.

Partie B : étude des prix des hôtels de cette ville
Sur une période donnée, on relève les prix facturés pour une nuit par les hôtels de cette ville.
Prix facturés pour une nuit (en euro) 60
 80
 85
 90
 110
 120
 350
 500
Effectif
 1200
 1350
 1000
 1100
 1200
 1300
 900
 300
3. Déterminer l’étendue des prix facturés.
500 -60 = 440.
4. Quelle est la moyenne des prix facturés pour une nuit ? Arrondir à l’euro près.
(60 x1200 +80 x1350 + 85 x1000 + 90 x1100 +110 x1200 + 120 x 1300 +350 x900 +500 x300) / 8350 ~ 134 €.
5. L’association des hôteliers de cette ville cherche à attirer des touristes et annonce :
« Dans les hôtels de notre ville, au moins la moitié des nuits est facturée à moins de 100 €. Est-ce vrai ?
1200 + 1350 +1000 +1100 = 4650.
8350 / 2 =4 175.
4650  <  4 175. Donc c'est vrai.

.
.
....

 Exercice 4 20 points
À l’aide d’un logiciel de programmation, on veut réaliser lemotif « Fleur »suivant.

1. a. Le parallélogramme KLMN ci-dessous représente un des pétales du motif «Fleur ».
Construire ce parallélogramme sur la copie en prenant 1 cm pour 5 pas.

b. On définit le bloc « Pétale » ci-contre afin de dessiner ce parallélogramme.
On commence la construction du parallélogramme au point K en s’orientant vers la droite.
Par quelles valeurs doit-on compléter les lignes 4, 5, 6, et 7 du bloc « Pétale »?

2. Le bloc ci-dessous permet de construire un motif « Fleur » en partant de son centre.
a. Par quelle valeur doit-on compléter la ligne 2 du bloc « Fleur » ci-dessus ?

b. Expliquer le choix de la valeur « 72 » dans la ligne 4.
Le motif compte 5 pétales et on effectue une rotation de 360 / 5 =72°.
Après avoir tracé chaque pétale, on tourne de 72°.
c. On modifie le bloc « Fleur » pour construire le motif suivant :

Quelles sont alors les modifications à apporter aux lignes 2 et 4 du bloc « Fleur »?
Ligne 2 : répéter 12 fois ; ligne 4 : tourner de 30°.

Exercice 5 18 points
Un hippodrome est un lieu où se déroule des courses de chevaux. On s’intéresse à la piste d’un hippodrome.
Cette piste est composée de :
 deux lignes droites modélisées par des segments de 850 mètres ;
deux virages modélisés par deux demi-cercles de rayon 40 mètres.
Schéma de la piste de cet hippodrome.

1. Montrer que la longueur d’un tour de piste est d’environ 1 951 m.
850 +850 +3,14 x80 ~1 951 m.
2. Un cheval parcourt un tour de piste en 2 min 9 s.
a. Calculer la vitesse moyenne de ce cheval sur un tour de piste en mètre par seconde (m/s). Donner une valeur approchée à l’unité près.
1951 / ( 2 x60 +9)~15 m /s.
b. Convertir cette vitesse en kilomètre par heure (km/h).
15 x 3,6 =54 km / h.
3. On admet que la surface de la piste a une aire d’environ 73 027 m2.
On souhaite semer du gazon sur la totalité de la surface de la piste.
On doit choisir des sacs de gazon à semer parmi les trois marques ci-dessous :
A : 500 m2 couvert par sac ; prix d'un sac : 141,95 €.
B : 400 m2 couvert par sac ; prix d'un sac : 87,90 €.
C : 300 m2 couvert par sac ; prix d'un sac : 66,50 €.
Quelle marque doit-on choisir pour que cela coûte lemoins cher possible?
A : 73 027 / 500 =146 sacs soit 146 x141,95 ~20 725 €.
B : 73 027 / 400 ~183 sacs soit 183 x 87,9 ~16 086 €.
C : 73 027 / 300 =244 sacs soit 244 x 66,5 ~13 226 €.
La marque B est retenue.

  
menu