Exercice 1 10 points

Lorsqu’un tiroir se referme, le fond du tiroir, marqué par le point M, se rapproche du fond du meuble, marqué par le point O.
On note f (t ), la distance entre le point O et le point M, à l’instant t .
f (t ) est exprimée en centimètres et t est exprimée en seconde.
L’instant t = 0 correspond au moment où l’utilisateur pousse le tiroir pour le fermer.
Les deux parties peuvent être traitées de façon indépendante
Partie A. Résolution d’une équation différentielle.
On admet que la fonction f est solution de l’équation différentielle :
(E
0) : y′′+5y′+4y = 0,
où y est une fonction inconnue de la variable réelle t , définie et
deux fois dérivable sur [0 ; +∞[, et où y′ est la dérivée de y , et y′′
la dérivée seconde de y.
1. a. Résoudre l’équation : r
2+5r +4 = 0.
Discriminant : 5
2-4*4=9=3
2.
Solutions : r
1 = (-5+3) / 2 = -1 ;
r2 = (-5-3) / 2 = -4.
b. Résoudre l’équation différentielle (E
0).
f(t) = A exp(-t) + B exp(-4t) avec A et B des constantes.
2. On suppose qu’à l’instant t =0, la situation est la suivante :
- le point M est situé à 20 cm du point O.
- le point M se déplace vers le point O avec une vitesse négative égale à −10 cm·s
−1.
a. En déduire la valeur de f (0) et celle de f ′(0).
f(0) = A +B = 20.(
1)
f '(t) = -A exp(-t) -4B exp(-4t).
f '(0) = -A-4B= -10. (
2).
(
1)+(
2) donne : -3B=10 ; B = -10 /3 et A = 70 / 3.
b. On admet que :
f (t )=70 / 3 exp(-t) -10/ 3exp(-4t).
Déterminer la valeur exacte de la distance OM, deux secondes après le début de la fermeture.
f(2) = 70 /3 e
-2-10 / 3 e
-8.
Le tiroir est dit fermé lorsque la distance OM est inférieure à 0,5 cm.
Le constructeur affirme que le tiroir est fermé en moins de 4 secondes. A-t-il raison? Justifier.
f(4)=
70 /3 e-4-10 / 3 e-16~0,43 cm < 0,5 cm. Il a raison.
Partie B. Étude de fonction
On considère à nouveau la fonction f définie sur l’intervalle [0 ; +∞[ par :
f (t )=70 / 3 exp(-t) -10/ 3exp(-4t).
On admet que la fonction f est dérivable et on note f ′ sa fonction dérivée.
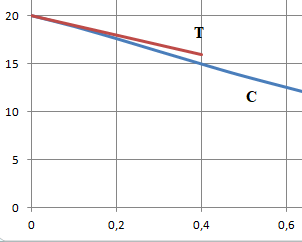
On note C la courbe représentative de la fonction f .
1. a. Déterminer la limite de f(t) en plus l'infini.
En +oo, e-t et e-4t tendent vers zéro ; f(t) tend vers zéro.
b. En déduire que la courbe C possède une asymptote dont on donnera une équation.
L'axe des abscisses (y=0) est asymptote à la courbe C.
2. a. Déterminer f ′(t ) pour tout t appartenant à [0 ; +∞[.
f '(t) = -70 /3 e-t +40 / 3e-4t.
b. On admet que sur l’intervalle [0 ; +∞[ on a f ′(t ) < 0.
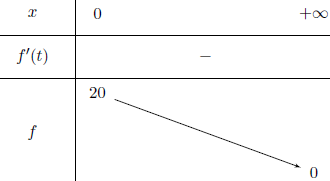
En déduire le tableau de variations de la fonction f sur l’intervalle [0 ; +∞[.
3. On considère l’algorithme suivant :
t←0
p←0,1
s←0,5
Tant que (70/3)* eˆ(- t) - (10/3)*eˆ(- 4t) > s
t←t + p
Fin Tant que.
a. Recopier le
tableau ci-dessous, au besoin en rajoutant des lignes, et compléter à
partir de la ligne numéro 36 jusqu’a ce que l’algorithme s’arrête.
ligne
|
t
|
valeur de f(t) arrondie à 0,01
|
Condition
(70/3)* eˆ(- t) - (10/3)*eˆ(- 4t) > s
|
0
|
0
|
20
|
vraie
|
1
|
0,1
|
18,88
|
vraie
|
2
|
0,2
|
17,61
|
vraie
|
|
|
|
|
36
|
3,6
|
0,64
|
vraie
|
37
|
3,7
|
0,58
|
vraie
|
38
|
3,8
|
0,52
|
vraie
|
39
|
3,9
|
0,47
|
fausse
|
b. Quelle est la
valeur de la variable t à la fin de l’exécution de l’algorithme ?
Interpréter le résultat dans le contexte de l’exercice.
t = 3,9 s. Le tiroir est fermé au bout de 3,9 s.
4. On note T la tangente à la courbe C au point d’abscisse 0.
Un logiciel de calcul formel donne la partie régulière du développement
limité à l’ordre deux de la fonction f au voisinage de zéro. f(t)
=20-10t-15t
2.
a. Déterminer une équation de la tangente T.
y = 20 -10 t.20-10
Les questions b. et c. sont des questions à choix multiples. Une seule réponse est exacte.
Recopier sur la copie la réponse qui vous parait exacte. On ne demande aucune justification.
b. Le développement limité de f à l’ordre deux au voisinage de zéro est :
20-10t-15t
2+t
2e(t) avec limite de
e(t) = 0.
c. On s’intéresse à la position de la courbe C par rapport à la tangente T au voisinage de 0.
On peut affirmer que la courbe C est en dessous de la tangente T.