Exercice 1. 10 points
Les deux parties de l’exercice peuvent être traitées indépendamment
Afin de vérifier la bonne isolation thermique d’un spa, on porte la
température de l’eau, du spa à 38 °C puis on coupe l’alimentation
électrique du spa qui sert à chauffer l’eau.
On s’intéresse a l’évolution de cette température en fonction du temps écoulé à partir de cette coupure.
La température de l’eau du spa est modélisée par une fonction f qui, à
tout temps t (en heures) écoulé depuis la coupure de l’alimentation
électrique, associe la température f (t ), en degré Celsius (°C), de
l’eau du spa au temps t .
On admet que f (0) = 38.
Lors de cette vérification, la température ambiante extérieure au spa
reste constante et égale à 25 °C. On remarque que la température de
l’eau du spa est de 37 °C au bout de 1,5 h.
Partie A.
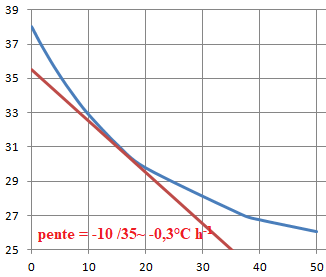
On a tracé la représentation graphique C de la fonction f dans un
repère orthogonal. On utilisera cette représentation graphique pour
répondre aux questions de cette partie.
 1.
1. Donner la valeur
arrondie, au degré Celsius, de la température de l’eau du spa 22 heures
après la coupure de l’alimentation électrique. Faire apparaître les
traits de construction correspondants sur le graphique
2. La température de l’eau du spa descend-elle en-dessous de 27 ° C ?
Si oui, combien de temps après la coupure de l’alimentation électrique ?
Au bout de 37 heures, la température est inférieure à 27 °C.
3. On admet que la
vitesse instantanée de variation de la température de l’eau du spa,
exprimée en degrés Celsius par heure (°C/h), à un temps donné t
0, est le coefficient directeur de la tangente à la courbe C au point d’abscisse t
0.
Pour chacune des deux propositions suivantes, indiquer si elle est vraie ou fausse. Justifier chaque réponse.
a. Proposition A : « toutes les heures, la température de l’eau du spa baisse du même nombre de degrés Celsius. »
Faux, les tangentes à la courbe C sont de moins en moins inclinées sur l'horizontale.
b. Proposition B : « la vitesse instantanée de variation de la température de l’eau du spa au temps t
0 =15 h est environ égale à −1 ° C/h. » Faux.
 Partie B
Partie B.
On admet que, pour tout réel t de l’intervalle [0 ; +∞[, f (t ) =13e
−0,05t +25.
1. Calculer la valeur arrondie à 10
−1 de f (24).
Interpréter cette valeur dans le contexte de l’exercice.
f(24)=13 exp(-0,05*24)+25 ~28,9°C.
Au bout de 24 heures, la température de l'eau est égale à 28,9°C.
2. a. Pour tout réel t de l’intervalle [0 ; +∞[, déterminer une expression de f ′(t ).
f '(t)= -13 x0,05 exp(-0,05t) = -0,65 exp(-0,05t).
b. En déduire le sens de variation de la fonction f sur l’intervalle [0 ; +∞[.
Ce sens de variation paraît-il cohérent avec le contexte de l’exercice ? Argumenter.
exp(-0,05t) > 0 ; f '(t) < 0 ; f(t) strictement décroissante.
Après coupure du chauffage, la température décroît jusqu'à 25 °C.
3. a. Déterminer la limite de la fonction f en +∞.
b. Interpréter la valeur de cette limite dans le contexte de l’exercice.
Le terme en exponentielle tend vers zéro et f(t) tend vers 25 °C.
Au bout d'un temps assez long, l'eau atteint la température de l'air ambiant.
4. Une alarme
sonore est émise quand la température de l’eau du spa devient
strictement inférieure à une température programmée par l’utilisateur.
a. L’utilisateur programme la température de l’eau du spa à 36 °C.
Déterminer, par le calcul, combien de temps après la coupure de l’alimentation électrique cette alarme sonore retentira.
On donnera la valeur exacte de cette durée, puis la valeur arrondie à la minute.
13 exp(-0,05 t) +25 = 36 ; exp(-0,05t) =(36-25) /13 =0,846.
-0,05 t = ln(
(36-25) /13) ; t =
ln((36-25) /13) /0,05 ~3,34 h ou 3 h 20 min.
b. Quelle est la valeur numérique affichée par l’algorithme ci-dessous ?
H ←0
T ←38
Tant que T >34
H ←H +1
T ←13e−0,05H +25
Fin du tant que
Afficher H.
c. Expliquer ce que cet algorithme permet de déterminer dans le contexte de l’exercice.
Cet algorithme calcule la durée ( en heure) au bout de laquelle la température de l'eau atteint 34°C.
Au bout de 7 h, T = 34,1°C. Au bout de 8 heures, T = 33,7 °C.