Mathématiques,
BTS 2023 Opticien lunetier.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Exercice 1. 10 points On s’intéresse à une entreprise qui commercialise des montures de lunettes.
Les quatre parties de cet exercice peuvent être traitées de façon indépendante.
Partie A - Etude d’une série statistique.
Le graphique ci-dessous représente l’évolution des ventes d’un modèle demonture de lunettes depuis l’année 2017.
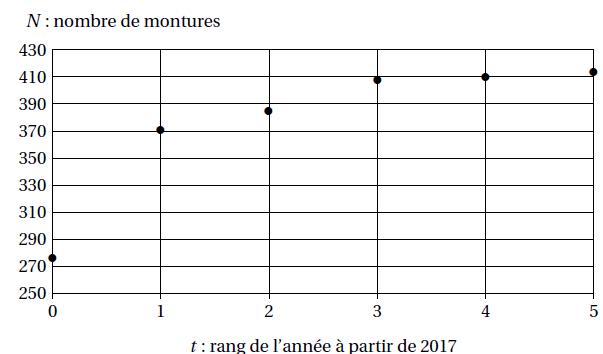 1.
1. Expliquer pourquoi un ajustement affine de N en t n’est pas pertinent.
Les points ne sont pas alignés.
2. On effectue le changement de variable z = ln(415−N).
On obtient alors le tableau suivant :
année
|
2017
|
2018
|
2019
|
2020
|
2021
|
2022
|
t
|
0
|
1
|
2
|
3
|
4
|
5
|
z
|
4,94
|
3,81
|
3,45
|
2,14
|
1,86
|
0,77
|
.a. A l’aide de la calculatrice, donner le coefficient de corrélation linéaire de la série (t ; z). Arrondir à 10 −3.
z= -0,800 t+4,829
b. Un ajustement affine de z en t est-il pertinent ? Justifier.
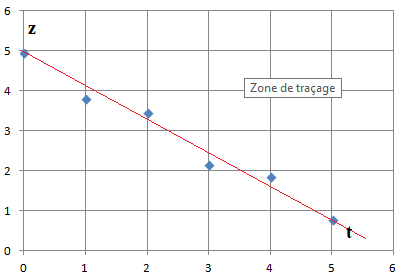
Les points sont à peu près alignés ; un ajustement affine de z en t est pertinent.
3. A l’aide de la
calculatrice, donner l’équation de la droite de régression linéaire de
z en t , selon la méthode des moindres carrés, sous la forme z = at +b.
Les coefficients a et b seront arrondis à 10 −2.
z= -0,800 t+4,829.
4. En déduire une expression de N à l’aide de t sous la forme :
N = 415−Ce−0,8t , où C est une constante que l’on déterminera, à l’unité près.
ln(415-N) =-0,800 t+4,829.
415-N = exp(-0,80t +4,829) = exp-0,8t) x exp(4,829) =125 exp(-0,8t).
N = 415-125 exp(-0,8t).
5. On suppose que l’évolution constatée se poursuit. Quel sera le nombre de montures vendues en 2023?
t =6 ; N =415-125 exp(-0,8 x6) ~414.
Partie B - Résolution d’une équation différentielle.
On considère l’équation différentielle :
(E) : 5y′ +4y = 1660,
où y est une fonction inconnue de la variable t , définie et dérivable
sur l’intervalle [0;+∞[ , et où y′ est sa fonction dérivée.
1. Déterminer les solutions de l’équation différentielle
(E0) : 5y′+4y = 0.
y = A exp(-0,8t) avec A une constante.
2. Soit c in nombre réel. On considère la fonction constante g , définie par g (t )= c.
Déterminer c pour que la fonction g soit solution de l’équation différentielle (E).
g'(t) = 0 ; 4 g(t) = 1660 ; g(t) = 415.
3. En déduire les solutions de l’équation différentielle (E).
y = Aexp(-0,8t) +415.
4. Déterminer la fonction f , solution de l’équation différentielle (E), qui vérifie la condition initiale f (0) = 290.
290 = A e0+415 ; A = 290-415=125.
Partie C - Étude d’une fonction.
On considère la fonction f , définie sur l’intervalle [0;+∞[ par : f (t ) = 415−125e−0,8t .
On admet que cette fonction modélise l’évolution du nombre de montures vendues en fonction du temps :
t désigne le temps écoulé, en années, à partir de l’année 2017.
f (t ) désigne le nombre de montures vendues.
On note C la courbe représentative de la fonction f .
1. On sait que la courbe C admet une asymptote en +∞. Donner une équation de cette asymptote.
Interpréter ce résultat dans le contexte de l’exercice.
En plus l'infini, exp(-0,8t) tend vers zéro et f(t) tend vers 415.
Au bout de quelques années, on vendra 415 montures.
Equation de l'asymptote : y = 415.
2. Déterminer le sens de variation de la fonction f sur l’intervalle [0;+∞[.
f '(t) = 125 x0,8e-0,8t > 0 ; f(t) est strictement croissante.
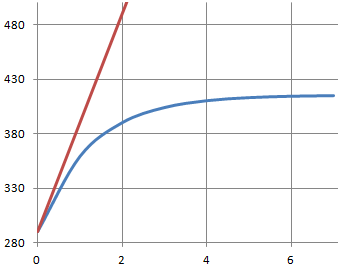
3. On note T la tangente à la courbe de C au point d’abscisse 0.
Indiquer, sans justifier, laquelle des trois situations ci-dessous
représente correctement la position de la courbe C par rapport à la
tangente T au voisinage de zéro.
f "(t) =-80 e-0,8t) < 0 ; la conction est concave ; la courbe C est en dessous de ces tangentes.
Partie D - Étude d’une suite.
On considère une suite (un) définie par u0 = 3000, et, pour tout entier naturel n : un+1 = 0,9un +500.
La suite (un) représente l’évolution du nombre de clients de l’entreprise.
Ainsi un correspond au nombre de clients durant l’année 2017+n.
1. Vérifier que le nombre de clients lors de l’année 2018 est égal à 3200.
u1=0,9 u0 +500=0,9 x 3000 +500= 3200.
2. Pour tout entier naturel n, on pose vn = un −5000.
Démonter que (vn) est une suite géométrique de raison 0,9.
vn+1 = un+1 −5000=0,9 un+500-5000=0,9un-4500=0,9(un-5000)=0,9 vn.
3. Exprimer, pour tout entier naturel n, le terme vn en fonction de n.
vn = v0 * 0,9n= -2000 x0,9n.
4. En déduire que, pour tout entier naturel n : un = 5000−2000×0,9n .
un = vn +5000 =5000−2000×0,9n .
5. Déterminer le nombre de clients lors de l’année 2023.
n =6 ; u6=5000-2000x0,96=3937.
6. On considère l’algorithme suivant :
n←1
u←3000
Tant que u< 4000
n←n+1
u←0,9*u+500
Fin Tant que
Quelle est la valeur de la variable n après l’exécution de l’algorithme ?
5000−2000×0,9n < 4000.
- 2000x0,9n < -1000 ; 0,9n > 0,5 ; n ln(0,9) > ln(0,5) ; n > ln(0,5) / ln(0,9) ; n > 6,57. n = 7.
A partir de 2017+7 = 2024, le nombre de clients sera supférieur à 4000.
|
| .
. |
....
|
Exercice 2 10 points
Partie A - Probabilités conditionnelles.
L’usine se procure des verres semi-finis auprès de trois fournisseurs différents.
• 30 % des verres semi-finis proviennent d’un premier fournisseur.
Parmi eux, 3 % sont défectueux.
• 60 % des verres semi-finis proviennent d’un deuxième fournisseur.
Parmi eux, 4 % sont défectueux.
• 10 % des verres semi-finis proviennent d’un troisième fournisseur.
Parmi eux, 2 % sont défectueux.
On prélève un verre semi-fini au hasard. On considère les événements suivants.
F1 : « le verre semi-fini provient du premier fournisseur »,
F2 : « le verre semi-fini provient du deuxième fournisseur »,
F3 : « le verre semi-fini provient du troisième fournisseur »,
D : « le verre semi-fini est défectueux ».
1. Recopier et compléter l’arbre de probabilités suivant :
2. Calculer la probabilité P (F1 ∩D).
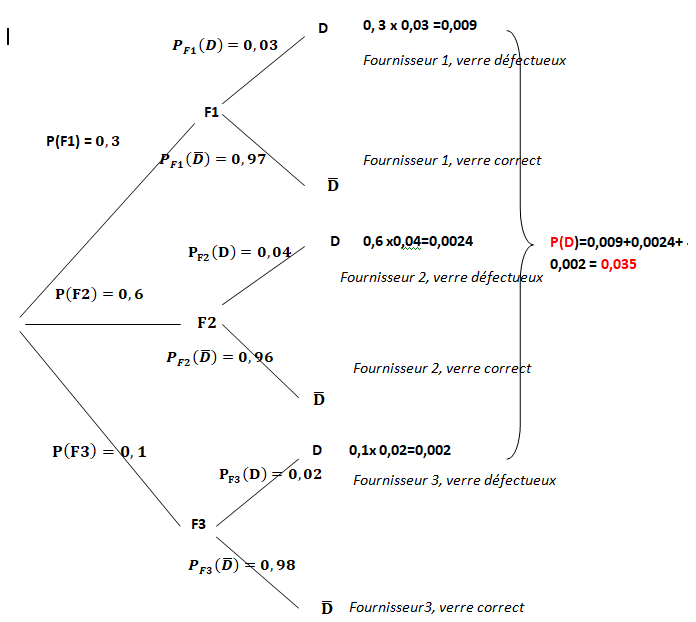
3. Montrer que la probabilité que le verre semi-fini soit défectueux est égale à 0,035.
4. On sait que le verre semi-fini est défectueux. Quelle est la probabilité qu’il provienne du premier fournisseur ?
PD(F1) = P(D n F1) / P(D)=0,009 / 0,035=0,257.
Partie B - Loi binomiale et loi normale.
On estime que 3,5 % des verres semi-finis du stock de l’usine sont défectueux.
On prélève un échantillon aléatoire de 200 verres semi-finis dans le stock de l’usine.
On considère la variable aléatoire X qui donne le nombre de verres semi-finis défectueux au sein de l’échantillon.
1. a. On admet que la variable aléatoire X suit une loi binomiale. Donner ses paramètres.
n=200 ; p =0,035.
b. Calculer la probabilité P(6 < X <10).
P(X < 5) =0,2961 ; P(X < 10) =0,9053 ;
P(6 < X <10)= 0,9053-0,2961=0,609.
2. On admet que
l’on peut approcher la loi de probabilité de la variable aléatoire X
par une loi normale d’espérance 7 et d’écart type 2,599.
a. Justifier la valeur de ces paramètres
E =np = 200 x0,035 =7 .
s = (np(1-p)½=(7 x 0,965)½ =2,599.
b. On considère une variable aléatoire Y suivant une loi normale d’espérance 7 et d’écart type 2,6.
Calculer P(5,5< Y < 10,5).
Interpréter dans le contexte.
P(Y < 10, 5) =0,911 ; P(Y < 5,5) =0,282 ;
P(5,5< Y < 10,5)= 0,911-0,282=0,629.
La probabilité qu'il y ait entre 6 et 10 verres défectueux est égale à 0,629.
Partie C - Loi exponentielle.
On s’intéresse au standard téléphonique de l’usine.
On considère T la variable aléatoire qui, à chaque appel au standard, associe le temps d’attente, en minutes.
On admet que T suit la loi exponentielle de paramètre l= 0,2.
1. Calculer l’espérance de la variable aléatoire T . Interpréter dans le contexte.
E = 1 / l = 1 /0,2 = 5.
Le temps d'attente est en moyenne de 5 minutes.
2. On considère un appel au standard, choisi au hasard.
Déterminer la probabilité que le temps d’attente correspondant à cet appel soit compris entre 2 et 4 minutes.
P(T < 4) - P(T < 2) = 1-exp(-0,2 x4)-(1-exp(-0,2 x2))=e-0,4 -e-0,8 =0,221.
Partie D - Estimation
L’usine souhaite estimer la proportion p de clients satisfaits d’un nouveau verre.
Sur un échantillon de 100 clients choisis au hasard, 80 d’entre eux ont déclaré être satisfaits.
1. Donner une estimation ponctuelle f de la proportion p.
f =80 /100 =0,80.
2. Donner une estimation de p par un intervalle de confiance avec le coefficient
de confiance 90 %.
On fournit la formule suivante :
Intervalle de confiance d’une proportion avec un coefficient de confiance de 90 %
[ f −1,65(f(1-f) / n)½ ; f +1,65(f(1-f) / n)½ ]
(f(1-f) / n)½ = (0,8 x0,2 / 100)½ =0,04 ; 1,65 x0,04 =0,066.
[0,8-0,066 ; 0,8 +0,066] soit [0,734 ; 0,866].
3. Déterminer les entiers naturels n vérifiant l’inégalité : 1,65(0,16 / n)½ < 0,03.
Interpréter le résultat dans le contexte.
(0,16 / n)½ < 0,03 / 1,65 =0,01818.
0,16 / n < 0,018182 =3,3058 10-4 ;
n > (0,16 / (3,3058 10-4).
n > 484.
Pour un intervalle de confiance à 90 % avec une marge d'erreur d'au
plus 3 points, l'échantillon doit contenir au moins 484 clients.
|
|