Corrigé
physique, face au miroir, un filet d'eau,
Concours CAPLP maths sciences 2023.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
B.1. Position du miroir plan.
Une personne qui se brosse les dents se tient face au miroir plan de la
salle de bain, fixé au-dessus du lavabo.
On notera :
d la distance de la personne au miroir ;
l la hauteur du miroir ;
A le sommet de la tête ;
O la position des yeux ;
B le bas du buste ;
P les pieds.
On supposera l’épaisseur du miroir plan négligeable.
13. Représenter
l’image A′B′ du buste AB donnée par le miroir.
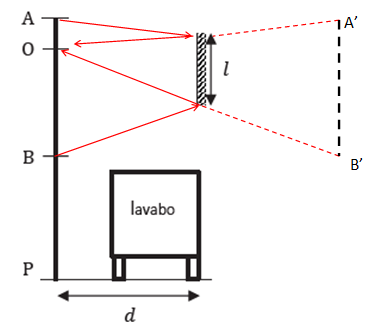
Afin
de déterminer géométriquement la position d'une image, il faut tracer,
à partir de l'objet, une droite normale à la surface du miroir. Le
point image se trouve sur cette droite, à la même distance du miroir
que le point objet correspondant.
14. Déterminer l’expression
littérale de la hauteur l du miroir pour que la personne ne voie que
son buste AB.
Les rayons réfléchis par le miroir doivent passer par l'oeil O.
l = ½AB.
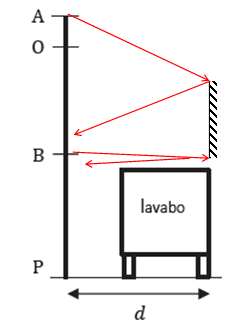
15. Préciser si
l’on peut accrocher le miroir à n’importe quelle hauteur à partir du
sol.
Non, les rayons issus de A et B, réfléchis par le miroir, ne passeront
pas tous par l'oeil.
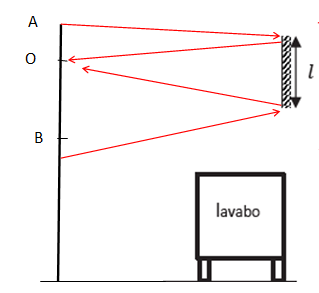
16. Indiquer si la
personne peut voir une partie plus importante de son corps si elle
recule.
Oui
B.2. Utilisation d’un
miroir de maquillage.
L’utilisateur du miroir souhaite observer plus en détail l’une de ses
dents.
Cette dent est considérée comme un objet réel AB.
17. Rappeler en
quoi consiste l’approximation de Gauss.
L'approximation de Gauss consiste à considérer des rayons paraxiaux (
angle d'incidence faible).
18.
Préciser si la personne doit utiliser un miroir concave ou un miroir
convexe pour observer cette dent droite et agrandie. Pour répondre à la
question, effectuer le tracé des rayons en faisant figurer au
moins deux rayons particuliers sur chaque exemple proposé. On notera AB
la dent-objet et A′B′ l’image de cette dent donnée par le miroir.
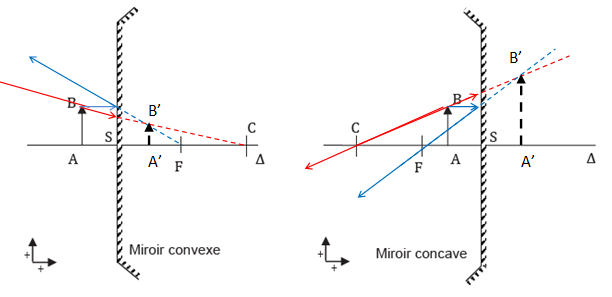
19. On note R le
rayon de courbure du miroir. Donner la valeur du rayon de courbure du
miroir grossissant avec l’incertitude-type associée.
On prendra pour la suite du problème R = mesure algébrique SC = −0,80 m.
mesure
algébrique SA
|
mesure
algébrique SA' |
1/
mes alg SA
|
1/
mes alg SA'
|
2/
mes alg SC
|
mes alg SC
|
-1,65
|
-0,529
|
-0,606
|
-1,89
|
-0,606-1,89=-2,496
|
-0,8012
|
-1,55
|
-0,551
|
-0,645
|
-1,815
|
-2,46
|
-0,813
|
-1,45
|
-0,567
|
-0,690
|
-1,764
|
-2,453
|
-0,815
|
-1,35
|
-0,582
|
|
|
-2,459
|
-0,813
|
-1,25
|
-0,594
|
|
|
-2,483
|
-0,805
|
-1,15
|
-0,625
|
|
|
-2,47
|
-0,81
|
-1,05
|
-0,654
|
|
|
-2,48
|
-0,806
|
-0,95
|
-0,704
|
|
|
-2,473
|
-0,809
|
Valeur moyenne
de R : 0,81 ±0,08 m
L’oeil emmétrope peut accommoder à des distances allant du punctum
proximum dpp à l’infini. On
supposera que la position de l’oeil est confondue avec celle de la dent
observée et est sur l’axe optique.
20. Déterminer la
distance SA1 ̅̅̅̅ pour que l’image de la dent soit à
l’infini.
Image à l'infini : 1/ mes alg SA1 = 2 / mes alg SC =2/
(-0,80) ; mes alg SA1 = -0,40 m.
21. Déterminer la
distance SA2 ̅̅̅̅̅ pour que l’image de la dent soit au
punctum proximum de l’oeil, droite
et agrandie. On considèrera que A2A'2 = dpp
= 25,0 cm.
A2S+SA'2 = 0,25 ; SA'2 = 0,25 -A2S.
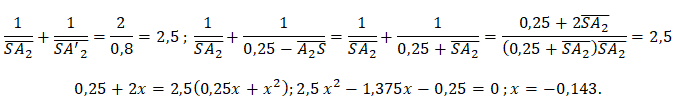 La latitude de
mise au point correspond à l’intervalle des positions de
l’objet par rapport au miroir qui donnent une image nette pour
l’observateur.
La latitude de
mise au point correspond à l’intervalle des positions de
l’objet par rapport au miroir qui donnent une image nette pour
l’observateur.
22. Déduire des
questions précédentes la latitude de mise au point associée à ce miroir.
0,40-0,143=0,257 m.
|
...
|
....
|
Partie D : un filet d’eau.
Une fois les dents brossées, la personne remplit un verre d’eau pour se
rincer la bouche. Lorsque le robinet est ouvert, elle s’aperçoit que le diamètre du filet d’eau
diminue à partir de la sortie.
Ce filet est vertical, à l’air libre (pression extérieure P0) et possède une symétrie de révolution autour d’un axe descendant O de vecteur unitaire ez. On note r son rayon après une hauteur z de chute depuis l’origine du filet située au point O.
On néglige dans toute cette partie le phénomène de tension
superficielle et on se place en régime stationnaire.
38. L’écoulement d’eau est supposé incompressible. Préciser la
conséquence de cette hypothèse sur le débit volumique Dv.
Le débit volumique reste constant.
39. Proposer un protocole expérimental permettant d’accéder à la valeur
numérique du débit volumique associé au filet d’eau.
Faire couler l'eau dans une grande éprouvette graduée et relever le volume à intervalles de temps réguliers.
40. Déterminer un ordre de grandeur du nombre de Reynolds pour
l’écoulement étudié. En déduire si ce sont les effets de la viscosité ou ceux de
la convection qui prédominent dans cet écoulement.
Re = r V L / h.
r = 1000 kg m-3 ; débit volumique Dv= 8,6 10-6 m3 s-1 ; viscosité dynamique de l'eau 10-3 Pa s.
V = Dv / (pr02)=8,6 10-6 /(3,14 x25 10-6)~0,11 m /s.
L = grandeur caractéristique, section du jet. V : vitesse.
Dv = V L.
Re = 103 x 8,6 10-6 / 10-38,6.
Re < 2000 et les lignes de courant sont pratiquement des droites. L'écoulement est laminaire.
Re étant petit, la viscosité est dominante.
L’écoulement de l’eau est supposé parfait et son champ des vitesses
vérifie l’équation d’Euler :
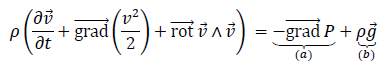
41. Définir un « écoulement parfait ».
L'écoulement est parfait si les forces de viscosité sont nulles. Les
forces de contact se réduisent aux forces de pression. Il n'y a pas de
déperdition d'énergie dans le fluide qui se déplace.
42. Donner la signification des termes (a) et (b) qui apparaissent dans l’équation d’Euler.
(a) : force de pression ; (b) : force de pesanteur.
On considère une ligne de courant quelconque de l’écoulement reliant deux points A et B ; le
déplacement élémentaire dl le long d’une telle ligne est colinéaire au vecteur vitesse.
43.
En intégrant l’équation d’Euler le long de cette ligne de courant,
retrouver la relation de Bernoulli pour un écoulement parfait,
stationnaire, incompressible et homogène dans le champ de pesanteur
uniforme :
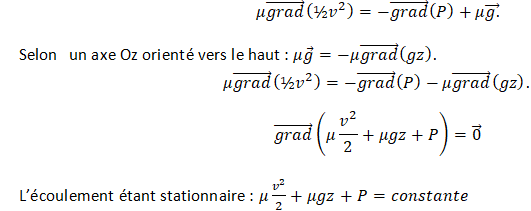
½vA2 -gzA +PA / µ =½vB2 -gzB +PB / µ .
Le champ des vitesses du filet d’eau est dorénavant approché par la forme 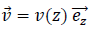 (toute (toute
composante
horizontale de la vitesse est négligée, ainsi que la non uniformité
éventuelle de sa valeur sur n’importe quelle section de l’écoulement).
4. Montrer à partir de la relation de Bernoulli précédente, et sachant que la pression est continue à l’interface eau-air, que :
v(0)2 = v(z)2 − 2gz.
PA = PB ; ½vA2 -gzA =½vB2 -gzB .
½v02 -gz0 =½v(z)2 -gz .
½v02 =½v(z)2 -g(z-z0)=½v(z)2 -gz.
v(0)2 = v(z)2 − 2gz.
45. Déterminer l’expression de 1/r4 en fonction de z, g, Dv et du rayon initial r0 du filet d’eau.
v(z) x pr2 = Dv ;
v(0)2 =Dv2 / (p2r04)= Dv2 / (p2r4)− 2gz.
1/(p2r04)= 1 / (p2r4)− 2g / Dv2 z.
1/r04= 1 / r4− 2g p2 / Dv2 z.
1 / r4= 2g p2 / Dv2 z+1/r04.
Le document 6 propose un traitement des mesures expérimentales en considérant la représentation de 1/r4
en fonction de z : au nuage des points expérimentaux est superposée une
régression affine et le tracé des résidus (ou écarts) normalisés est
fourni.
46. Discuter l’accord de la loi obtenue à la question précédente avec l’expérience du document 6.
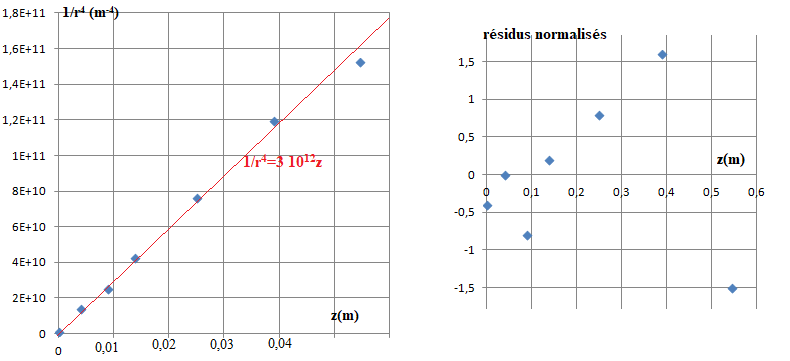
Les résidus sont assez bien distribués symétriquement.
Les 5 premiers sont inférieurs à 1.
Leur moyenne est proche de zéro.
La loi obtenue et les résultats de l'expérience sont en acord.
|
|